高斯噪聲實時產生算法及在ADSP-TS201S上的實現

李 偉, 楊 斌

(西南交通大學信息科學與技術學院,四川成都610031)

1 引言

隨機噪聲在通信等過程中往往是有害并需設法消除的無用信號,然而在一些情況下,也需要人為產生噪聲,如自適應控制系統、系統辨識等領域。正態分布的高斯噪聲是最常用的一種噪聲。隨機噪聲由隨機數表達,因此隨機噪聲的產生就歸結于隨機數的產生問題。由隨機信號理論可知,在(0,1)上服從均勻分布的隨機數經過一定的變換,可產生服從N(0,1)正態分布的高斯隨機數[1]。

隨機數的產生大致可分為查表法、物理法(如真空管射槍噪聲)、數學遞推法[2]。計算機產生隨機數用到的是數學遞推法,字長和精度有限的計算機或DSP產生真正的隨機數是不可能的,因而現有的隨機數產生算法產生的隨機數均是偽隨機數,即所得隨機數都有一定的周期性。實際應用中也不必采用真正隨機的數,達到一定程度隨機性的偽隨機數就可以滿足一般要求了。

文中介紹了3種產生(0,1)均勻分布隨機數的算法,隨后介紹了2種用(0,1)均勻分布隨機數生成正態分布隨機數的快速生成方法,最后在ADSP-TS201S上實現了實時高斯噪聲生成算法,能以10kHz的頻率連續產生兩路2048對不重復的正交高斯噪聲數據。

2 均勻分布隨機數的產生

均勻分布隨機數產生的算法很多,如乘同余法、線性同余法、移位寄存器法、迭代取中法、加同余法、二次剩余法、進位加/借位減/進位乘(AWC/SWB/MWC)發生器法[3]等。根據實時性要求,主要介紹3種相對產生隨機數速度較快的算法,3種算法產生的隨機數均在(0,2L)區間上服從均勻分布,結果除以常數2L,即可得到(0,1)均勻分布的隨機數。

2.1 乘同余法

乘同余法用如下的遞推同余式產生隨機序列：

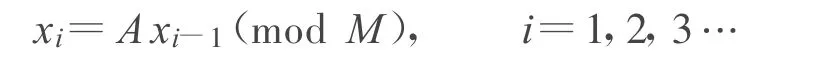
其中,xi為當前隨機數,xi-1為前一時刻隨機數;M為模值,取2的冪,即 M=2L,L＞2的整數;A為乘因子,一般取小于M 且模8等于3或5的奇數;初值 x0取0～2L之間任意奇數。可以證明,該算法產生的隨機數序列的周期為2L-2[2]。

2.2 線性同余法

線性同余法又稱為混合同余法,遞推公式如下：

這是一種類似乘同余的算法,只多了個增量c。根據隨機數理論,A的后3位一般為“偶數-2-1”形式,如421、821等;初值 x0取0～2L之間任意奇數;Coveyou給出增量c滿足的一個等式可以在 A取值不大的條件下,有效地減小序列的相關系數,而且不占用過多的機器時間。用該方法產生的隨機序列的周期為2L[1]。

2.3 移位寄存器法

這是一種基于m序列理論的算法,可以利用線性反饋移位寄存器(LFSR)產生隨機序列。根據m序列本原特征多項式,采取合適的回饋,M級LFSR產生的隨機數的最大周期為2M-1。M階m序列本原特征多項式可以表示為：

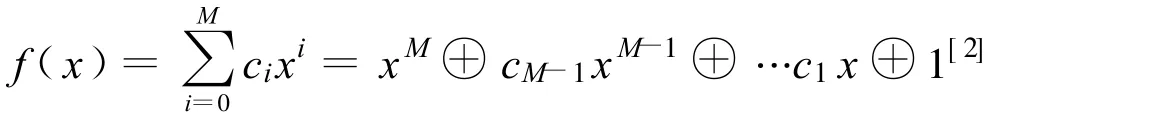
⊕表示模2或者異或運算,系數ci取0或1,轉化為最大周期LFSR就是根據系數在LFSR相應位抽頭。例如(16,12,3,1,0)表示16級LFSR的本原特征多項式為：

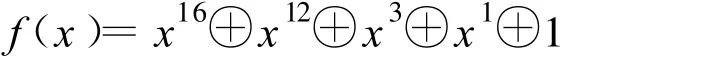
則應在LFSR16、12、3、1位抽頭,如圖1所示。每次移位運算后,把整個的16位數作為隨機數輸出。同樣,也可以根據(32,7,5,3,2,1,0)表示的32級LFSR的本原特征多項式得到32位隨機數。

3 正態分布隨機數的產生

正態分布隨機數可由(0,1)均勻分布隨機數產生,下面介紹兩種算法,一種基于中心極限定理,疊加均分分布隨機數產生;另一種基于公式變換,其產生的隨機數統計分布特性更好,但生成速度相對較慢。

3.1 統計近似抽樣法

統計近似抽樣[2]法的理論依據是著名的中心極限定理,它通過疊加均勻分布數據產生高斯噪聲,計算速度快,能夠滿足實時性要求。

當隨機變量相互獨立且服從同一分布時,中心極限定理可表述為：設隨機變量X1,X2,…,Xn,…相互獨立,服從同一分布,且數學期望和方差均存在且方差大于零,即E(Xk)=μ、D(Xk)=σ2≠0(k=1,2,3…),則隨機變量近似服從正態分布N(nμ,nσ2),即近似服從標準正態分布N(0,1)[3]。

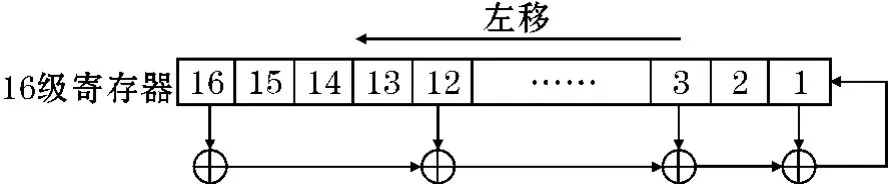
圖1 16級LFSR實現原理圖

服從(0,1)均勻分布的隨機序列X1,X2,…,Xn,…的數學期望和方差分別為則根據上述定理,服從N(0,1)正態分布。取合適的n值,就能產生N(0,1)正態分布的隨機數,試驗表明,n取6時就基本滿足要求,點數越大,高斯分布效果越好,實際實現方法要考慮硬件資源的限制,在效率和結果之間作出折中。

要得到兩路相互獨立、服從正態分布的高斯噪聲,可將上面方法得到的隨機數乘以正交的隨機相位即可。即若x是上述方法得到的一個隨機數,y是服從(0,1)均勻分布的隨機數,那么

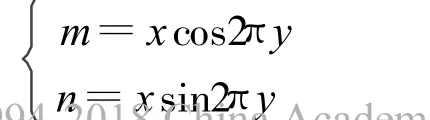
是相互獨立、服從正態分布的隨機變量,這樣就得到了兩路正交高斯噪聲。

3.2 變換抽樣法

變換抽樣法[2]基于Box-Muller變換[4],該方法可以產生分布特性非常好的高斯噪聲,但與統計近似抽樣法相比,其計算相對復雜,可用于低實時要求的系統中。

Box-Muller變換可表述為：設 x,y是兩個相互獨立的服從(0,1)均勻分布的隨機數,作如下變換：

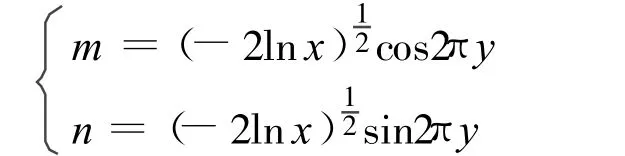
則可得到兩個相互獨立、服從N(0,1)正態分布的隨機數 m,n,即得到了兩路正交高斯噪聲。

4 高斯噪聲實時產生算法在ADSP-TS201S上的實現

4.1 ADSP-TS201S介紹

ADSP-TS201S是ADI公司一款性能極高、600MHz時鐘頻率、靜態超標量處理器[5]。處理器集成了24Mbits大容量存儲器,兼有ASIC和FPGA的信號處理性能,具有高度的可編程性與靈活性。處理器將非常寬的存儲器和雙運算模塊組合在一起,具有優異的并行處理能力,廣泛應用于無線通信、圖像處理等領域。

TS201S內部結構可分成內核和I/O接口兩部分,如圖2。這兩部分通過4條總線(J、K、I、S)傳送數據、地址和控制信號。內核部分包括程序控制器、數據地址產生器和XY雙運算模塊。程序控制器提供完全可中斷的編程模式,支持匯編語言、C/C++編程,支持10指令周期流水線,IAB可預存5條指令,BTB可減小分支跳轉延遲;數據地址產生器包含兩個ALU,支持立即尋址和間接尋址,支持位反序和環形緩沖尋址;雙運算模塊能夠獨立或同時工作以實現SIMD,每個周期每個運算模塊可執行2條運算指令。I/O接口包括內部存儲器、JTAG口、外部接口、DMA控制器和鏈路口。內部存儲器為大小是24Mbits的DRAM;JTAG接口可用于片上仿真;外部接口包括主機接口、SRAM接口、多處理器接口、EPROM接口;DMA通道共14個,可無需處理器干預下完成設備間的數據傳輸;雙向鏈路口采用低壓差分信號(LVDS)鏈路口技術,可達4Gbps的數據吞吐率[5]。

TS201S支持32位和40位浮點運算以及8、16、32、64位定點運算。每周期最多可執行 4條指令,在600MHz的時鐘頻率下,可達到每秒48億次乘加運算(GMACS)和每秒36億次浮點運算(GFLOPS)的速度[5]。

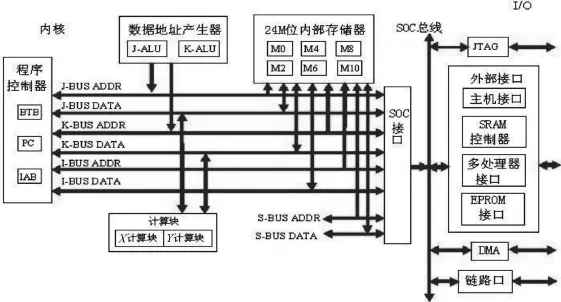
圖2 ADSP-TS201S內部結構框圖

4.2 算法實現

根據實時性要求,選擇線性同余法和統計近似抽樣法組合來產生實時高斯噪聲。線性同余法產生(0,65536)均勻分布的16位隨機整數,結果除以65536即得(0,1)均勻分布隨機數,此步驟合并到統計近似抽樣階段一次完成,以節約時間。試驗表明,統計近似抽樣法疊加點數n取6已基本達到要求。

為了進一步提高噪聲生成速度,此算法還采取了如下優化措施：

(1)正交隨機相位正余弦值通過查表獲得,事先建立了4096間隔[0,2π]正余弦表文件“cos-sin-4096.dat”,用到時直接隨機讀取;

(2)統計近似抽樣法6點均勻分布隨機數累加分兩組并行計算,節約處理器時間;

(3)利用ADSP-TS201S一指令行周期最多可以執行4條指令的特點[5],縮減程序長度,將可以并發執行的指令放在同一指令行,節約指令執行時間;

(4)利用ADSP-TS201S兩個運算塊可同時獨立進行計算的特點[5],減少循環次數,要得到正交兩路各2048點,共4096點的噪聲數據,只要循環1024次,每次生成兩對正交共4點噪聲。

具體程序代碼如下：

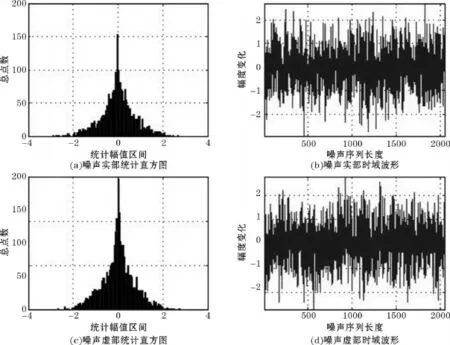
圖3 正交兩路高斯噪聲統計分布圖和時域波形圖

經試驗,程序在600MHz ADSP-TS201S上執行時間約100μ s,即能以10kHz的頻率連續產生兩路各2048點不重復的正交高斯噪聲。通過調試器dump出-noiseout[4096]的噪聲數據,用Matlab畫出的高斯噪聲的統計分布圖和時域波形如圖3所示,可見算法滿足實時性要求和分布特性要求。

5 結論

討論了幾種均勻分布隨機數和正態分布隨機數的快速生成算法,并在ADSP-TS201S上實現了其中一種算法,實時產生了滿足分布要求的高斯噪聲。該方法已成功應用到一款基于ADSP-TS201S的雷達模擬源中,并滿足參數要求。今后的工作可在程序優化部分作出改進,以進一步提高實時性。

[1]王衛江.實時高斯噪聲產生方法[J].Chinese Journal of Scientific Instrument,2006,27(11)：1523-1526.

[2]方崇智,蕭德云.過程識別[M].北京：清華大學出版社,1994：45-60.

[3]Marsaglia G.A Current View of Random Number Generator[J].Ann.Appl.Prob.,1991,(3)：461-481.

[4]李裕奇,何平.概率論與數理統計[M].北京：國防工業出版社,2004.

[5]劉書明,羅勇江.ADSP TS20XS系列DSP原理與應用設計[M].北京：電子工業出版社,2007.