自適應蟻群算法在YKK系列中型高壓電機優化設計中的應用
孟大偉,呂海鵬,徐 磊
(哈爾濱理工大學,哈爾濱 150040)
1 引言
電機的優化設計可以被描述為一個復雜的有約束、非線性、混合離散多目標規劃問題。在傳統優化算法出現計算困難的狀況下,應用現代啟發式算法能有效地解決此類問題,且其計算的可并行性,可以充分利用計算機的資源[1]。
相對于小型電機而言,中型高壓電機的優化設計存在著以下難點:
(1)變量的離散程度大 離散變量的存在使得大多數優化算法不能被直接使用。因此,要想將算法應用于電機設計當中,必須對算法進行適當的改進[2]。
(2)線規的選取 線規組合面積的變化規律異常復雜,而且可以選用的組合有限。因此,線規選取不當會對電機性能產生很大的影響。
(3)優化算法的選取 由于現在常用的優化算法,如模擬退火(SA)、遺傳算法(GA)、蟻群算法[3,4](ACA)的全局收斂性存在差異,所以,結合電機優化設計的特點選擇適合的算法顯得尤為重要。
本文重點介紹了ACA的基本思想及其特點,并結合電機優化的問題,詳細論述了蟻群算法在電機優化設計中的具體實現方法,最后將其應用到了YKK系列電機的優化設計,取得了較好的效果。
2 蟻群算法簡介
2.1 基本蟻群算法
現以求解典型的旅行商問題(Traveling Salesman Problem,TSP)為背景,說明蟻群系統模型。
TSP可以形象地描述為:假設平面上有n個城市,n個城市的TSP問題就是尋找通過n個城市各一次且回到出發點的所有路徑中最短的一條。
螞蟻從起始城市開始在相鄰城市之間轉移,直到達到目標狀態完成一次解的搜索。信息素強度是螞蟻進行城市間轉移的依據。每只螞蟻的轉移是根據轉移概率隨機進行的。從城市i轉移到某個相鄰城市 j的轉移概率為:
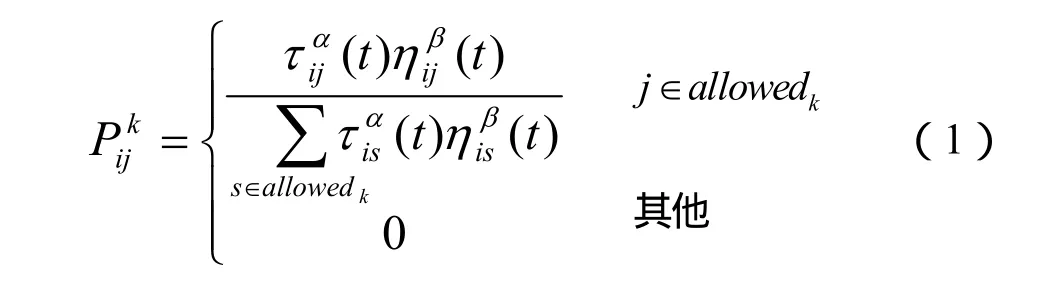
式中,τij(t)是t時刻搜索時城市i和j之間的信息素強度;α和β是大于零的參數;ηij是城市 i和j之間距離的倒數,是一種啟發信息;allowedk={1,2,…,n-1}表示螞蟻下一步允許選擇的城市。隨著時間的推移,以前留下的信息逐漸流逝,用參數1-ρ表示信息消逝程度,經過n個時刻,螞蟻完成一次循環,各路徑上信息量要根據下式進行調整:
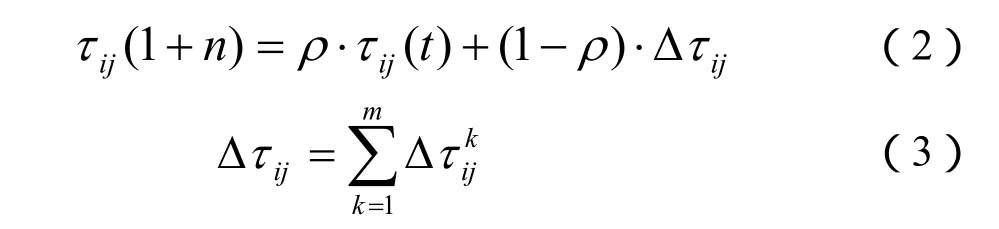

其中,Lk表示第 k只螞蟻在本次循環中所走過路徑的長度。
2.2 算法參數的選擇
幾乎所有的模擬進化算法的優化性能都與參數的選擇密切相關,不同的參數選擇對優化算法的影響很大。針對本文系列電機的優化,算法的參數選擇如表1所示。

表1 蟻群算法主要參數
3 系列電機串行優化設計的數學模型
一般,系列電機的優化設計多采用并行算法的思路,本文采用串行計算思路。串行優化設計也稱降維優化設計,即將復雜多規格共沖片電機設計問題轉化為單規格電機優化設計問題。其單規格電機優化數學模型可描述為以下問題的極值:
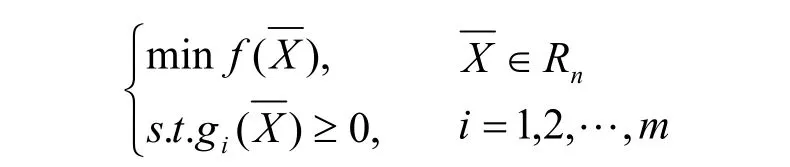
3.1 優化設計的目標函數
由于目標函數的建立是影響著優化設計向何處去的關鍵且本課題的主旨是“節能”,因此本文選擇效率為目標函數。可表示為
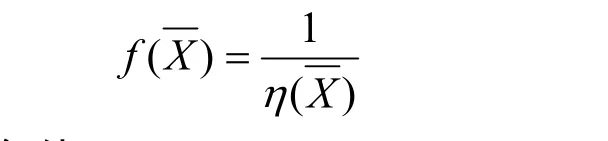
3.2 約束條件
約束條件可分為兩類,一類為基本約束條件;另一類為一般約束條件。
基本約束條件為電機性能要求,即效率、功率因數、起動轉矩、最大轉矩、 起動電流以及熱負荷,具體可表示為
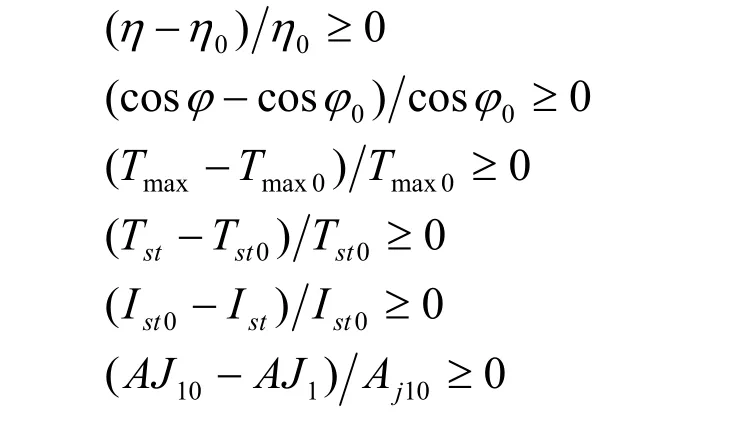
下標帶“0”者為相應標準值。
一般性約束條件包括優化變量的非負約束,且多為強制性約束,如本文中的幾何尺寸約束:
(1)對線規的約束
本文所用線規的寬邊和窄邊尺寸均在企業所規定的扁線限用表內選取。
(2)定子槽型尺寸與線規應滿足的約束
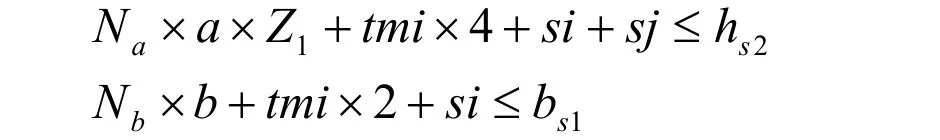
其中:Na為導體縱向并排個數;a為導體絕緣后高度;si為松散量;Z1為槽內導體數;tmi為主絕緣厚度;sj為層間墊條厚度;hs2為定子槽有效高度;Nb為導體橫向并排個數;b為導體絕緣后寬度;bs1為定子槽寬度。
(3)對槽楔的約束
當定子槽楔的寬b≥14mm時,槽楔厚度為5mm,否則為4mm;槽楔的相對磁導率為4μ0。
3.3 優化變量
系列電機設計中最重要的特點之一就是若干規格的電機采用相同的定、轉子沖片。因此,共沖片電機設計須將設計變量分為兩類:一類是公用變量'X,包括各規格電機相同的變量,例如本文選擇的定子槽寬bs1,定子槽高hs2,轉子槽寬br1、轉子槽高hr2;另一類是非共用變量''X,包括各規格電機可以各自獨立變化的變量,本文選擇的鐵心長度L、槽內導體數Z1、線規尺寸均為非共用變量。
3.4 串行優化法的實現
串行優化法首先需要人為地從多規格中選出一個重點規格。本文選擇功率最大的電機為重點規格,以其效率最高為目標,按全部設計變量進行優化設計。得出該規格的優化方案后,則固定“公用變量”值,而針對“非公用變量”對其他各規格電機逐一優化。如有不夠理想的方案,可以適當調整后再重復上述計算,直到全部規格滿足要求為止。
4 蟻群算法的改進及其在電機優化設計中的應用
4.1 改進的自適應蟻群算法
電機優化設計問題規模比較大,由于信息量的揮發系數ρ存在,使那些從未被搜索到的信息量會減小到接近于0,降低了算法的全局搜索能力。根據公式(1)和(2),解的信息量隨著ρ的增大而增大,以前搜索過的解被再次選擇的幾率就大,收斂速度也就越快,從而降低了到算法的全局搜索能力。然而,減小ρ雖然可以提高算法的全局搜索能力,但又會使算法的收斂速度降低。因此可以自適應地改變ρ的值。ρ(t0)=1;當算法求得的最優值在N次循環內沒有明顯改進時,ρ減為
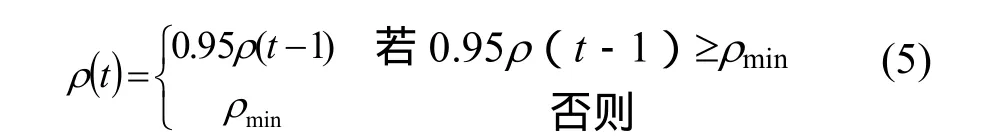
其中ρmin為最小值,可以防止ρ過小降低算法的收斂速度。本文N和ρmin分別選為50和3。
4.2 蟻群算法在電機優化設計中的應用
對于電機優化設計,選擇一個合適的算法固然重要,但更重要的是結合電機設計的特點對算法進行適應性的改進并應用到設計當中。本文算例涉及的中型高壓系列電機優化設計具備如下特點[5]:
(1)電機屬于系列化產品,出于管理與經濟上的原因,對極數相同、容量相近的電機采用共沖片設計。因此,這類優化設計中的優化變量有共用與非共用之分;
(2)電機參數的非連續性要求其變量搜索必須按離散方式進行,以使優化空間的任一探測點都能滿足工程實際的需求;
(3)優化目標函數與約束函數的相悖性,常使得電機優化設計的最優點位于邊界上;
(4)電機設計數值函數是非線性程度很高的復雜問題,必須協調好全局尋優與收斂速度之間的矛盾。
結合上述特點,電機優化程序流程如下:
(1)構建路徑
首先,將設計變量轉化為優化變量,并構成蟻群算法中螞蟻的可行域。可行域以矩陣的形式存在,如圖1所示。
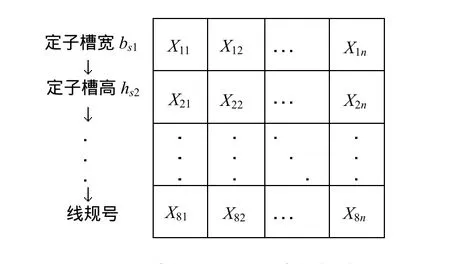
圖1 優化變量所組成的矩陣
(2)對約束條件進行處理
目標函數f(x),服從于gi(x)≥0,i=1,2,…m,其中m是約束的數量。然后,可將等價的非約束優化問題描述為
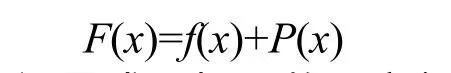
將懲罰函數設置成目標函數,它懲罰任何對于約束的違背,強迫非約束優化朝著可行的區域進行。懲罰函數P(x)定義如下

式中Ri是懲罰參數,被認為是懲罰因子。按約束違背的水平,相應地變化Ri。
(3)構建信息素矩陣
信息素τij表示當螞蟻從第i行變量選擇第j行變量的期望度。它也以矩陣的形式存放,與變量矩陣相對應,如圖2所示。
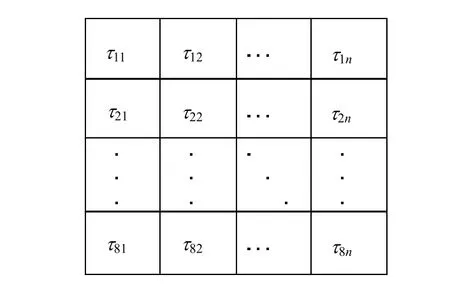
圖2 信息素矩陣
(4)啟發式信息
α的大小表明每個路徑上信息量的受重視程度,α值過大會使搜索過早陷于局部最小點。β的大小表明啟發式信息的受重視程度。本文對α和β得選擇參照表1。
(5)解的構建
螞蟻根據公式(1)計算出的概率從其可行鄰域(即所有螞蟻k還沒有訪問過的變量)中選擇下一個變量,逐步完成對每個優化變量的選擇。將選擇出的優化變量通過接口轉化為設計變量送入主程序完成電磁核算并進行方案評估。
(6)信息素更新
根據公式(2)、(3)、(5)更新信息素矩陣。
(7)檢驗是否符合結束條件,如果當前的迭代次數達到了預先設定的最大次數,則停止迭代,輸出最優解,否則轉到(2)。
5 算例及分析
應用如表1所選參數的自適應蟻群算法對YKK系列高壓三相異步電動機進行優化。計算符合以下條件:
(1)不變動統一設計的系列型譜以及對相同極數和同一機座號共用定、轉子沖片的原則;
(2)統一設計中的定轉子內、外徑尺寸和軸尺寸以及定、轉子槽的形狀不允許改變,不能任意更動槽配合;
(3)鐵心材料為w400硅鋼片;
(4)槽楔磁導率μ=4μ0;
(5)風摩耗值仍以統一設計值為依據。
表2和表3列出了YKK500-2共沖片三個規格電機(2000kW、2240kW、2500kW)結果對比情況。
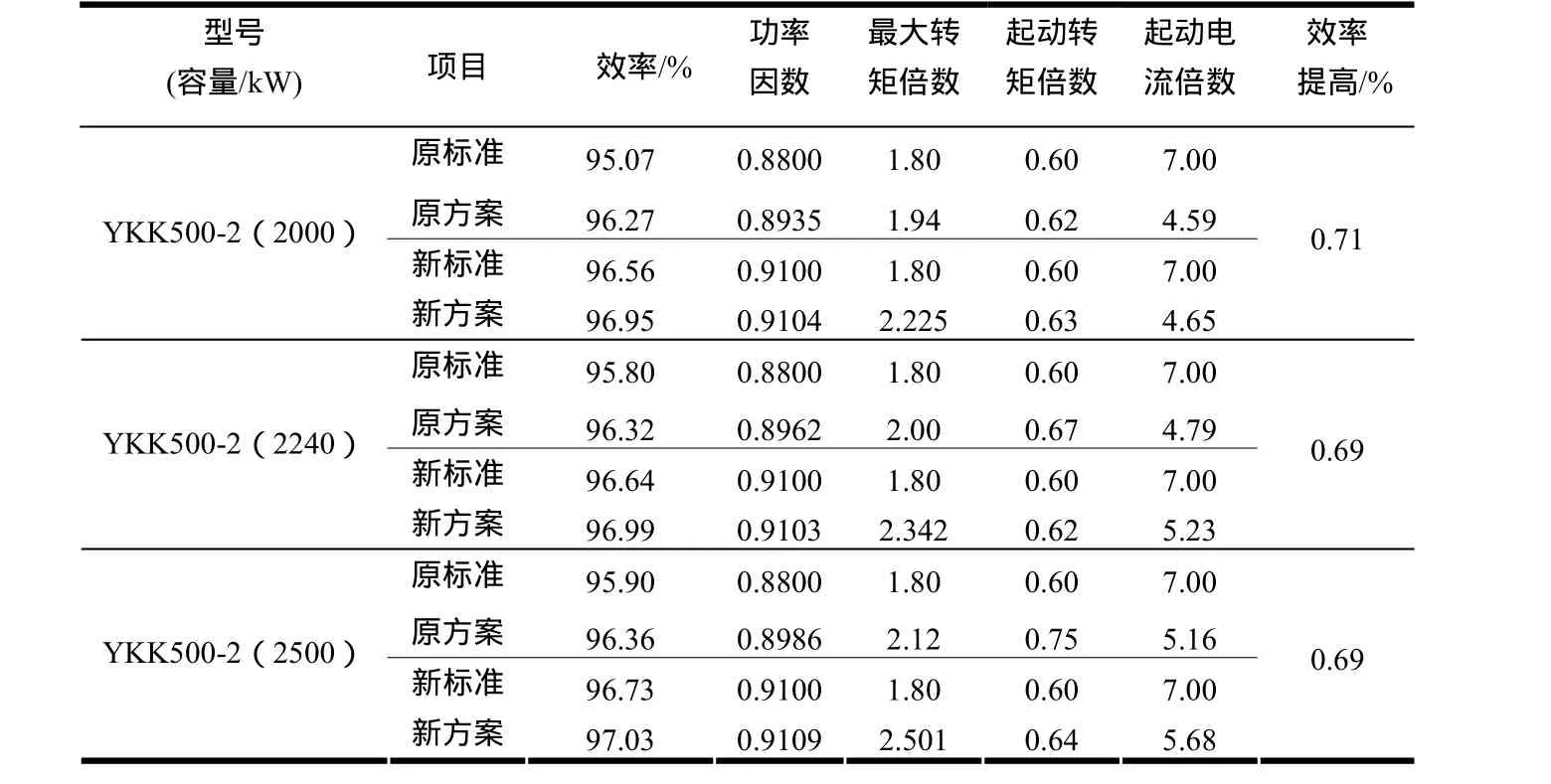
表2 性能指標對比

表3 有效材料用量
5.1 性能指標分析
分析表2的性能指標表明:原方案的效率和功率因數均不能滿足新設計標準,而采用自適應蟻群算法優化過的新方案則完全滿足標準,效率分別提高了0.71%、0.69%、0.69%,均有一定的設計裕度。最大轉矩倍數的平均值為2.356,比原方案的最大轉矩倍數平均提高16.63%。
5.2 經濟指標分析
表3所示三種規格電機,中心高由原來的560降為新設計方案中的500,D1/Di1由原來的990/560變為現在的900/500,體積有了明顯的縮小,線規尺寸較原方案也有了很大的縮小,有效材料用量有了很大程度的節省。
新設計方案定子繞組用銅平均節約14.86%,硅鋼片用量平均節約18.14%。
6 結論
本文結合電機設計的特點及工程實際對蟻群算法做了改進。經過實例計算表明,效率、功率因數和最大轉矩有所提高,優化結果令人滿意。因此,算法具有工程實際意義。
[1]張善兒,陳世元.現代電機優化設計啟發式算法[J].微特電機,2006,1(2):94.
[2]孟朔,趙爭鳴.異步電機的優化設計新方法[J].清華大學學報(自然科學報).2001,41(6):120-123.
[3]M Dorigo,L M Gambardella.Ant Colony System:A Cooperative Learning Approach to the Traveling Salesman Problem[J].IEEE Trans.On Evolutionary Computation,1997,1(1):53-66.
[4]M Dorigo,G Di Caro.The Ant Colony Meta-heuristic.In:D Corne.M Dorige,F Golver( Eds.) New Ideas in Optimization,McGraw-Hill[M]. New York,1999.11-32.
[5]孟大偉,周美蘭.模擬退火算法在電機設計中的應用[J].電機與控制學報, 2001, 5(3).

