感應電機最大效率控制規律研究

曾令宏，覃煥昌

(1.柳州師范高等專科學校 物理與信息科學系, 廣西 柳州 545004;2. 百色學院 物理與電信工程系，廣西 百色533000)

1 引言

感應電機由于具有可靠性高、價格低的優點，在工業領域獲得了大量的應用，但是它在輕載情況下效率低的缺點限制了它的應用[1]。

為研究感應電機驅動最大效率控制，需要建立相應的控制系統損耗模型。以往文獻建立的感應電機數學模型很少從系統損耗與效率的角度出發，而只是考慮電機的動靜態性能[2]。由于電機工作在大范圍變化的轉速和轉矩下，以往的控制策略只是保證電機在額定工作點附近保持較高的效率，而對于負載變化較寬的感應電機驅動系統考慮較少。另一方面，很多效率優化是建立在將鐵耗等效電阻視為常數基礎上的，這種假設也會對效率分析產生很大的誤差。

感應電機可以看成是一個兩輸入兩輸出系統，輸入量可歸結為定子電壓及其頻率，而輸出量為轉子轉速和轉矩[3]。簡單地說，在變頻驅動中，在輸出轉矩和轉速一定的情況下，即輸出功率不變時，施加在電機定子繞組上的電壓和頻率可以有不同的組合，其中存在某一最佳的電壓和頻率組合使電機在該點輸入功率最小，即損耗最小、效率最大。本文主要建立感應電動機的損耗模型，給出了各個損耗的計算表達式；詳細研究鐵心損耗及其變化規律；利用感應電機損耗模型進行仿真研究，得出采用最大效率控制時以不同變量為控制量的控制規律。

2 感應電機驅動系統損耗模型

感應電機損耗主要包括定子銅損耗、定子鐵損耗、轉子銅損耗、轉子鐵損耗、附加損耗和機械損耗。機械損耗和雜散損耗在總損耗中所占比例小，一般各占5%和10%左右。而且這兩種損耗取決于電機參數，幾乎不可控[4]。

銅損耗和鐵損耗是決定電動機效率的主要因素，鐵損耗與頻率有關，間接與勵磁電流有關而與負載電流無關；而且勵磁電流也會產生定子銅耗，負載電流將決定轉子銅耗，轉子銅耗與轉差密切相關[5-7]，所以驅動系統效率大小是隨負載狀況而變化的。輕載時，勵磁電流較大，如果適當降低電壓則鐵損會降低，效率會增加，但是如果電壓降低過低，則在輸出功率不變的情況下，電流增加得厲害，損耗反而增大；換句話說，保持在一定的轉矩和轉速，可使電機在大磁通小轉差或小磁通、大轉差情況下運行。

為了分析方便，給出感應電機一相穩態等值電路，如圖1所示。

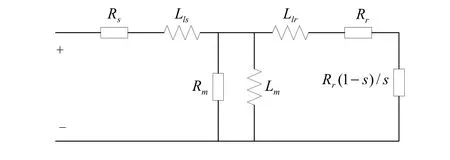
圖1 感應電機一相穩態等值電路

銅耗分為定子銅耗和轉子銅耗兩部分，可由式（1）、（2）表示。定子銅耗：

轉子銅耗：

式中：s——轉差率；

——電磁功率。

因此在電磁功率不變時轉子銅耗與轉差率成正比。

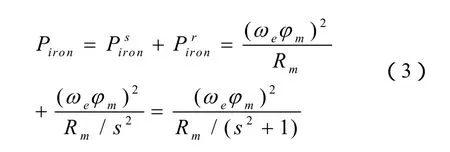
式中：eω——定子電流角頻率；

rω——轉子轉速；

——轉差頻率。

電機的機械損耗可由以下公式給出：

式中，KL為機械損耗系數。可見機械損耗主要與電機轉子速度有關。

附加雜散損耗為：

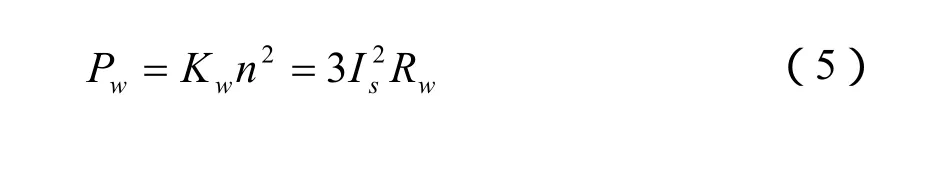
附加雜散損耗主要是由定轉子齒槽效應、導體的集膚效應等引起的附加損耗。它主要與負載轉矩、定子電壓、頻率和溫度等量相關[68]。

綜上所述，電機輸入功率Pin為：

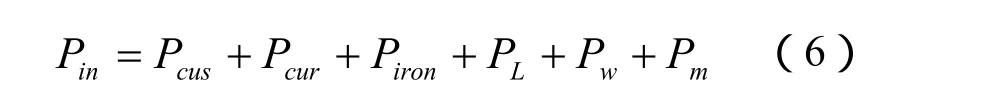
式中，Pm為輸出的機械功率，它的計算公式為：

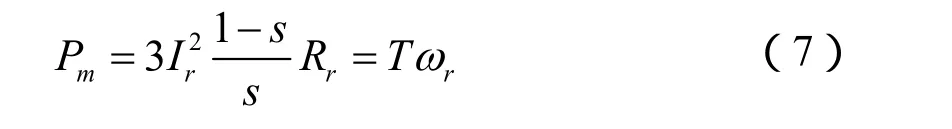
而輸入功率Pin在這里根據等值電路圖有：

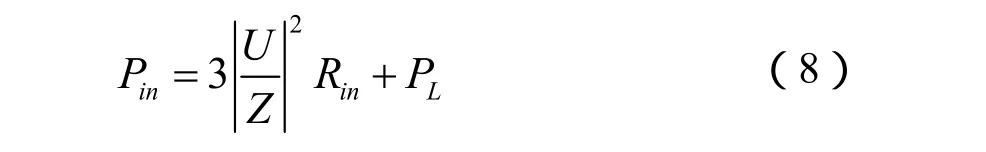
式中：U——定子一相輸入電壓；

Z——定子一相輸入阻抗；

——定子一相輸入阻抗的實部。

3 最大效率點的解算依據

最大效率控制一般以Pin為目標函數，對于自變量，可以選擇轉差、磁通、定子電壓等變量，本文以轉差s作為自變量來說明最大效率解算的依據。

首先需要明確Pin與s的函數關系，為解算最大效率點，有：

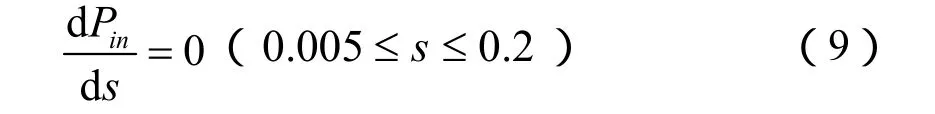
圖2為某感應電機在負載轉矩T=30N?m，轉速n=1000r/min時一相輸入功率相對于轉差率的關系。圖3為負載T=40N?m，轉速n從200r/min增加到1400r/min時輸入功率與轉差的關系圖。

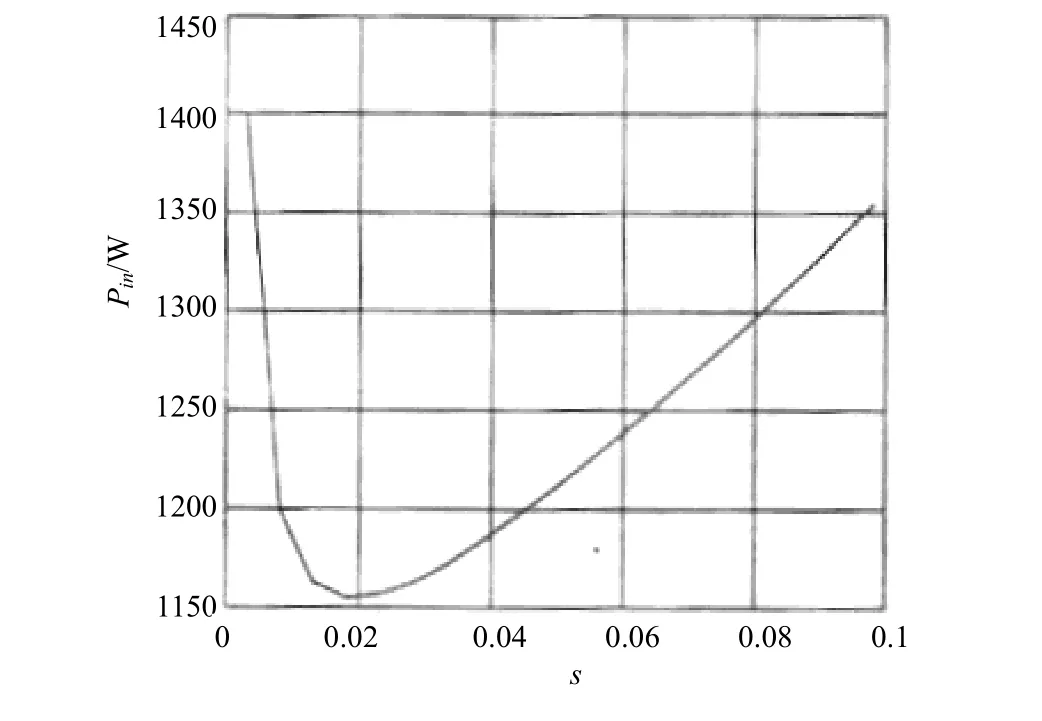
圖2 T=30N?m，n=1000r/min輸入功率與轉差的關系圖

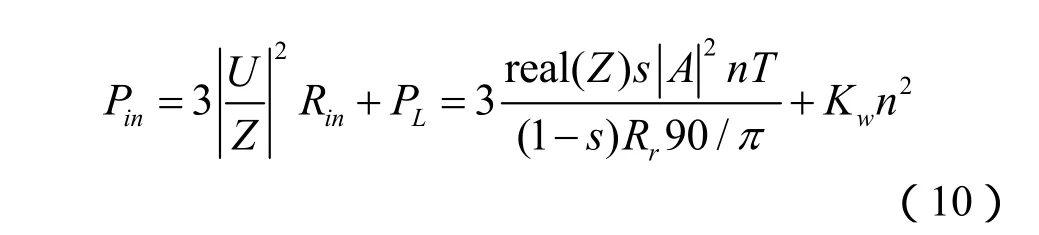
其中：

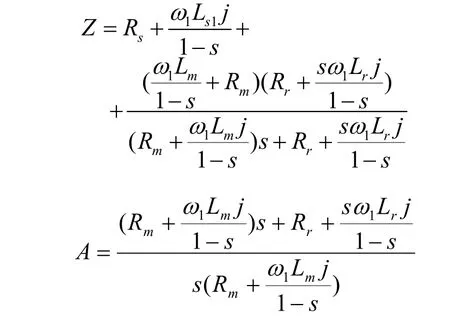
式中：real為取實部的意思，j為虛數單位。

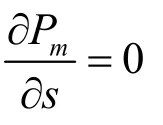
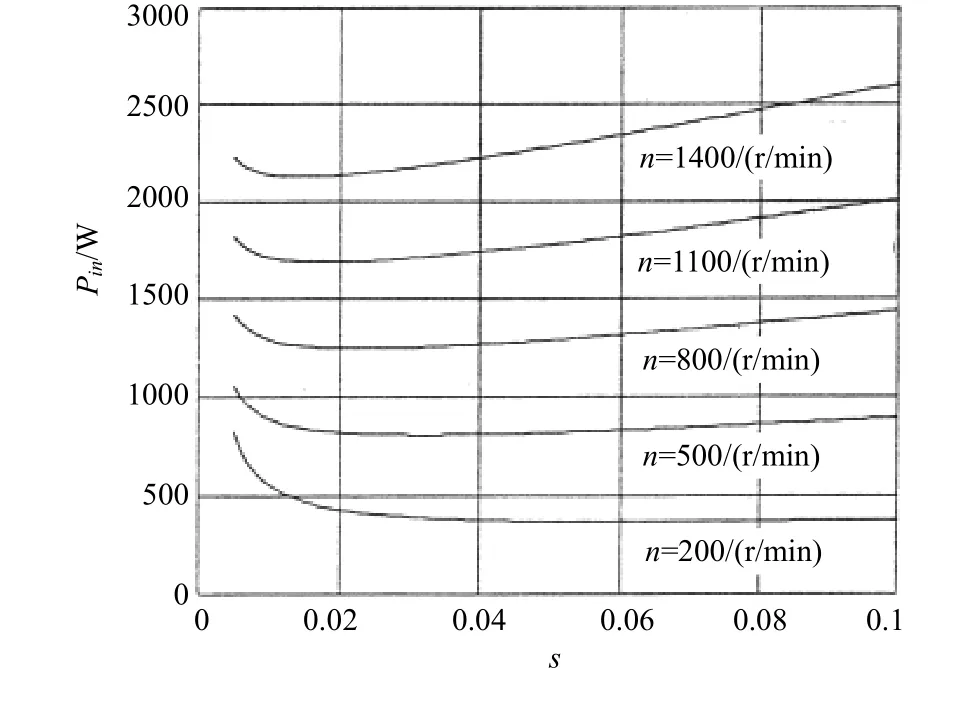
圖3 T=40N?m，n從200r/min到1400r/min的輸入功率與轉差圖

4 最大效率控制仿真研究

最大效率控制仿真是以轉速和轉矩為輸入來求解滿足系統效率最大時對應的輸出，即表征電機的輸入量。這里將選取轉差作為輸入量，對最大效率控制仿真。

仿真的基本工作流程為：讀取電機參數，在給定的T和n的條件下，根據公式（10），調用求極值模塊求解Pin的最小值，并得出對應的轉差。為便于比較分析，選取傳統的恒磁通控制，即頻壓比控制作為比較。

仿真電機參數如下：

表1 感應電機參數

圖4和圖5分別為最大效率控制時的效率圖和傳統恒頻壓比控制時的效率圖。將這兩個圖對比，不難看出，最大效率控制下的效率曲面明顯抬高，特別是在負載較輕或速度較小的情況下效率提高更大。效率增加量見圖6。參見圖4、圖5和圖6，可知如果速度不變，則轉矩在左右時效率增益最小，效率絕對增加量最大為24.48%，效率絕對增加量平均為4.79%。最大效率 91%發生在 T = 4 8N? m， n = 1 300r/min，最小效率66.1%發生在 T = 7 2N? m， n = 1 50r/min ，平均效率86.63%。在T接近額定轉矩且轉速在/2以下和 T ≤/4時，最大效率控制都能使效率增加5%以上，當 T =/2時效率增加較小，約為 1%；而在額定點及其附近區域增加僅為 0.11%。表 2為兩種控制方式下的效率相對增加數據。綜上所述，以大約/2為輕載和重載的分界線，采用最大效率控制后，負載越輕效率增加越明顯，尤其在輕載條件下，效率增加更大；另一方面，速度越低則效率增加越明顯。

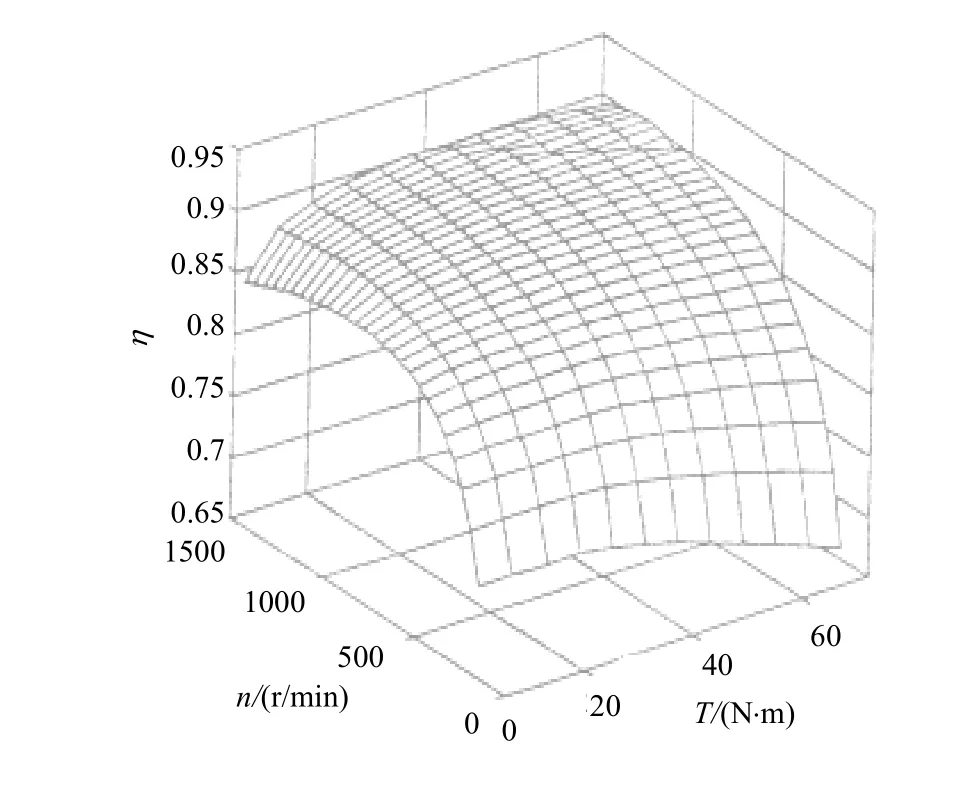
圖4 最大效率控制時的效率圖

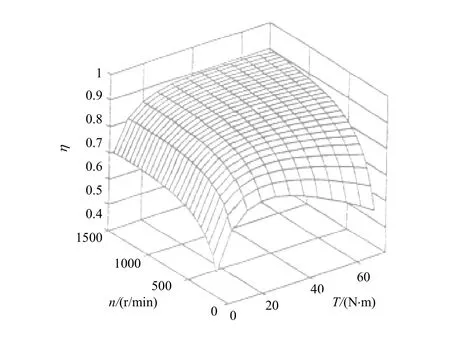
圖5 頻壓比控制下的效率圖

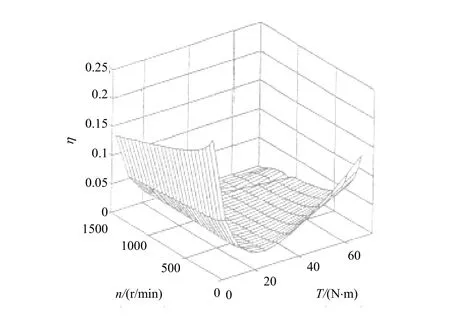
圖6 效率增加圖

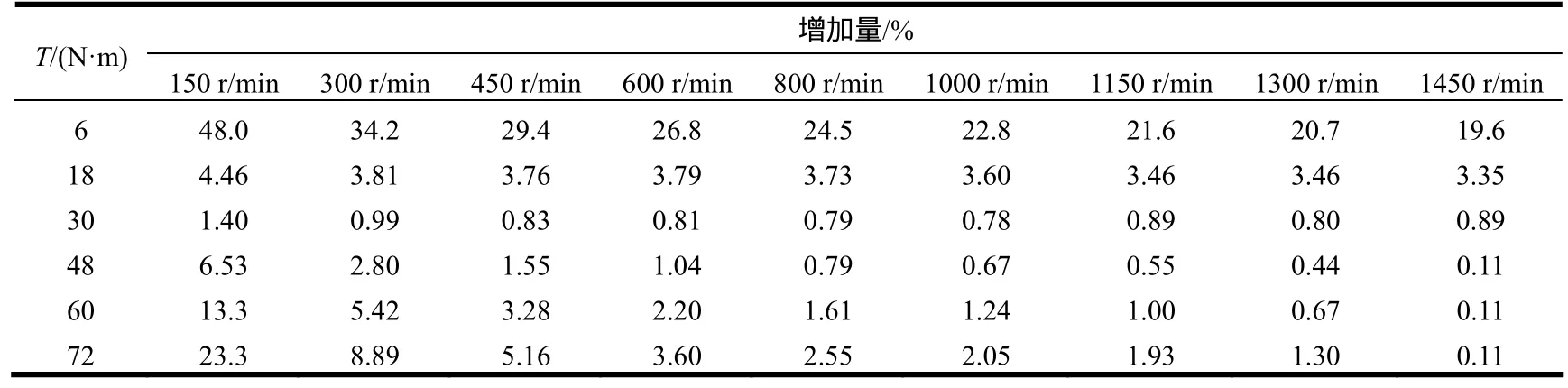
表2 最大效率控制下的效率相對增加量

5 結論

本文從電驅動系統的基本特性出發，給出了靜止坐標系下感應電機一相等效電路。同時給出了最大效率點解算的依據，即在一定的負載轉矩和轉速下，輸出功率保持不變的情況下，控制某個變量使電機輸入功率最小，那么該點的最大效率控制點也就找到了。并以轉差為控制變量，對最大效率控制規律進行了仿真研究。仿真結果可以說明，最大效率控制與傳統頻壓比控制相比，效率曲面明顯抬高，效率提高的區域明顯增大了。并且低速輕載情況下效率增加更為明顯。

[1]李永東. 交流電機數字控制系統[M]. 北京: 機械工業出版社, 2002.

[2]Green,T.C.,Hernandez-Aramburo, etc. Losses in grid and inverter supplied induction machine drives[J]. IEE Proceedings: Electric Power Applications, 2003, 150(6):712-724.

[3]周志剛. 一種感應電機的解耦控制方法[J]. 中國電機工程學報, 2003, 23(2): 121-125.

[4]莫紅蘋，鐘彥儒. 基于銅耗等于鐵耗的異步電動機最佳效率控制[J].西安理工大學學報, 2002,18(2): 167-170.

[5]Bottauscio, Oriano, Chiampi,etc. Additional losses in induction machines under synchronous no-load conditions[J]. IEEE Transactions on Magnetics,2004, 40(5):3254-3261.

[6]Mi, Chunting Chunting Chris. Minimization of iron losses of permanent magnet synchronous machines[J]. IEEE Transactions on Energy Conversion, 2005, 20(1):121-127.

[7]Rao, K.S. Rama, Ramamoorty, M. Design optimization of inverter fed 3-phase squirrel cage indu-ction motor[J].IEEE Region 10 Annual International Conference, Proceedings/TENCON,2003, 4(8):1303-1307.