基于自適應Backstepping方法的艦船電力系統混沌控制

蔡亮 周濤

(江蘇海事職業技術學院電氣工程系，南京 212000)

1 引言

艦船電力系統是一個非線性、強耦合、多變量的高階復雜系統，而非線性系統在一定參數條件下會進入混沌狀態。對于電力系統來說，混沌現象的發生，會表現為一種非周期性的，似乎是無規則的、突發性或陣發性的機電振蕩。現有研究表明混沌運動有可能作為電力系統擾動失穩過程的一個中間階段而存在[1-2]。在艦船的航行中，電機員多次在電力系統運行中觀測記錄到了這種振蕩，這對艦船電網的安全運行構成了潛在的威脅，可能導致系統失穩[3-4]。因此，對艦船電力系統進行混沌研究有非常大的實際意義。

目前，電力系統的混沌研究主要針對于陸上電力系統，而艦船電力系統較陸上電力系統有容量小，線路短，工作環境濕度大等特點[5]。不同于陸上電力系統，有關艦船電力系統混沌研究仍處于起步階段，以理論分析和仿真研究為主。在有關艦船電力系統混沌現象的研究中，文獻[3]、[4]深入研究了艦船電力系統的雙機并聯運行的工況，經過變換得到了一個適合分析艦船電力系統混沌運動的模型。文獻[5]研究艦船電力系統運動狀態隨參數改變的過程，文獻[6]中利用Melnikov和Lyapunov指數這兩種方法作為判據，對兩機并聯艦船電力系統的混沌現象進行數值分析，結合系統的功率譜分析，提高了分析系統發生混沌振蕩的準確性，指出當發電機之間存在功率傳遞和受到一定幅值的周期性負載擾動時，艦船電力系統將出現混沌振蕩。對于混沌現象的控制，理論研究中已有大量的控制方法，并不一定能夠直接應用于工程實際中的混沌系統。本文在文獻[4]給出的雙機并聯運行艦船電力系統混沌運動的模型以及文獻[6]對混沌現象的數值分析基礎之上，采用Backstepping自適應控制方法，能夠將混沌系統中的任意的不穩定點控制到該混沌系統的平衡點上。通過數字仿真，表明了該控制方法的有效性。

2 艦船電力系統混沌模型

[4]所提供的兩臺發電機并聯運行時，形成的發電機互聯系統。其基本供電網絡結構可等效表示成圖 1。其中， E1∠ δ1和E2∠δ2分別為系統中的兩臺發電機電動勢，和分別代表兩臺發電機的同步電抗， xl和 rl為分別是線路電阻和電抗，由于艦船電力系統中線路短，故線路電阻非常小，常忽略不計，P，Q表示系統負荷。

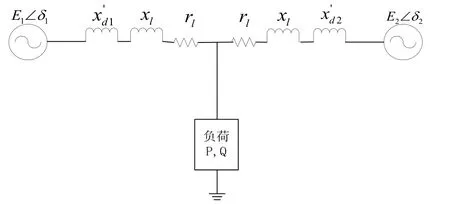
圖1 兩機并聯模型

考慮發電機參數相同的情形，并記δ=δ1-δ2,ω=ω1-ω2為兩臺等值發電機的相對功角和相對功角速度。則兩機互聯系統具有以下形式：

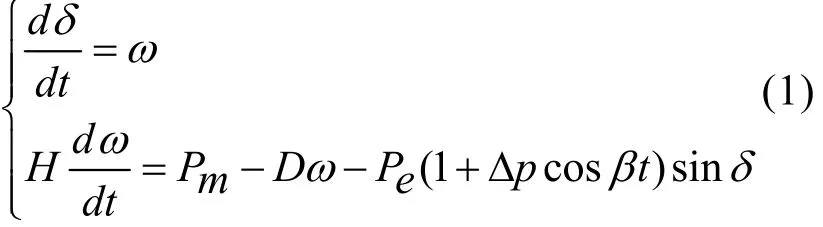
式中，H、D為等值轉動慣量和等值阻尼系數；Pm為發電機輸入機械功率， Pe為系統輸出的電磁功率。 Δ p? pec os βt 是為了研究船艦電力系統在擾動下混沌運動而引入的電磁擾動，其中Δ p? pe表示擾動的幅值，β表示擾動的頻率。

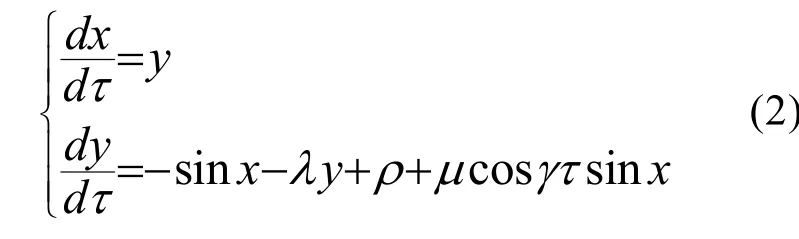
3 采用自適應Backstepping艦船電力系統混沌的控制

這里所說的自適應Backstepping方法是指利用Backstepping方法設計一個自適應控制器，當系統已經處于混沌運動，該控制器能夠將任意的不穩定點控制到該混沌系統的平衡點上，能夠達到迅速抑制混沌的目的。這里針對艦船電力系統的混沌運動來設計控制器，根據自適應Backstepping的設計方法[7],引入一個控制輸入u加入到狀態方程(2)中，如式(3)所示：

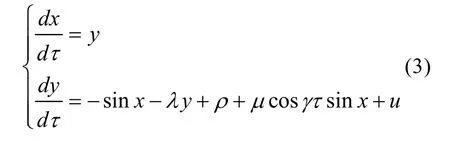
由(3)式中的第一個方程，為了使V1( x)= x2/2的導函數負定，特為y設計穩定化函數α1(x)。假設α1(x)= - k1x( k1＞0)并定義以下誤差變量

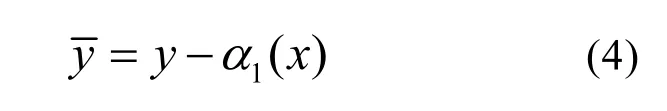
為了設計簡單，不妨設 k1= 1 ，則于是有關于的方程組

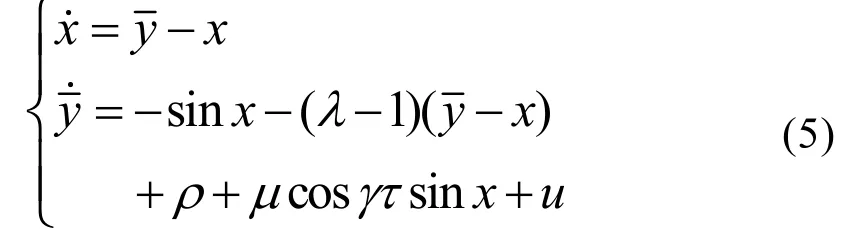
定義Lyapunov函數

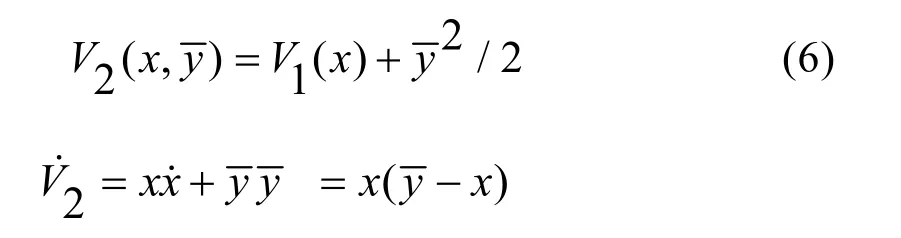
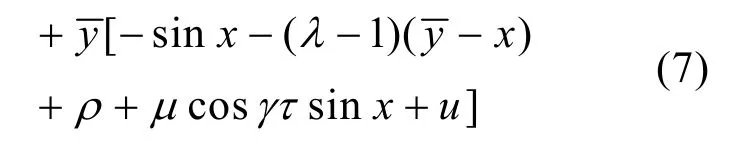
若

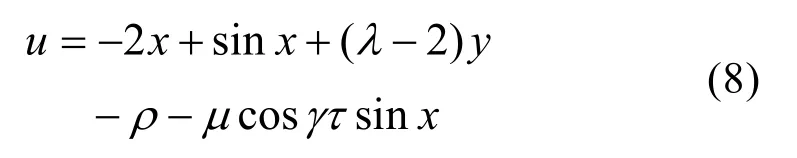
若擾動幅值μ為未知參數，利用μ?作為μ的參數估計，向其逼近，控制器應為：

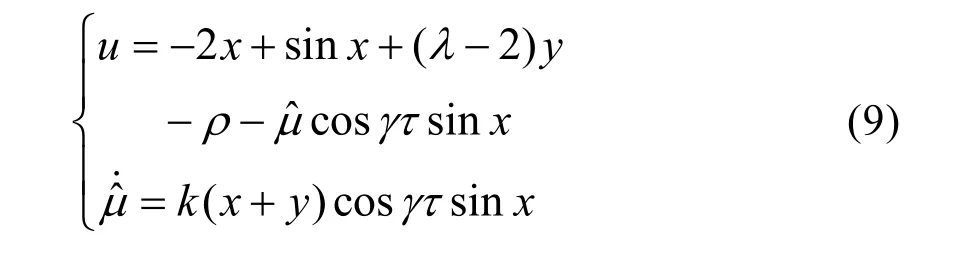
式中 k ＞ 0 ，可以調節自適應律的速度。

加入控制器，則艦船電力系統的狀態方程為

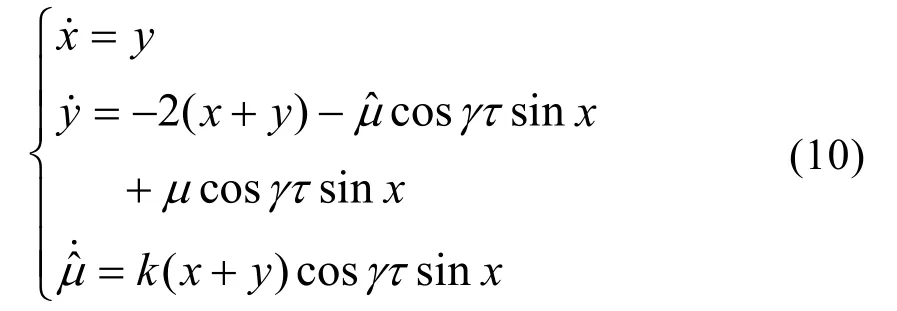
變換得

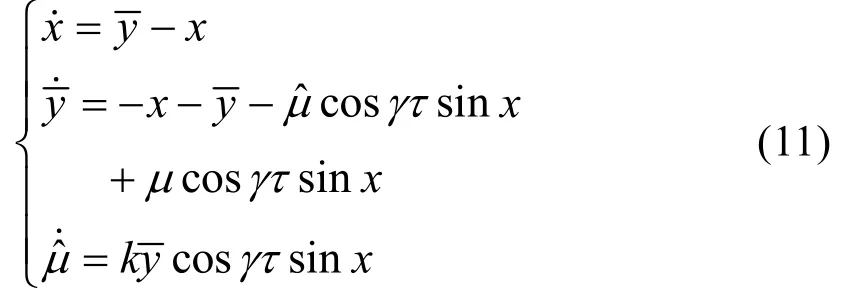
為證明在控制器(9)的作用下，系統是漸進穩定的，取Lyapunov函數：

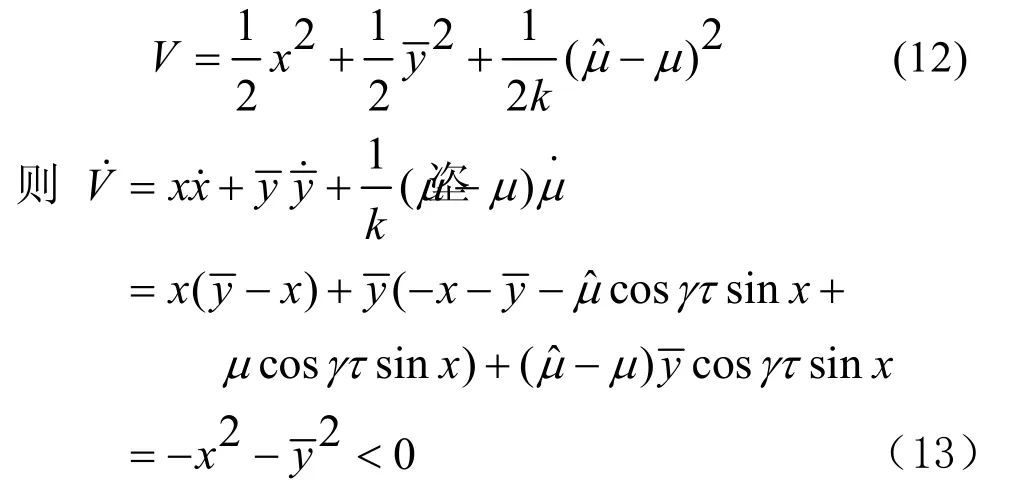
4 數字仿真

由艦船電力系統混沌運動的數值分析，得到在參數λ=0.4，ρ=0.2，擾動頻率γ=0.8的情況下，當擾動幅值μ=1.3時，系統處于混沌狀態[6]。為了抑制混沌，引入控制器(9)，在系統處于混沌狀態運行100s后，投入控制器，受控系統的動態相應及相圖如圖2、圖3、圖4、圖5所示。

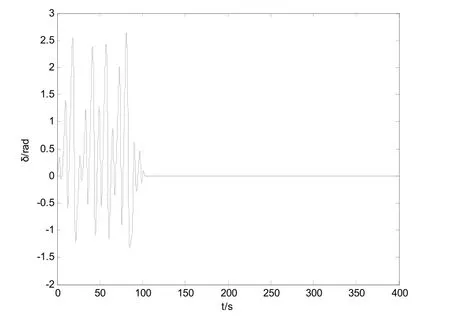
圖2 功角δ的變化曲線 擾動幅值μ =1.3

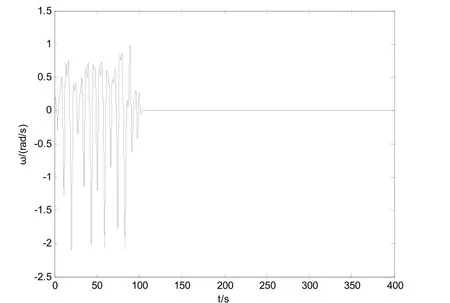
圖3 功角速度ω的變化曲線擾 動幅值μ=1.3

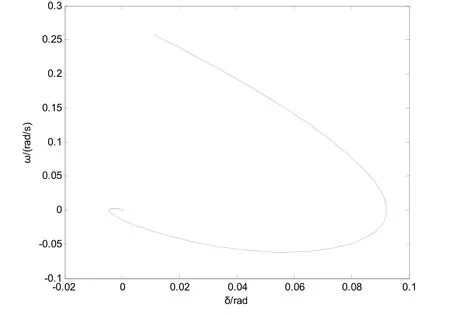
圖4 功角δ和功角速度ω相圖擾動幅值μ=1.3

從圖2功角δ的變化曲線和圖3功角速度ω的變化曲線可以看出，在控制器作用下，艦船電力系統的混沌運動得到了迅速的抑制，且回到了平衡點。圖4功角δ和功角速度ω相圖也顯示了這一點。圖5μ?-1.3的變化曲線反映了受控系統能夠很好辨識系統的幅值，但是存在一定的誤差，從仿真的過程來看，其誤差的大小與k的選取有關。不過，實驗的目的在于能夠抑制艦船電力系統的混沌運動，從仿真的效果來看，無疑達到了目的，說明了自適應Backstepping方法在控制系統混沌的有效性。

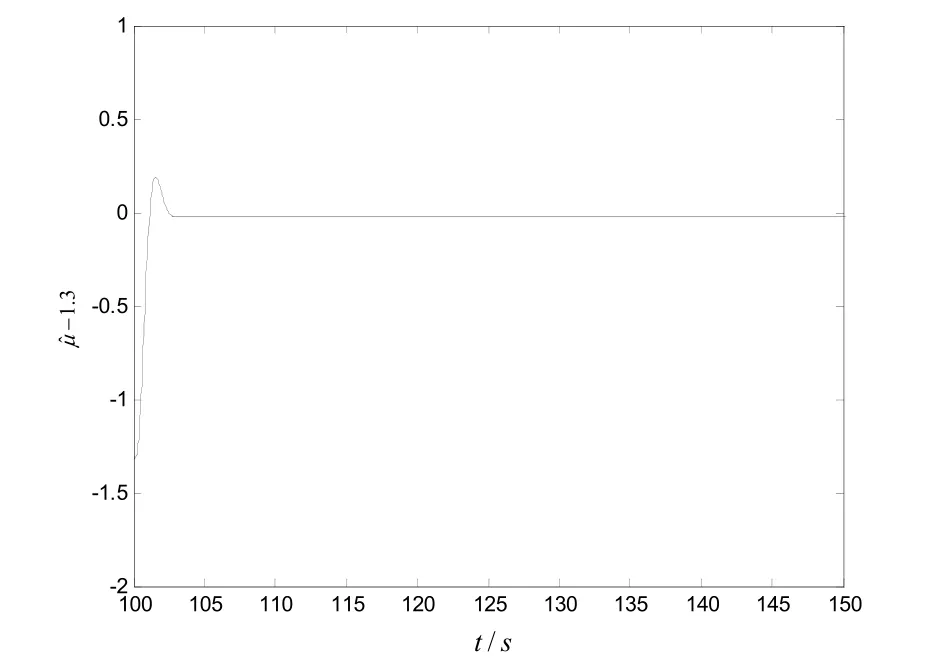
圖5 μ?-1.3的變化曲線

5 結束語

本文運用自適應Backstepping方法分別對艦船電力系統的混沌運動進行了控制。實現了系統已經處于混沌運動，投入控制器，使系統穩定到混沌系統的平衡點，同時還保證該系統的全局穩定性。能夠達到迅速抑制混沌的目的。

參考文獻：

[1]張強. 電力系統非線性振蕩研究[J]. 電力自動化設備. 2002, 22(5)： 17-19.

[2]賈宏杰，余貽鑫，王成山. 電力系統混沌現象及相關研究[J]. 中國電機工程學報, 2001, 21(7)： 26-30.

[3]施偉鋒. 關于艦船電力系統研究的一些探索[D]上海：上海海事大學, 2005.

[4]黃健. 船舶電力系統混沌現象研究[D]. 上海：上海海事大學, 2005.

[5]劉金波. 艦船電力系統暫態穩定性分析[D]. 哈爾濱：哈爾濱工程大學, 2002.

[6]蔡立勇. 艦船電力系統混沌運動的數值分析[J]. 船舶工程.2008, 30(3)： 53-56.

[7]武玉強，李洪亮，孫海龍. 基于 Backstepping方法的多變量系統自適應控制[J]. 控制與決策, 2001：93-96.