基于八叉樹編碼的點云數據精簡方法

邵正偉， 席 平

（北京航空航天大學機械工程及自動化學院，北京 100191）

在逆向工程中，非接觸式測量方法獲取的被測物的數據一般具有無序、海量的特點[1]。無序的特點是指每個數據點只具有三維坐標值的信息，而沒有明確的空間鄰域信息，不利于鄰域數據點的搜索，而鄰域數據點的搜索速度正是影響散亂數據處理和曲面重構效率的主要因素之一。海量的特點是指測量數據過密，這不但會影響曲面的重構速度，而且在重構曲面的曲率較小處還會影響曲面的光順性。因此，在進行曲面重構前，需要建立數據的空間鄰域關系和精簡數據。文中應用八叉樹編碼的空間鄰域劃分方法，并在此基礎上提出了一種新的點云數據均勻精簡方法。

1 點云精簡方法

近年來，人們做了很多關于數據精簡方面的研究，主要包括曲率精簡和均勻精簡兩類方法。在曲率精簡方法中，洪軍[2]先利用包圍盒法構造分割面，然后利用分割面將點云處理成掃描線結構，再利用角度、弦高聯合準則法逐線精簡；周綠[3]使用了拋物面擬合法求解局部曲率，再根據曲率偏差對點云進行精簡。在均勻精簡方法中，萬軍[4]通過以某一點定義采樣立方體，求立方體內其余點到該點的距離，再根據平均距離和用戶指定保留點的百分比進行精簡，該方法由于沒有預先對點云數據劃分空間鄰域，在檢索采樣立方體過程中，需要對全部點云數據進行判斷，因此處理海量數據時計算量較大，且不能根據指定的點距精簡點云。

針對以上方法的不足，文中提出新的均勻精簡方法的原理是：

（1）根據指定的點距，應用八叉樹編碼法對點云進行空間鄰域劃分，把點云數據的空間包圍盒（最小外接立方體）劃分為多個指定點距d0邊長的子立方體，具體方法見2節；

（2）分別對每個子立方體進行數據精簡，如圖1所示，若在劃分后的某兩個相鄰子立方體中存在8個數據點p1～p8，保留每個子立方體中距中心點最近的點p3和p7。由于相鄰子立方體中心點的距離為d0，所以精簡后點云中p3和p7之間的距離也近似為d0。

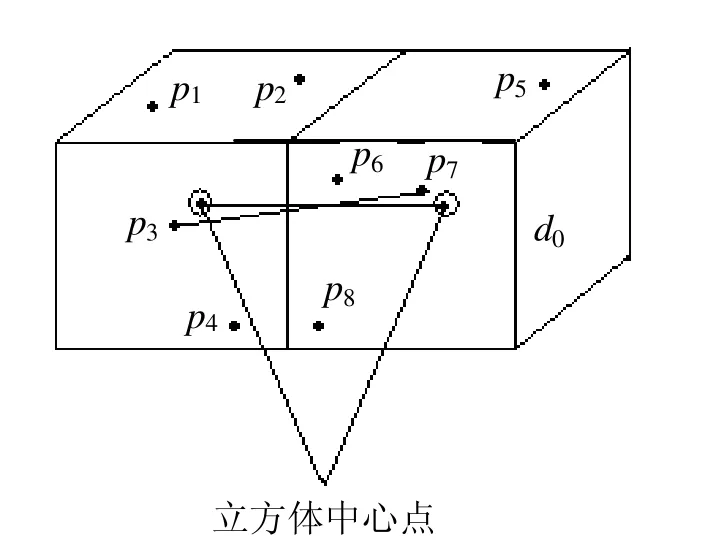
圖1 點云子立方體

2 空間鄰域劃分

在對散亂數據進行精簡、濾波、特征提取等處理過程中，需要獲取數據點在其型面對應點處的單位法矢、微切平面及曲率值等信息，這就需要搜索數據點的k近鄰，即在數據點集中尋找k個與該點歐氏距離最近的點。一般的搜索方法就是窮舉法：計算某點與點集中其余點的歐氏距離，并按從小到大排序，選取排在前面的K個點為該點的k個最近鄰點。對于海量點數據，這種搜索方法耗時極大，因此，為點云建立良好的空間鄰域結構是提高數據點 k近鄰搜索速度的關鍵。

下面介紹一種在逆向工程中常采用的空間鄰域劃分方法——八叉樹法。

2.1 八叉樹法原理

八叉樹結構是區域四叉樹向三維空間的推廣，是通過遞歸分割點云空間的方式實現的。首先構造點云數據的空間包圍盒（外接立方體），并把它作為數據點云拓撲關系的根模型；再將外接立方體分割成大小相同的8個子立方體，每個子立方體均視為根節點的字節點；如此遞歸分割，直至最小子立方體的邊長等于給定的點距，將點云空間hu劃分為2的冪次方個子立方體。

在八叉樹劃分過程中，子立方體的編碼與其所在的位置有關[5]。如圖2所示，規定：在x軸上位于x中分面右側的子節點編碼均比左側相鄰節點編碼加1；在y軸上位于y中分面前側的均比后側的相鄰節點位置碼增加2；在z軸上位于z中分面上側的均比下側的相鄰節點位置碼增加4。

圖2 八叉樹空間劃分模型

對于一個正立方體包圍盒空間進行遞歸八等分，假設剖分層數為n，則八叉樹空間模型可以用n層八叉樹表示，八叉樹空間模型中的每個立方體與八叉樹中的結點一一對應，它在八叉樹空間模型中的位置可由對應結點的八叉樹編碼Q表示

其中 qm為八進制數表示該節點在其兄弟節點之間的序號，而qm+1表示qm節點的父節點在其同胞兄弟節點間的序號。這樣，從q0到qn-1完整地表示出八叉樹中的每個葉子節點到樹根的路徑。

2.2 點云數據編碼

點云數據編碼的步驟為：

（1）確定點云八叉樹剖分層數n，滿足

其中 d0為精簡的指定點距，dmax為點云包圍盒的最大邊長。

（2）確定點云數據點所在子立方體的編碼，假設數據點 P ( x , y,z )，所在子立方體的空間索引值為(i, j,k )，Q為與子立方體相對應的結點的八叉樹編碼。三者的關系可由公式(3)～(5)表示[6-8]

其中 (xmin,ymin,zmin)表示與根節點對應的包圍盒的最小頂點坐標值，[…]為取整操作符。

將索引值(i , j,k )轉換為2進制表示方式

則子立方體對應的八叉樹編碼可由公式(1)表示。同時，如果已知子立方體對應的八叉樹編碼Q，也可以反求出數據點所在子立方體的空間索引值(i , j,k )

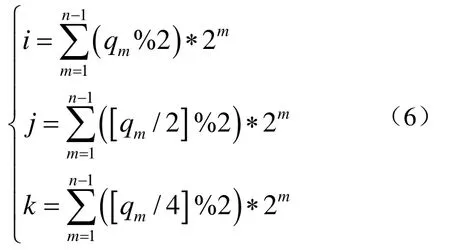
其中 (qm%2)表示對qm除以 2所得余數，[qm/2]表示對qm除以2所得結果取整數。

在搜索數據點的k近鄰時，可在數據點所在的子立方體及其周圍相鄰的 26個子立方體中搜索。若空間某子立方體的索引值為(i , j,k )，則其周圍 26個子立方體的索引值可由(i ±δ, j ±δ,k±δ)表示，δ ∈ {0 , 1}。因此，經過八叉樹劃分后的點云，只需要在局部進行k近鄰搜索，明顯提高了搜索速度。

3 應用實例

基于八叉樹編碼的均勻精簡算法的流程如圖3所示，在UG軟件平臺上使用C++語言二次開發了點云數據的預處理模塊，如圖4所示。并針對渦輪葉片模具的測量數據進行精簡，圖5所示為初始測量點云，包含數據點24500個，圖6所示為指定精簡距離為 2mm的精簡后點云，包含數據點 4607個，精簡后的點云在空間分布均勻，適合數據的后續處理。

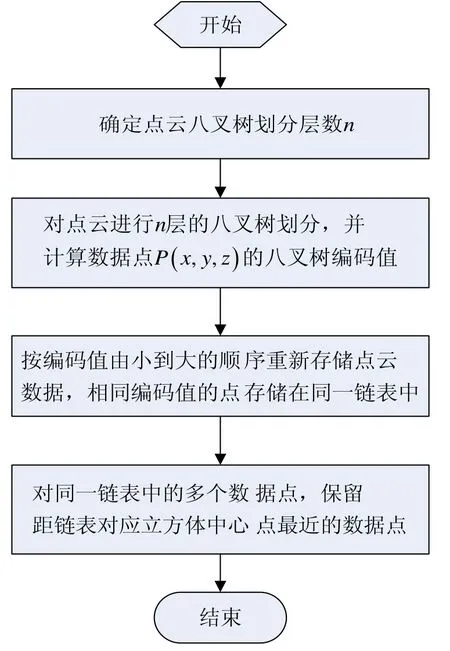
圖3 算法流程圖

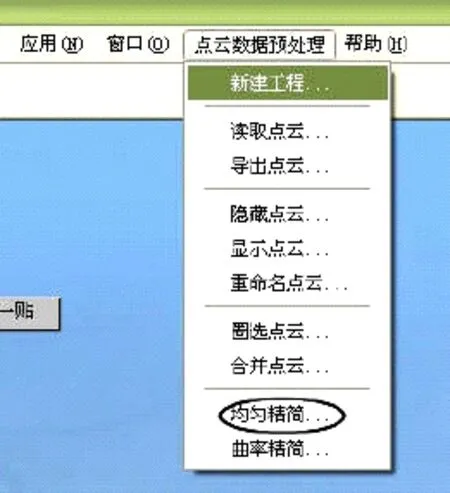
圖4 點云數據的預處理模塊

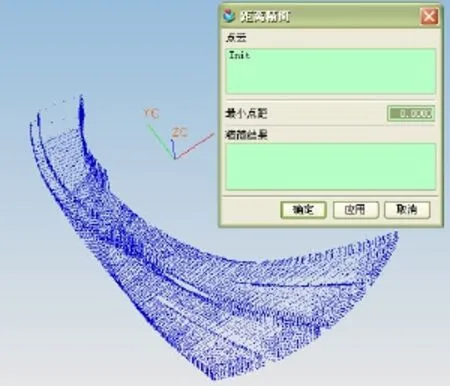
圖5 初始測量點云

圖6 精簡后點云

4 結 論

本文提出的點云精簡算法能對逆向工程測量的海量數據做出快速有效的精簡，算法具有以下特點：

（1）從空間整體角度考慮點云的均勻精簡，精簡效果較好；

（2）由于精簡前對點云進行了空間劃分，因此算法簡潔、高效；

（3）用戶通過設定精簡點距，可以靈活實現點云精簡。

[1]孫肖霞, 孫殿柱, 李延瑞, 等. 反求工程中測量數據的精簡算法[J]. 機械設計與制造, 2006, (8): 37-38.

[2]洪 軍, 丁玉成, 曹 亮, 等. 逆向工程中的測量數據精簡技術研究[J]. 西安交通大學學報, 2004, 38(7):661-664.

[3]周 綠, 林 亨, 鐘躍先, 等. 曲面重構中測量點云精簡方法的研究[J]. 中國制造業信息化, 2004, 33(5):102-104.

[4]萬 軍, 鞠魯粵. 逆向工程中數據點云精簡方法研究[J]. 上海大學學報, 2004, 10(1): 26-29.

[5]張傳明, 潘 懋, 徐繪宏. 基于分塊混合八叉樹編碼的海量體視化研究[J]. 計算機工程, 2007, 33(14):33-35.

[6]范 茵, 汪德宗. 八叉樹編碼的三維物體截面之比計算[J]. 數據采集與處理, 1999, 14(1): 47-51.

[7]趙 強. 基于BSP樹的點云精簡方法研究[D]. 西安:西北工業大學, 2007.

[8]孫肖霞. 基于UGII的反求工程數據處理技術研究與系統開發[D]. 淄博: 山東理工大學, 2006.