推力磁軸承的優化設計與有限元分析
楊芳芳,呂建超
(中國燃氣渦輪研究院,四川 成都 610500)


1 引言
電磁軸承作為一種新穎的非接觸式支承部件,因具有無接觸、無潤滑、無磨損、少維修、壽命長、可靠性高等特點和良好的轉子動力學特性而得到學術界和企業界廣泛的關注。目前,航空航天工業已成為國際上電磁軸承應用的主要領域之一,電磁軸承可大大提高航空技術的現代化水平。主動推力磁軸承是電磁軸承系統中的一種,由于其具有轉子位置、軸承剛度和阻尼可由控制系統確定等優點,在磁懸浮應用領域中得到了廣泛的應用[1]。
在工程實際中,經常遇到在已知定子內、外徑的條件下設計主動推力磁軸承。本文在已知定子內、外徑的條件下,根據承載力和溫升的要求設計了一套推力磁軸承,并利用有限元分析軟件對推力磁軸承的電磁特性進行了驗證。
2 推力磁軸承優化設計
推力磁軸承的結構示意圖如圖1所示。
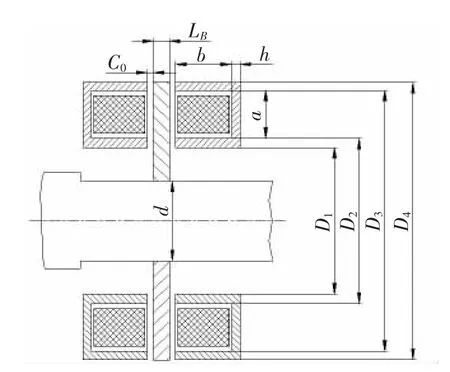
圖1 推力磁軸承示意圖Fig.1 Scheme of thrust electromagnetic bearings
推力磁軸承最大名義懸浮力Fmax為[2,3]:
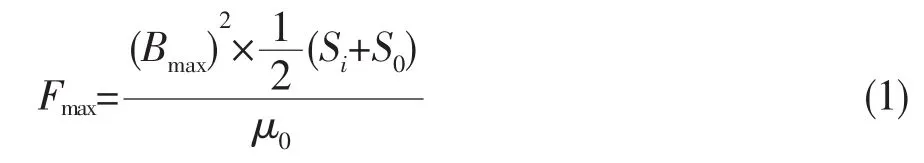
現取相等的內、外環面積,則:

由此可知:
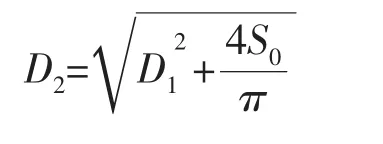

如果磁軛高度h太小,可考慮取最小磁軛工藝尺寸,一般h≥3 mm。并令推力盤寬度LB=1.5h。
線槽深度b未知,考慮磁路方程定子部分的影響,令

可得:

實際設計時要考慮實際線徑(標稱線徑)的規格,并重新計算j的值。下面分別在給定的承載力(最大)、允許的溫升及工作氣隙的磁感應強度約束條件下,以體積最小為目標函數進行優化。
(1)承載力:Fmax≥W。由于計算內、外磁環面積時已考慮,故在目標函數中不另行考慮。
(2)實際溫升:
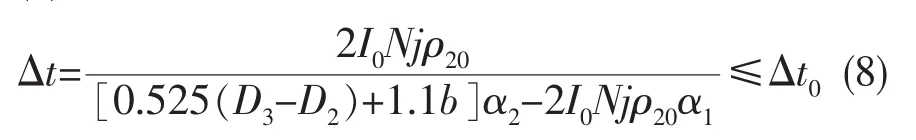
整個定子中鐵芯的體積:

定子中含銅的體積:

設最小體積為目標函數f(X),考慮參數約束條件,數學模型可表示為:

針對上述優化數學模型可采用復合形法、罰函數法、序貫加權因子(SWIFT)法等優化算法優化得到最優推力磁軸承結構。
3 優化算列
在一工程實例中,已知定子外徑D4為119 mm,定子內徑D1為65.5 mm,軸向承載力W為1 800 N,安全系數ns為1.1,定子的材料為1J22,其最大磁感應強度Bmax為2.2 T,工作氣隙c0為0.5 mm,偏置電流 I0為2.5 A,最大電流密度 jmax為4.5 A/mm2,填充系數 Kc為 0.9,允許溫升 Δt0為 150℃,銅線 20℃時的電阻率 ρ20為 0.018 Ω·mm2/m,電阻溫度系數 α1為0.004 261℃-1,給定散熱條件下的散熱系數α2為20 W/(m2·℃)。
優化得到的結構參數見表1,優化設計的推力磁軸承的結構見圖2。
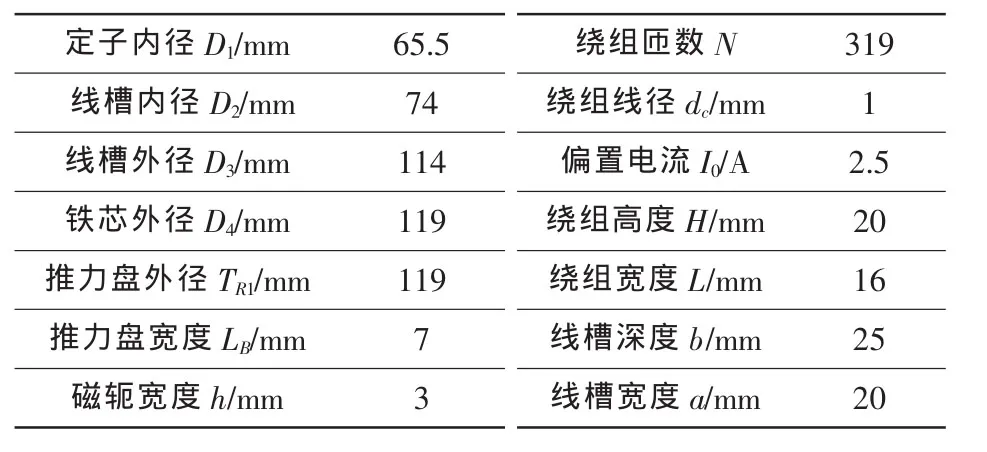
表1 優化參數Table 1 Optimized parameters

圖2 推力磁懸浮軸承結構Fig.2 The structure of thrust magnetic bearings
4 推力磁軸承有限元分析
電磁軸承電磁力的計算方法有磁路方法和場域方法兩種。場域方法作為一種更精確的分析方法,以數值計算為基礎,可以更加細致地考察諸如磁場分布、邊緣效應、極間耦合、渦流、軸承結構等因素的影響。常見的數值法有有限元法和邊界元法。
電磁場內在規律由電磁場Maxwell基本方程組來表述,電磁軸承中的磁場分布同樣服從Maxwell方程組[4]。Maxwell方程組是分析和計算電磁場問題的出發點。有限元法計算的未知量(也稱自由度)主要是磁位或電位,其它諸如磁場磁通密度、電流密度、能量、力、損耗、電感和電容可以由這些自由度導出。
推力磁軸承分析屬于靜態場分析,此時Maxwell方程變為[5]:

同時,當轉子處于平衡位置時,推力磁軸承的磁場屬于典型的軸對稱形式[6],所以可以采用二維靜態磁場分析。
轉子處于平衡位置時,對推力磁懸浮軸承作電磁特性分析,此時磁極上施加的工作電流為偏置電流I0。材料不同的各個面積賦予不同的材料特性,其中定子和推力盤的材料為1J22,空氣和導線區域材料的相對磁導率μΓ為1。在導線區域施加電流密度載荷,整個結構的最外層節點施加磁力線平行邊界條件。
推力磁軸承一側的有限元模型如圖3所示,其磁力線分布見圖4。由圖中可以看出,空氣媒質中的磁力線與分界面近于垂直,而且漏磁現象不嚴重。

圖3 推力磁軸承有限元模型Fig.3 The finite element model of thrust magnetic bearing

圖4 磁力線分布圖Fig.4 Flux distribution
從圖5所示的磁感應強度分布圖可以看出,最大磁感應強度在外磁環氣隙處。圖6所示為氣隙中磁感應強度分布圖。圖中橫坐標DIST代表鐵芯與推力盤之間的氣隙位置。由圖6可以看出,內磁環氣隙中的磁感應強度達到0.93 T,外磁環氣隙中的磁感應強度達到1 T,氣隙中的磁感應強度略小于0.5Bmax,此時電磁力為776 N。

圖5 磁感應強度分布圖Fig.5 The distribution of flux density
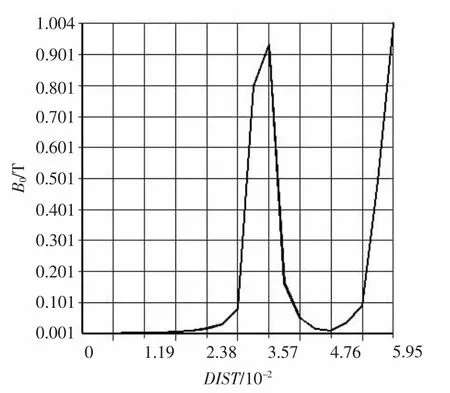
圖6 氣隙中的磁感應強度分布圖Fig.6 Flux density in the air
5 結論
針對工程需要,以承載力最大和溫升滿足要求為目標優化設計出一套推力磁軸承,并用ANSYS軟件對其電磁力進行驗算。結果表明,在轉子處于平衡位置時,利用有限元計算的推力磁軸承鐵芯與推力盤之間的磁感應強度與理論值0.5Bmax僅差0.1 T,此計算結果與文獻[6]的結論相符。由此可以推斷出,優化設計出的推力磁軸承滿足承載力最大的要求。
[1]施韋策G,布魯勒H,特拉克斯勒A.主動磁軸承基礎、性能及應用[M].虞 烈,袁祟軍,譯.北京:新時代出版社,1997.
[2]Imlach J,M S,Allaire P E.Magnetic Bearing Design Optimization[J].Imech,1998,C277/88,53—60.
[3]Hsiao F Z,Chung C F.Optimum Magnetic Bearing Design Considering Performance Limitations[J].JSME International Journal,1996,39(3):586—596.
[4]胡業發,周祖德,江征風.磁力軸承的基礎理論與應用[M].北京:機械工業出版社,2006.
[5]閻照文.ANSYS工程電磁分析技術及實例詳解[M].北京:中國水利水電出版社,2006.
[6]劉淑琴,徐 華.推力電磁軸承的電磁場分析[J].磨擦學學報,2000,20(1),42—45.

