基于PCA-SVMR快速測定復方氯丙那林和對乙酰氨基酚

郭嘉偉，謝洪平

（1.第三軍醫(yī)大學藥學院，重慶 400038；2.蘇州大學藥學院，江蘇 蘇州 215123）

1 引 言

近紅外光譜（NIRS）分析方法是一種便捷、快速、無污染的分析測試技術(shù)，通過多元校正模型可實現(xiàn)多組分快速同時測定[1-2]。其關(guān)鍵技術(shù)環(huán)節(jié)之一是建立量測數(shù)據(jù)的校正模型，而常用的方法有多元線性回歸、逐步回歸、主成分回歸和偏最小二乘（PLS）等[3]。這些方法均是建立在大量分布均勻的已知樣本基礎(chǔ)之上的傳統(tǒng)的統(tǒng)計學習方法，然而，在實際的分析工作中往往難以獲取大量的已知樣本，同時，近紅外數(shù)據(jù)與組分濃度間常呈現(xiàn)非線性映射關(guān)系，因此近紅外光譜小樣本體系的非線性建模方法將成為人們關(guān)注的問題[4-5]。建立在統(tǒng)計學理論基礎(chǔ)上的支持向量機（Support Vector Machine，i.e.SVM）算法[6-7]可以有效地解決小樣本體系的非線性建模的準確度問題，該類問題在藥物復方制劑以及生產(chǎn)過程的快速測定中更為突出。《中國藥典》對復方氯丙那林和復方對乙酰氨基酚兩種制劑均難于實現(xiàn)多組分快速同時測定[8]，該文將以主成分分析（PCA）為基礎(chǔ)，結(jié)合SVM回歸（SVMR）即PCA－SVMR方法對該兩類制劑在小樣本情況下的快速測定方法進行研究，并對PCA-SVMR法在藥物復方制劑中的應(yīng)用進行方法學考察。

2 SVMR基本原理[9-11]和PCA-SVMR方法

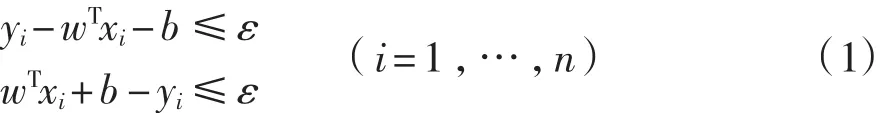
統(tǒng)計學理論將通過使結(jié)構(gòu)風險最小化來逼近實際風險，即控制函數(shù)集的復雜度使回歸函數(shù)最平坦，等價于最小化若允許存在擬合誤差（即引入松弛因子與，即式（1）為：

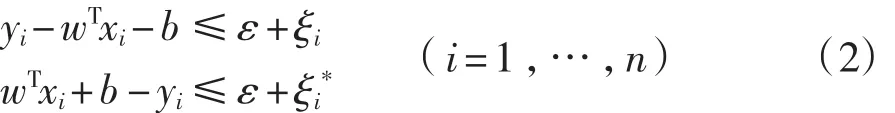
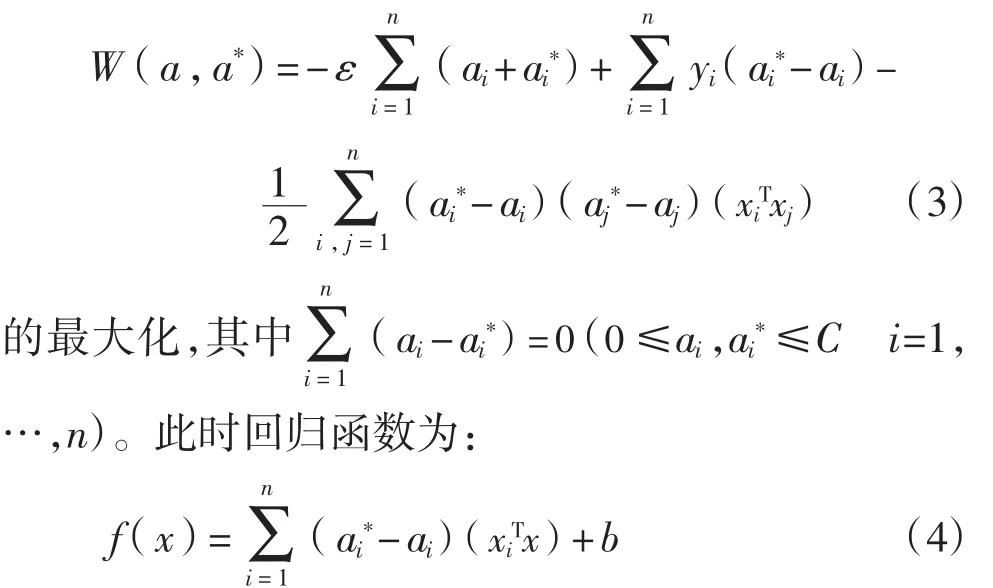
對于非線性映射，可以用泛函理論中滿足Mercer條件的一種核函數(shù)K（xi·xj）將低維空間的非線性問題轉(zhuǎn)換為高維空間中的線性問題，即式（3）和式（4）中在低維空間中的內(nèi)積（xiT·xj）將用高維空間中的內(nèi)積運算K（xi·xj）代替。其中SVM使用的核函數(shù)主要有多項式、徑向基和Sigmoid等3種形式。

由于NIRS的量測信號較弱，干擾信號相對增強，特別是復方藥物制劑中存在的多種有效組分和輔料將對被測組分構(gòu)成嚴重的信號干擾，使多元校正模型的預測能力降低，在小樣本體系中該類現(xiàn)象將更為突出。為了解決此問題，該文將以PCA方法提取其有用量測信息，再以SVMR方法建立其多元校正模型（即PCA-SVMR法）。

3 實 驗

3.1 儀器與試藥

傅里葉變換NEXU紅外光譜儀（美國Thermo Electron公司），配有積分球漫反射采樣系統(tǒng)。復方氯丙那林的試藥：鹽酸氯丙那林（純度99.95%，浙江萬邦藥業(yè)有限公司），鹽酸溴己新（純度99.62%，浙江萬邦藥業(yè)有限公司），鹽酸去氯羥嗪（純度99.52%，上海大眾制藥廠），輔料硬脂酸鎂和淀粉為藥用規(guī)格，所有藥品均由蘇州第三制藥廠有限責任公司提供（批號：20050412）。復方對乙酰氨基酚的試藥：對乙酰氨基酚（純度99.73%），阿司匹林（純度100.28%），咖啡因（純度99.38%），輔料檸檬酸、硫尿和淀粉均為藥用規(guī)格，所有藥品均由蘇州第一制藥廠提供（批號：20050209）。

3.2 采集樣品的NIR光譜

分別將樣品粉末直接裝入普通玻璃瓶中，利用積分球漫反射采樣系統(tǒng)測定其NIR光譜。光譜采集條件：以金箔為背景，波數(shù)范圍10000～4000cm-1，分辨率8cm-1，掃描次數(shù)64次，每個樣本以3次實驗的平均光譜作為樣本光譜，以吸收光譜的形式反映樣品組分漫反射光譜的強度。

4 結(jié)果與討論

4.1 樣本的設(shè)計與制備

為了讓定量模型能夠有效地應(yīng)用于實際的復方制劑樣本和對PCA-SVMR方法在復方制劑中的應(yīng)用進行方法學研究，以在復方氯丙那林膠囊和復方對乙酰氨基酚片法定合格含量標準的基礎(chǔ)上并且適當增加可測定范圍為原則，設(shè)計了建立兩種制劑的含量測定模型的樣本集。每類樣本集包含了含量分布均勻的樣本，其中，復方氯丙那林膠囊（30個樣本）為：鹽酸氯丙那林2.80%～4.37%、鹽酸溴己新4.04%～9.91%和鹽酸去氯羥嗪12.60%～19.91%；復方對乙酰氨基酚片（29個樣本）：對乙酰氨基酚25.91%～58.29%、阿司匹林16.05%～28.45%和咖啡因3.59%～6.38%。該文對每類制劑的樣本集中所含的三種有效組分的濃度變化方式進行了非線性設(shè)計，以使樣本間保持線性獨立。

4.2 數(shù)據(jù)處理方法

為了建立兩種制劑的NIRS多元校正模型，所采用的SVM算法軟件為網(wǎng)絡(luò)共享Libsvm軟件（由Chang Chih-chung和Lin Chih-jen提供），該文采用了在MATLAB環(huán)境下運行的Libsvm-MATLAB軟件，而PCA-SVMR軟件則在SVM軟件的基礎(chǔ)上由本實驗室完成。PLS算法的相應(yīng)軟件以及預處理軟件均由本實驗室在MATLAB（V6.0）環(huán)境下編制。

4.3 光譜預處理與富信息光譜波段選擇

在無信號波段明顯發(fā)生了基線漂移，將導致量測數(shù)據(jù)不能準確反映組分的濃度變化，該文以無信息區(qū)間為基礎(chǔ)采用基線平移的方法消除其光譜漂移。

對于波段的選擇，既要保證模型有較好的擬合能力，更要保證模型有較強的預測能力，研究發(fā)現(xiàn)以PLSR方法確定的校正集的交互檢驗的根均方差（RMSECV）最小為標準所選擇的光譜波段，具有最小的預測誤差。基于此確定了兩個樣本集的富信息光譜波段為：復方對乙酰氨基酚片中有效組分對乙酰氨基酚為 7250～7450cm-1和 8600～8980cm-1、阿司匹林 5765～5915cm-1和 6110～6415cm-1、咖啡因 7 940～9620cm-1；復方氯丙那林的三個有效組分均為4000－10000cm-1。

4.4 建立PCA－SVMR多元校正模型

在沒有先驗知識的情況下，用徑向基函數(shù)作為核函數(shù)往往能夠得到較好的擬合結(jié)果[1]，故選擇常用的徑向基函數(shù)K（x，為核函數(shù)[6]。SVMR模型的3個參數(shù)誤差精度ε、正則化系數(shù)C和徑向基核函數(shù)的寬度σ以模型的預測平方相關(guān)系數(shù)最大為標準，采用全局優(yōu)化的方法確定。

為了對PCA-SVMR方法所對立的模型進行方法學考察，選擇了兩種制劑分別建立PCA-SVMR和PLSR多元校正模型。在樣本集中以被測組分的濃度分布均勻為原則，隨機地將其分為校正集和預測集，其中復方氯丙那林的校正集和預測集分別為22和8、復方對乙酰氨基酚則為21和8。利用PCA-SVMR方法建立多元校正模型，其模型參數(shù)見表1和表2。

表1 復方氯丙那林膠囊的PCA-SVMR和PLSR模型

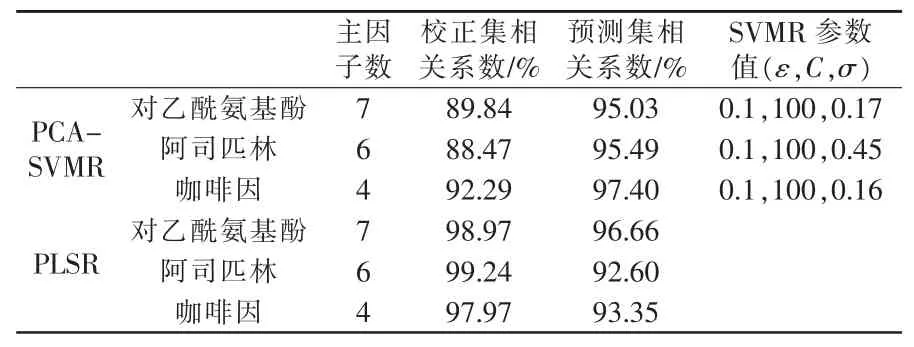
表2 復方對乙酰氨基酚片PCA-SVMR和PLSR模型

4.5 PCA-SVMR方法與PLSR法的比較研究

為了對PCA-SVMR方法在藥物復方制劑中的多組分快速分析測定的特征進行方法學考察與研究，以兩種模型制劑復方氯丙那林與復方對乙酰氨基酚分別考察了該方法與傳統(tǒng)的穩(wěn)健方法PLSR所建立的多元校正模型的模型特征和模型測定的準確度（表1和表2）。為了使兩種方法具有可比性，它們均采用了相同的富信息光譜區(qū)間和主因子數(shù)。從表1和表2可知：PLSR方法具有較強的擬合能力，且強于預測能力，但預測能力嚴重依賴于其擬合能力的強弱，高預測能力的前提是模型必須具有高擬合能力，并且模型的預測穩(wěn)定性也與其擬合樣本的統(tǒng)計特征特別是分布均勻性存在很強的相關(guān)性，建立模型所選樣本的代表性即成為模型預測能力強弱的重要因素或決定因素；對于PCA-SVMR方法，高預測能力并不一定需要高擬合能力為保障，復方氯丙那林的擬合能力略強于預測能力，而復方對乙酰氨基酚的預測能力卻大大強于擬合能力，并且總體上兩種模型制劑的預測能力優(yōu)于PLSR。由于具有這樣的特點，使基于傳統(tǒng)統(tǒng)計學方法的PLSR在藥物小樣本體系中表現(xiàn)出了不穩(wěn)定的特征，此時PCA-SVMR方法卻具有明顯的優(yōu)勢。這樣的特征在藥物生產(chǎn)和臨床藥學中顯得尤為重要，因此該方法在藥物分析中將具有重要的應(yīng)用價值。

[1]瞿海斌，劉曉宣，程翼宇.中藥材三七提取液近紅外光譜的支持向量機回歸校正方法 [J].高等學校化學學報，2004，25（1）：39-43.

[2]Baratieri S C，Barbosa J M，F(xiàn)reitas M P，et al.Multivariate analysis of nystatin and metronidazole in a semi-solid matrix by means of diffuse reflectance NIR spectroscopy and PLS regression[J].Journal of Pharmaceutical and Biomedical Analysis，2006（40）：51-55.

[3]劉平年.PLS法和PCA法在近紅外光譜定量分析中的應(yīng)用研究[J].廣州食品工業(yè)科技，2004，20（4）：106-107，134.

[4]Pérez-Marín D，Garrido-Varo A，Guerrero J E.Nonlinear regression methods in NIRS quantitative analysis[J].Talanta，2007（72）：28-42.

[5]Chauchard F，Cogdill R，Roussel S，et al.Application of LS-SVM to non-linear phenomena in NIR spectroscopy:development of a robust and portable sensor for acidity prediction in grapes[J].Chemometrics and Intelligent Laboratory Systems，2004（71）：141-150.

[6]Vapnik V N.The nature of statistical learning theory[M].北京：清華大學出版社，2000.

[7]張學工.關(guān)于統(tǒng)計學習理論與支持向量機 [J].自動化學報，2000，26（1）：32-42.

[8]國家藥典委員會.中華人民共和國藥典（二部）[M].北京：化學工業(yè)出版社，2005.

[9]康宇飛，瞿海斌，沈 朋，等.預測毛吸管帶電泳有效淌度的支持向量回歸建模方法[J].分析化學，2004，32（9）：1 151-1155.

[10]David Sanchez A V.Advanced support vector machines and kernel methods[J].Neurocomputing，2003（55）：5-20.

[11]王定成，方廷健，唐 毅，等.支持向量機回歸理論與控制的綜述[J].模式識別與人工智能，2003，16（2）：192-197.