淺析既有線平面測繪存在的問題

劉慶修

1 曲線間夾直線太短的處理

我們經常會遇到這樣的情況,在線站交界處或雙線非一次建成的橋梁處,雙線線間距發生變化,即產生最少兩個連續的反向曲線。曲線間無夾直線或夾直線甚短。當能夠確定至少20 m夾直線時(見圖1),第一條曲線沿左軌測量,收斂至 AB,A,B兩點應對鋼軌嚴格分中。由于AB邊太短,則需在B點分中時同時放設遠視點。第一曲線的收斂方向為 A～B的遠視點。第二曲線平面測繪時,則需換側沿右軌自B′點開始進行。由于這種情況下,鐵路兩軌平行性很差,且AB邊太短,如果在換邊時單獨對左右軌分中,則很容易造成第一曲線收斂方向與第二曲線起始方向的不平行,影響平面測繪的連貫性。因此,針對這一問題我們可在換邊時由 A點的分中點垂直鋼軌用小鋼尺量取1 505 mm(取軌距1 435 mm,鋼軌寬70 mm)在右軌上放出 A′點,同樣放出 B′點。這樣則形成矩形 ABB′A′,保證了 AB與A′B′的平行性,置鏡B′后視A′放出遠視點即可開始第二曲線的平面測繪。

當兩反向曲線間不能確定至少20 m夾直線的時候(見圖2),可取夾直線上一點A,作為第一曲線彎道尾,再取 A附近盡量在直線上的一點B(B點可以在A點的前后兩側),AB間距離l為任意(在允許的情況下盡量大),在 A,B點嚴格分中,置鏡 A照準B倒鏡放設遠視點作為第一曲線的收斂方向。采取同樣方法放出B′,A′點,置鏡 A′后視 B′放出遠視點即可開始第二曲線的平面測繪。記錄中顯示第一曲線與第二曲線間就沒有了夾直線,第一曲線的彎道尾置鏡點里程與第二曲線彎道頭置鏡點里程相同。這樣,既解決了平面測繪中換邊引起的丟角、吃角現象,又避免了曲線兩端置鏡點進入曲線范圍內的現象。

2 曲線交叉角的測定

既有線平面測繪中經常會遇到道路、管線與鐵路平交或立交的情況,我們需要量測其交叉角。然而當交叉點在曲線范圍內時,則需要量測曲線切線方向的夾角,相對復雜。曲線夾角的測量關鍵在曲線切線方向的確定(見圖3)。O點為交叉點,我們可以在O點兩側曲線上取等距離L的兩點A,B,置鏡 O,后視 A對180°,倒鏡得 A′方向為 0°,照準 B 讀數 α,則得 α/2方向即為O點處曲線的切線方向。如兩交叉線路均為曲線,用同樣方法分別確定其切線方向,即可得兩線的切線夾角。

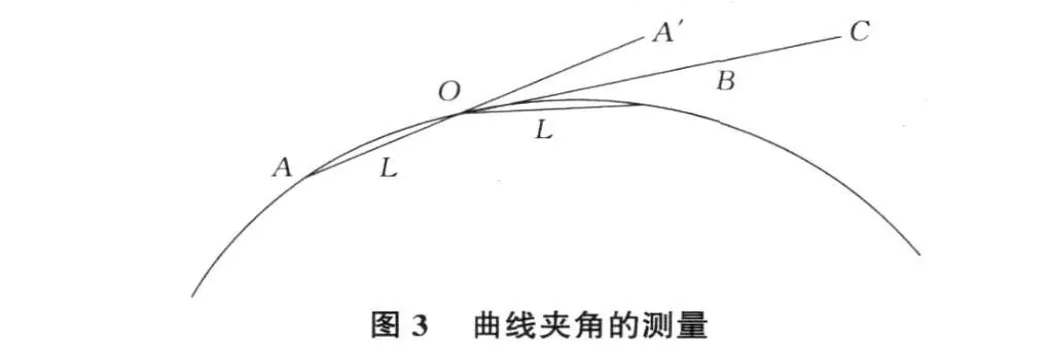
3 道岔轍岔角的測量

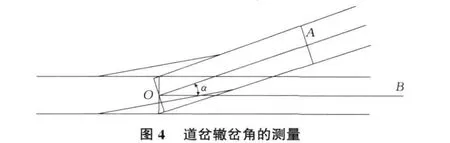
道岔轍岔角的測量相對簡單(見圖4),只需置鏡岔心O,對岔后兩方向股道分別分中,測得角α即為轍岔角。在此值得一提的是,當OA方向為專用線需進行平面測繪,且岔后直線相當短,轍岔角作為與正線聯關系的角,需股道分中測量,專用線岔后曲線測繪需置鏡外軌,由于岔心O處OA方向為曲線軌,不能對鋼軌直接分中得到后視點,則需先在 A點處對應鋼軌精確分中得A′,量取鋼軌分中點至股道分中點的距離,再以相同的距離從岔心O垂直鋼軌確定理論鋼軌分中點O′,使得 OA平行于O′A′。

4 橋梁凈空和電線垂度等的測量

橋梁凈空和電線垂度的測量有很多種方式,如測高桿直接量取法、釣魚法、三角法等。這里我們著重研究三角法,即通過實測置鏡點O到測高點A的平距d和豎直角θ,由三角函數計算出高度h。由于橋梁凈高和電線垂度有時控制設計,所以要求精度很高。而測量精度的高低實際取決于測距時棱鏡所立位置與測高點的偏差大小。因此,在確定測高點位置時應相當謹慎。為減小誤差,也可盡量增大置鏡點到測高點的距離以減小豎直角。目前有一些全站儀如捷創力系列等,具有懸高測量功能,可直接讀出懸高,但在使用時應特別注意棱鏡高問題。

5 平面聯關系時應注意的事項

平面測繪與GPS點聯測時,應注意聯測至股道分中點。

在閉合段落兩端分中聯關系時,為了避免兩條鋼軌不平行性的影響,分中點均應由置鏡的一側鋼軌分中點量出。

6 左右線聯關系時應注意的事項

當鐵路左右線并行時,一般沿左線進行平面測繪,右線只測曲線,左右線利用線間距發生關系。但隨著鐵路等級的不斷提高,這樣已滿足不了測量精度要求。如京秦沈電氣化改造項目中,即要求右線曲線平面測繪閉合于左線。這時,按理論應對左右線分中進行聯測。但由于左右線平行,且均沿同側鋼軌進行平面測繪,根據平行移動的原理,則無須分中,可在同側鋼軌上直接聯關系。這樣不僅起到相同的作用,而且減少了股道分中的誤差的影響。這種聯測方法雖然保證了精度、提高了作業效率,但僅限于左右線平行的條件下使用。在左右線不平行時,還應對左右線嚴格分中進行聯測。

7 平面測繪帶百尺標測量的作業方法嘗試

百尺標丈量是一項占用人員較多的作業項目,且精度受限制,無法大幅度提高,而平面測繪的精度要求不斷提高,造成作業精度不相匹配的問題。鑒于此,我們在大鄭線等項目中,嘗試采用了平面測繪帶百尺標測量的作業模式。即在長大直線段,采用全站儀直接在鋼軌上測定百尺標,同時進行平面測繪。由于將兩個作業組合并為一個作業組,且可用全站儀往返測距檢核百尺標,無需二鏈復核,節省了人員。全站儀測定百尺標精度大大高于鋼尺拉鏈,可提高平面測繪閉合精度。

[1] 秦 珂.淺析現代測繪技術的發展趨勢[J].山西建筑,2008,34(23):358-359.