對UC模型傳統假定的再檢驗——基于中國GDP的實證

蔡經漢

（華僑大學 商學院，福建 泉州 362021）

0 引言

不可觀測成份（Unobserved Component，UC）模型將一個時間序列分解成永久與暫時兩個不可見的成份。傳統上，大部分關于UC模型的文獻都使用了兩個假定：（1）永久性成份(也稱趨勢項)是隨機趨勢，通常表現為一個隨機游走序列，這個成份一般用于代表潛在產出；暫時性成份(也稱周期項）是一個平穩的ARMA過程，這個成份一般用于代表產出缺口。（2）永久性成份及暫時性成份各自所面臨的沖擊之間是不相關的,該假定可簡稱為零相關假定。通常，這個零相關假定的使用并不是非常合理的，雖然在某些情況下是由于模型識別的需要，但主要仍是為了簡化模型，使模型易于處理。在中國，到目前為止，一般都使用了這個零相關假定。趙留彥（2006）在估計產出缺口和核心通脹的二元UC模型中，也使用了零相關假定，他認為該假定是模型可識別的必要條件。事實上，下文將說明，就其所使用的模型設定而言，該零相關假定并不是模型識別的必要條件。相反地，這樣一個約束條件可能扭曲對趨勢項和周期項的估計。在最近的文獻中，如Morley,Nelson,Zivot(2002)，Nagakura（2007）等，論證了該假定的不合理性，即：其對于模型識別并不是必需的，而且也被數據所拒絕。進一步，與零相關假定相對的，他們估計出的相關度都是高度負相關的，至少在-0.7到-1之間，在某些情況下甚至非常接近-1。這些結果與BN分解非常相似。作為其必然的性質，BN分解中分解出來的長期沖擊與短期沖擊序列是完全負相關的，相關系數為-1。Morley,Nelson,Zivot（2002）在將UC分解與BN分解進行比較后發現，該零相關假定可能是有問題的。他們在UC模型中允許長期沖擊與短期沖擊項之間的協方差不為0，即允許σηε≠0（或者說，是沒有對UC模型施加σηε的約束），此無約束的UC模型與BN分解的結果是相同的。并且，他們估得相關系數ρηε=-0.9062，即高度負相關。此時，GDP序列的波動主要由趨勢項產生，而周期項是類似于白噪聲的干擾項。零相關假定是否成立，對于UC模型而言是非常重要的。如果零相關假定成立的話，那么從總體序列中分離出來的兩個序列中，總體的變化主要由暫時的周期項序列的變化產生。也就是說，產出的變化主要是由于產出缺口的變化而產生，是短期的因素。但如果零相關假定不成立的話，那么，總體的變化主要由永久的趨勢項產生。那就意味著，產出的變化是由于真實經濟沖擊而產生的，對名義量如貨幣供給等進行控制的重要性就減弱了。本文采用Morley,Nelson,Zivot以及Nagakura的方法對中國 GDP季度數據的時間序列做相應的實證分析，發現結果是否定零相關假定的。本文的結果顯示，與美國及其它發達國家相類似，對中國而言趨勢項與周期項的沖擊之間也是高度負相關的。

1 模型

1.1 UC模型

本文采用的UC模型如下（yt為真實GDP的自然對數值）：

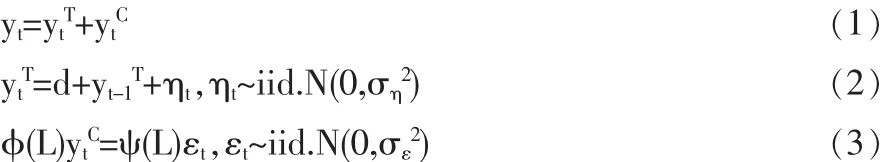
1.2 UC模型的ARIMA誘導式（reduced form）

如上的一個UC模型所表示的{yt}，因為其周期項為一個ARMA(p,q)過程，通常就記為UC-ARMA（p,q）過程。這樣的一個{yt}可以表示成一個ARIMA過程，推導過程如下：

對式（1）作差分，得

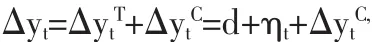
即(1-L)yt=d+ηt+(1-L)ytC，兩邊同乘以 φ(L)，由 Hamilton(1994)，得

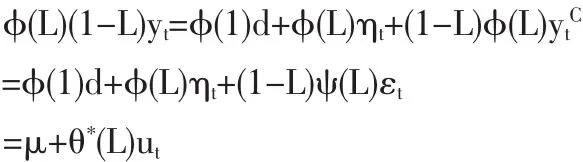
根據檢驗發現，△yt～ARMA(2,2)， 即 yt～ARIMA(2,1,2)，q*等于 2，因此可設定

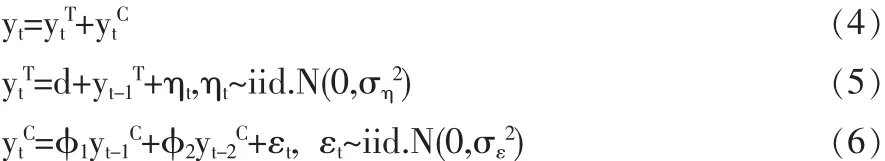
則有

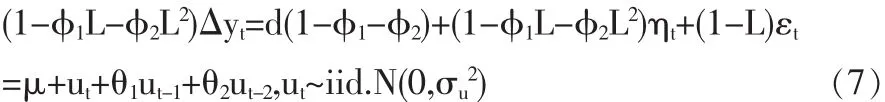
由上式第二個等式，右側的自協方差可求為

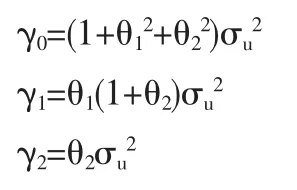
由上式第一個等式，右側的自協方差可求為

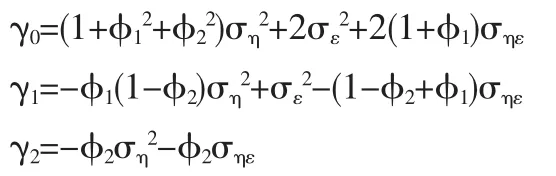
兩者是等同的，因此有

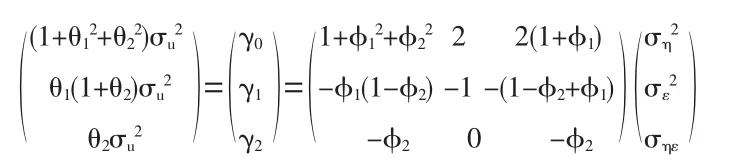
即

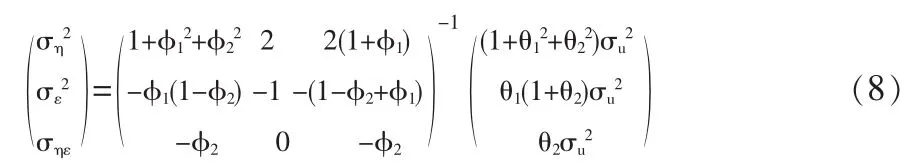
（7）式估計后得到 φ1,φ2,μ,θ1,θ2,σu2的估計值，代入（8）式中即可求得的估計值。

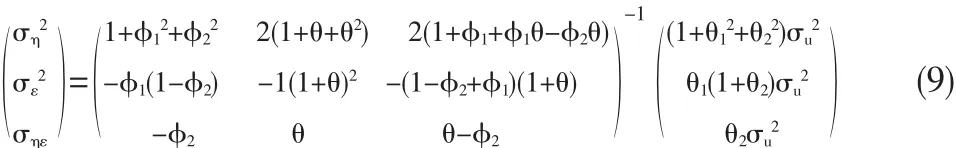
當限定 θ=0 時，（9）式即還原為（8）。 （9）式有四個未知數，但只有三個方程，因此沒有唯一解。事實上，此時模型面臨著一個識別的問題。所以我們必須對θ施加約束（UC-AR(2)模型事實上就是施加了θ=0的約束），若設定θ等于某個固定值，則上式就將有唯一解。因為我們并不能確切地認定是否有θ=0，所以本文將分別討論這兩種情況。

1.3 識別問題

從UC模型的原始形式到誘導式之間，存在一個識別問題。由原始形式可以唯一地確定一個ARIMA誘導式，但由ARIMA誘導式卻不能唯一地確定原始形式。當我們估計出誘導式之后，需要某些約束條件，以得到唯一的原始形式。但要非常小心的是，對于最后分解出來的趨勢項及周期項而言，其特征對所使用的約束條件是非常敏感的。

傳統上采用的約束條件是趨勢項與周期項的沖擊之間設定為零相關，但這個約束條件正如本文之前所言，更多的是出于簡化的需要，而非絕對的必要。這個條件事實上是對模型的ARIMA誘導式施加了一個非線性的約束，不使用這個約束條件是可以的。在這種情況下，對于一個I(1)的UCARMA(p,q)來說，其識別條件是 p≥q+2。 如（8）式所示，p≥q+2保證了有足夠多的自協方差可以用來計算和求解。所以如果我們設定p=2，則識別條件要求q=0，否則無法識別，在本文的情況下即為要求模型為UC-AR(2)。但UC-ARMA（2，1）也是可能的，此時即為q=1。在q=1的情況下，多了一個參數θ（見（9）式），這個參數使得模型變成無法識別。在這種情況下，可以設定這個參數θ。在某個區間上采取類似網格的方法來設定θ，每一次設定之后，系統都是將是可識別的，并且可以計算出沖擊的相關系數ρηε。最后事實上就得到了一個θ與ρηε之間類似于函數的關系。

2 實證結果

2.1 數據

本文所使用的GDP數據是從中經網數據庫獲得。該數據庫僅提供累計GDP，經處理后得到名義季度GDP序列。除以價格水平后，得到真實季度GDP序列，然后進行季節處理并取對數，得到最后使用的數據。數據的時間為1993年第一季度到2007年第三季度。

2.2 無約束的ARIMA(2,1,2)模型及相應UC-AR(2)模型的參數估計結果

首先估計{yt}的ARIMA(2,1,2)模型。隨后，計算對應的UC-AR(2)模型中的參數。估計結果如表1。

表1

根據（8）式，可得 ση2,σε2,σηε的估計值，及相應的 ηt與 εt之間的相關系數ρηε如表2。

ηt與εt顯示出高度的負相關。

根據 Lippi和 Reichlin（1992），若 σηε=0，則 A（1）=θ*（1）/φ（1）應小于等于 1。 若大于 1，則相當于否定了 σηε=0的可能。 進一步，Nagakura 和 Zivot（2007）證明，若 A（1）2≥1，則應有 ρηε<0。 根據以上各參數的估計結果可算出 A（1）=1.0952。這進一步顯示，ηt與 εt確實應為負相關。

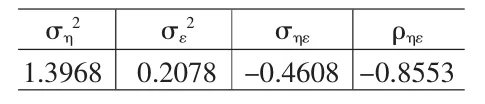
表2

2.3 UC-ARMA（2，1）模型中θ與ρ的對應關系結果

如上文所述，在 UC模型的誘導式是 ARIMA（2，1，2）的情況下，ytC既可能是AR(2)也可能是ARMA(2,1)。只要θ=0就可以從ARMA（2，1）得到AR(2)，這相當于設定了一個約束條件。但是否有θ=0則要看實證結果。Nagakura（2007）對西方七國集團除日本外其余六國的研究表明，除了美國和法國，其他國家都不支持θ=0（θ=0時所隱含的ρ超出了ρ作為相關系數所應處于的區間范圍，即應有-1≤ρ≤1）。本文依同樣的思路檢查中國的情況，結果圖1所示。

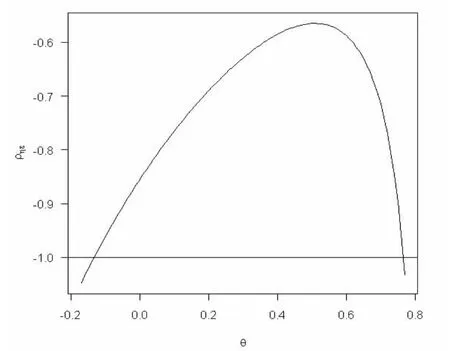
圖1

首先，就中國的情況而言，并不能拒絕θ=0。因為-1≤ρ≤1，我們可確定θ所應處的范圍，即大約有-0.14≤θ≤0.76。 其次，雖然對于不同的 θ有不同的 ρηε，但可以看到，ρηε存在一個最大值-0.565，因此，即使我們不能確定模型究竟是UC-AR(2)還是UC-ARMA(2,1)，我們仍然可以肯定一點，即ρηε是一個負數，并且就其大小而言，可以認為ηt與εt之間是高度負相關的。

3 結論及分析

本文利用Morley,Nelson,Zivot以及Nagakura的方法驗證了中國的真實GDP的一元UC模型中長期項與短期項的沖擊之間存在著顯著的負相關。當模型是UC-AR(2)時，相關系數是-0.8533，而當模型是較為不確定的UC-ARMA(2,1)時，相關系數仍存在一個上界-0.565。因此，本文得出的結論是ηt與εt之間是高度負相關的。

這個結論否定了在UC模型中長期使用的零相關假定。接受這個結論意味著在宏觀經濟中真實沖擊的影響應該是比較重要的。正如Stock和Watson（1988）中指出的，真實沖擊趨于提高產出的長期路徑，而短期波動在很大程度上反映出當真實沖擊扮演統治地位時經濟所作出的調整：趨勢項的一個正的沖擊往往與同期的周期項的一個負的沖擊聯系在一起。例如，當生產率有一次提高的時候，產出的長期路徑將立刻向上提升，實際產出此時將位于產出趨勢之下，直到在經歷了一個調整過程之后趕上趨勢為止。

本文的研究結論意味著，在以往針對中國產出的UC模型的建模可能是有問題的。我們將在今后的研究中重新審視以往的建模，在新的條件下，期望得到新的結果。

[1]趙留彥.中國核心通脹率與產出缺口經驗分析[J].經濟學（季刊），2006.

[2]Morley,J.C.,Nelson,C.R.,E.Zivot.Why are the Beveridge-Nelson and Unobserved Components Decompositions of GDP so Different?[J].The Review of Economics and Statistics,2003，85.

[3]Nagakura,D.Inference on the Correlation between Permanent and Transitory ShocksforUnidentied Unobserved Components Models[C].University of Washington,Working Paper，2007.

[4]Hamilton D J.Time Series Analysis[M].Princeton,NJ:Princeton University Press，1994.

[5]Lippi M,Reichlin L.On Persistence of Shocks to Economic Vari ables:a Common Misconception[J].Journal of Monetary Economics，

1992，29.

[6]Nagakura,D,Zivot,E.Implications of Two Measures of Persistence for Correlation between Permanent and Transitory Shocks in U.S.Real GDP[C].University of Washington,Working Paper，2007.

[7]Stock,J H.,M.W.Watson.Variable Trends in Economic Time Series[J].Journal of Economic Perspectives，1988，2.