實現相關系數模型：基于動態相關高頻Bi-GARCH過程的MC檢驗

殷煉乾 ，周雨田 ，2，3

（1.西安交通大學 金禾經濟研究中心，西安 710049；2.臺灣中研院 經濟研究所，臺北；3.新竹交通大學 商管所，臺北）

0 引言

在投資學和風險管理的理論和實踐中，資產組合配置是否有效依賴于組合資產的相關系數，尋找最優的對沖比率更是需要精確估計對沖資產的相關系數，而想要精確地計算大型資產組合在險價值，則最好使用各資產相關系數的動態估計值。盡管得益于Engle和Granger等人為代表的研究，波動率模型自上世紀90年代起就開始被大量發展出來，但是由于多元波動率模型的設定和估計技術都十分復雜，相關系數模型的估計精度也難以得到實證支持。本文正是在這樣一個背景下試圖對這一問題做出一些研究和探索。

本文擬通過構建具有不同動態相關模式的高頻Bi-GARCH模型作為資產收益的代表，對實現相關系數模型捕捉變動金融資產價格相關系數的能力和其他方法進行蒙特卡洛比較，以期證明該方法的改進與資產收益的相關系數變化方式有關：當金融市場相對平穩、資產間相關系數比較穩定時，此類方法并不明顯地優于其它方法；然而當金融市場中發生較為劇烈的變化，導致資產間相關系數快速變動時，此類方法卻能夠大幅提高相關系數的估計精度。

1 模型

考慮一個包含N個資產的對數價格向量Pt=(p1,p2,…pn)，假設它服從一個多元連續時間的一般維納過程：dPt=μtdt+ΩtdBt，其中μt表示漂移向量，Ωt表示一個N×N維的正定擴散矩陣，Bt表示一個N維的標準布朗運動，定義這N個資產的在時間長度h內的收益率向量為rt+h,h≡Pt+h-Pt，則這一收益率的分布為其中，表示σ域從0≤τ≤h的時間內產生的μt+τ和Ωt+τ的樣本路徑。因此這個積分形式的擴散矩陣給h期內的真實波動率提供了一個很好的估計方法。根據二次方差理論，我們有0，即在一些弱正則條件下，Ht+h幾乎一定收斂于h時間長度的真實波動率具體參見 Fleming,Kirby 和 Ostdiek(2003)[19]。因此，我們可以使用日內收益率來構造積分協方差的非參數估計量。做樣本外預測時，我們為Ht+h配置一個簡單的隨機漫步模型（RCRW模型），為的是能讓這樣一個非參估計能夠方便的擴展到N維（N>>2）的情況，并應用到實際中去。假定上述的時間長度h為單位時間1天，并定義第t天的已實現協方差矩陣為為一天內觀察到高頻數據的在特定頻率下取樣的筆數，比如說5分鐘數據在我國股市中一天就有n=48筆數據，則模型為：Ht+1=Ht+εt，即簡單地使用第t天的實現協方差矩陣的估計作為第t+1天的預測值，也就是：E[Ht+1｜It]=E[Ht+εt｜It]=E[Ht｜It]=（Ht，其中It表示到時點t為止的信息集。在得到預測的實現協方差矩陣后，使用資產間實現協方差和資產方差之比就可以得到實現相關系數，這一實現波動率隨機漫步模型也被稱作為實現相關系數模型。

與RCRW模型的第一個對比模型是歷史數據滾動法，因其原理和操作都簡單易懂而被業界廣泛使用，在本文的二元環境中，上式中相關系數的估計可以表示為：

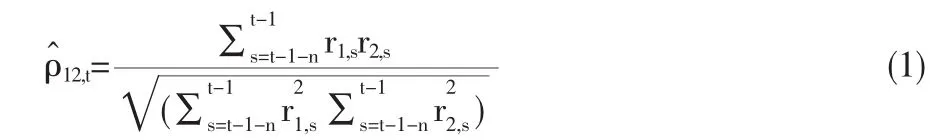
我們在本文中采用100天的時間窗口，即式中的n=100。第二個模型我們使用普通的指數平滑法和已實現波動率作比較在本文的二元環境中，上式可以表達為：

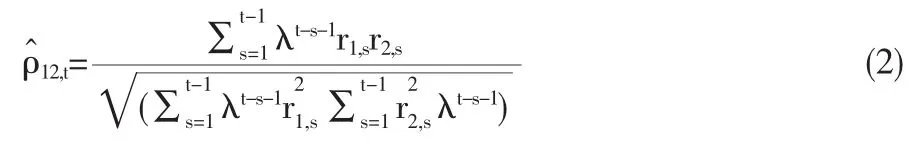
我們在本文中采用業界通用標準，即使用的標準。以上兩個模型都因技術簡單而較易擴展到多維情況，然而它們的估計精度卻很低。第三個模型我們采用較為復雜的技術，即Alexander提出的正交化GARCH模型，簡單的講即找到協方差矩陣的Cholesky Decomposition形式其中 Lt是一個下三角矩陣，Gt是對角矩陣是日收益率向量rt的一個線性組合，它的協方差矩陣為這一形式的優越性在于Lt和Gt可以通過簡單的線性回歸式得到，在本文的二元環境中，相關系數的估計式可以表達為：

σ11,t是r1在t期的動態均方差，可以使用一個單變量的GARCH模型得到，而βt和分別是下面線性回歸式的系數和殘差的平方：

本文中我們對（4）式的殘差采用一個GARCH模型的設定來代替以得到βt和更好的估計值，即假設存在以下異方差形式經過上式調整過的得到的動態相關系數會比原來的簡單正交化GARCH好。

2 動態相關的高頻Bi-GARCH模型

我們采用Engle中的方法，測試模型在蒙特卡羅試驗中的表現。考慮T個交易日，把每天的4個小時的營業時間劃分為m個等間距的時間長度，那么第t天的第j筆日內收益率可以表示為rt+j/m，由于日內收益率相對其波動率來說非常小，因此設它的均值為0。令日內的數據產生機制(DGP)為兩個相互關聯的過程：

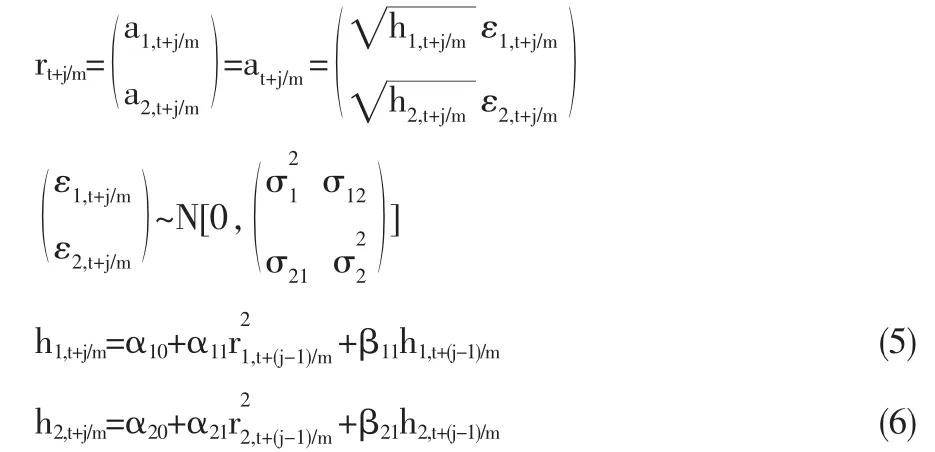
其中有：t=1，2，…，T 和 j=1，2，…，m。 為保證此過程的平穩性，我們限定 α0>0，α1>0，β1>0 和 α1+β1＜1。 為保證協方差矩陣的正定性，限定σ12=σ21≥0。為了和我們的實證結果相對比，我們在模擬中也采用五分鐘頻率數據，即1≤j≤48，m=48，并模擬1000個交易日的時間長度。我們將(5)式設定為一個高度持久的 GARCH （1，1） 過程：α10=0.01，α11=0.05,β11=0.94；將(6)式設定為一個普通的 GARCH(1，1)過程：α20=0.5，α21=0.2,β21=0.5。對于此數據產生機制中的每日相關系數ρt=σ12/σ1σ2， 我們將之設定為 5種情況：(1)恒定的相關系數 ρt=0.9；(2)正弦變化的相關系數 ρt=0.5+0.4cos(2πt/200)；(3)快速正弦變化的相關系數ρt=0.5+0.4cos(2πt/20)；(4)階段變化的相關系數 ρt=0.9-0.5I(t>500)，I（t>500）=1，I（else）=0；(5)坡度變化的相關系數ρt=mod(t/200)。這樣，我們就得到5對具有不同動態相關系數的數據，每一對由兩個GARCH(1，1)過程組成，其中每一個GARCH（1，1）有1000個交易日每天48筆數據，共48000筆數據。

3 測試結果

我們在這一小節采用絕對值誤差均值，就是真實相關系數和模型得到的相關系數數值之差的絕對值之平均值，定義為很明顯具有 MAE 最小值的模型最優。表1給出了五種不同相關系數下四個模型的MAE數值，其中RCRW表示隨機游走的實現相關系數模型得到的估計值，HRMA表示歷史滾動移動平滑法，即由（1）式得到的估計值；EX06表示采用λ=0.94的指數平滑法,即由（2）式得到的估計值；OGARCH表示Orthogonal GARCH模型，即由（3）式得到的估計值。

從表1中可以清楚地看到，無論作為資產收益代表的高頻動態相關Bi-GARCH過程呈現出什么樣的相關變化模式，使用實現波動率矩陣構建的隨機游走實現相關系數RCRW模型總是可以給出最準確的估計值。然而，同時我們也注意到，使用RCRW模型所得到的改進大小也是依賴于相關系數的變動模式的：（1）當兩類資產收益之間的相關系數較為穩定的時候（比如當雙GARCH過程的相關系數恒定或呈階段模式變動時），RCRW并沒有顯著的改進其他模型的估計，四類模型所得到的MAE值都相差不大；（2）當資產收益間的相關系數極度不穩定，變動速度較快的時候（比如這兩個過程相關系數呈正弦，快速正弦和坡度變動），使用實現波動率矩陣構建的RCRW就能夠大幅度的提高相關系數的估計精度。

表1 四種模型在五種動態相關系數下的MAE數值

4 結論

本文使用蒙特卡洛隨機模擬技術，構建了具有不同動態相關模式的高頻Bi-GARCH模型對作為金融資產收益序列，以測評各類模型對相關系數的估計精度。在此框架下，本文將使用多元實現波動率矩陣構建的RCRW模型和其他類別的相關系數模型作了對比研究。研究發現，雖然該方法能夠普遍改進模型的估計精度，但改進的程度依賴于資產間相關系數的變化模式：當金融資產價格相關系數恒定或相對穩定時，此類方法并不明顯優于其它方法；然而當資產價格相關系數快速變動時，此類方法能夠大幅提高估計精度，明顯地優于其它方法。 這說明實現相關系數模型在金融市場發生劇烈快速波動時較其他方法更為有效。

[1]魏宇,余怒濤.中國股票市場的波動率預測模型及其SPA檢驗[J].金融研究,2007,325(7).

[2]殷煉乾,周雨田.中國金融市場波動率的實現極差雙冪次變差估計[J].統計與決策，2009，3(43).

[3]邵錫棟，殷煉乾.基于實現極差和實現波動率的中國金融市場風險測度研究[J].金融研究2008(06).

[4]邵錫棟,黃性芳,殷煉乾.多變量隨機波動率模型及在中國股市的應用[J].統計與決策，2008,18(32).

[5]Epps T W.Comovements in Stock Prices in the Very Short Run[J].Journal of the American Statistical Association,1979,74(366).

[6]Bollerslev,T,R.Y.Chou,K.F.Kroner.ARCH Modeling in Finance:A Review of the Theory and Empirical Evidence[J].Journal of Econometrics,1992,52(1).

[7]Alexander C.O.Orthogonal GARCH[C].C.O.Alexander,Mastering Risk,Volume 2,Financial Times,U.S.A.,Prentice Hall,2001.

[8]R F Engle.Dynamic Conditional Correlation:A Simple Class of Multivariate GARCH Models[J].Journal of Business and Economic Statistics，2002，22(3).