為何繩端速度如此分解

方銀良

(浙江省衢州二中,浙江衢州 324000)

用輕繩相聯系的“兩體”是高中物理常見的一種理想模型,這一類“兩體”問題經常會涉及到“輕繩末端速度”的分解,這是高中物理教學中一個難點.很多資料在介紹速度分解法時,一般就明確告知學生此類問題要按運動的實際效果分解,或沿繩子方向和垂直于繩子方向分解,而沒有說明為什么要如此.對此學生知其然而不知其所以然,只能死記,沒有真正理解.下面筆者根據自己的教學經驗,從例題入手,經發現問題、提出問題、突破難點、例題解析、問題辨析等幾個方面一步一步地展開分析討論,讓學生理解為何要把繩端速度如此分解.

例.如圖1,甲小車在高臺上通過不可伸縮的輕繩拉動地面上的乙小車,甲車以速度 v0做勻速直線運動,當傾斜繩子與水平面夾角為θ時,求乙車的速度v.

分析:乙車的運動是由于繩子的牽引作用,但乙車并不沿繩子收縮方向運動,它沿水平方向運動.設甲車拉繩子速度v0(即沿繩子方向速度)為牽引速度,很明顯乙車的速度不等于繩子牽引速度v0.要求乙車速度,一定得從繩子運動入手,那么兩者速度到底有什么關系呢?分析繩子上的點,傾斜部分繩子上的各點的運動不沿繩子收縮方向(如B點沿BB′運動,A點沿水平面運動),所以其上各點的速度是不一樣的,也不等于繩子牽引速度 v0,但由于繩子的不可伸縮性,傾斜部分繩子上點的速度在繩子上的投影都等于牽引速度v0.設繩子與乙車的接點為 A,則整根繩子上,只有A點的運動才是反映乙車的運動.那么 A點的速度是多少呢?

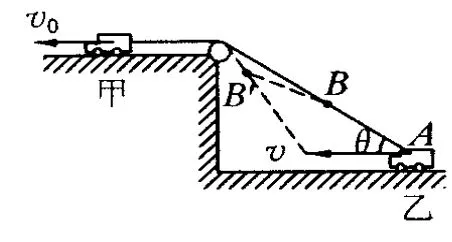
圖1

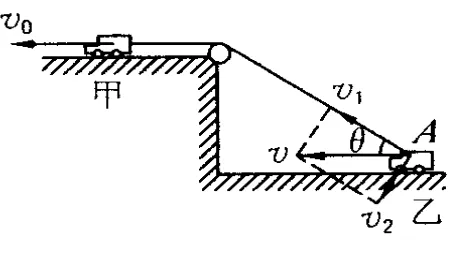
圖2

現在我們就來研究接點A的實際運動.A點水平向左運動,可以看成如下兩個分運動的合成:一個沿繩子方向v1,一個垂直于繩子方向 v2(如圖2).兩分運動產生兩個效果:v1的作用是使繩子收縮,v2的作用是使繩子轉動.因為垂直繩子方向的速度 v2對繩子收縮沒影響,故分速度v1與繩子牽引速度相等,即v1=v0,由平行四邊形定則可得此時乙物體的速度大小為

對于上面的分析,學生有疑惑:A點運動為何一定要按圖2方向分解?沿其他方向分解不行嗎?

從理論上講,一個矢量不論是力、加速度、位移還是速度,都可以分解為無數對大小和方向不同的分矢量,而不像兩矢量合成那樣具有唯一性.一個實際的運動跟它的分運動形式無關,只要分運動的合成是唯一的合運動.即每一個分運動可能產生的影響可以不同,但所有分運動對物體總的影響是不變的.比如斜拋運動的分解,可以分解為豎直方向的勻變速直線運動和水平方向的勻速直線運動;也可以是豎直方向的勻變速直線運動和初速方向的勻速直線運動;還可以是沿初速方向的勻變速直線運動和垂直初速方向的勻變速直線運動等.

對于上述 A點的運動,也應該有多種分解方式.現在按圖3來分解,v3沿繩子方向,v4豎直向下.分析兩分速度的影響:因為 v4的作用既使繩子轉動,又使繩子伸長,它對繩子的收縮起作用,故分速度v3雖沿繩子方向,作用是使繩子收縮,它的大小卻與繩子牽引速度v0不相等.它們具體關系滿足v3-v4sinθ=v0,又因為 A點實際是水平運動,故 v3sinθ=v4,而乙物體的速度大小 v=v3?cosθ,由以上可得結論是一樣的.

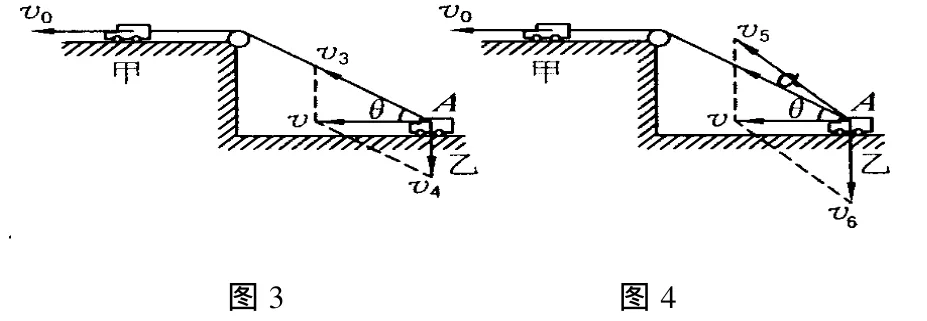
又如按圖4分解,v5方向與傾斜繩子的夾角為α,v6豎直向下.這時兩個分速度對繩子的收縮和轉動都起作用.因為繩子被牽引速度大小是不變的,可得方程 v5cosαv6sinθ=v0;又因為 A點水平運動,故 v5sin(α+θ)=v6,v=v5cos(α+θ).由以上方程可得結論還是一樣的.

綜上所述,一個合運動的分解方式應該是無數的,只是不同方法的解題難易差別很大.對于理想繩子端速度的分解,主要應理解兩點:一是繩子上各點的速度在繩上的投影是一樣的;二是弄清繩端的運動實際方向,即合運動的方向.繩端運動的分解可以任意,但要考慮清楚每個分運動產生的影響.如按圖2方式分解,兩分速度相互垂直,它們所起的影響相互獨立,所列方程比較簡單.而若按其他方向分解,那么各分速度的作用相互牽扯,列出的方程就比較復雜.所以,繩端速度分解一般沿繩子方向和垂直于繩子方向.

實際上,對于所有矢量的分解都是一樣,總是選取對解決問題最方便的分解方式.