分層粗糙面下方介質目標散射的快速算法

姬偉杰 童創明,2

(1.空軍工程大學導彈學院,陜西 三原 713800;2.毫米波國家重點實驗室,江蘇 南京 210096)

1.引 言

目標與地、海背景的復合電磁散射研究在現代雷達探測、海洋遙感和目標隱身技術中有著重要的意義,該研究一直是電磁散射領域較為復雜的課題,引起了諸多學者的興趣[1-13]。例如：文獻[1]中計算了無限大介質平板上介質目標的電磁散射,文獻[2]中運用FBM/SAA研究了低掠角入射時一維分形粗糙面和二維艦船目標的雙站散射,而WANG X等用傳統矩量法研究了一維粗糙面目標的復合散射[3],YE等研究了一維粗糙面與上方金屬目標的差場散射截面[4],同時研究了計算三維目標和粗糙面的數值-解析混合算法[5]。王運華等基于互易定理和矩量法研究了平面上方二維介質目標對高斯波束的電磁散射[6],王蕊等也研究了一維海洋粗糙面上方金屬目標的混合算法[7]。然而,大多數學者都只研究單層粗糙面和目標的復合散射,只有少數學者研究了分層粗糙面和目標的復合散射。文獻[8]中,KUO等應用周期擴展法(EBCM)計算了一維分層粗糙面與下方目標的復合電磁散射。文獻[10]中,CHEW W C等研究了分界面是平面的分層媒質上方目標的散射。然而,上述算法受粗糙面與目標參數的限制,只適用于計算粗糙度較小的粗糙面和電小尺寸目標的復合散射。同時,上述研究都將目標和分層目標一起看成一個組合散射體,電磁表面積分方程離散后產生了巨大的未知量,對計算機硬件和編程提出了很高的要求,很大程度上限制了數值算法的應用。

在分層粗糙面與目標的復合散射計算中,粗糙面的未知量占絕大部分,因此,如何快速計算分層粗糙面的電磁散射顯得尤為重要。近年來發展的前后向迭代法(FBM)[14]非常適合于計算粗糙面這類散射問題,在文獻[15]中,MOSS C D等進一步將其應用于計算分層粗糙面的電磁散射特性,該方法對不同參數的分層粗糙面都具有良好的收斂性和準確性。

基于分層粗糙面與目標復合散射的物理機理,結合FBM和雙共軛梯度算法(Bi-CG),提出一種計算一維分層介質粗糙面及下方介質目標的復合電磁散射的快速互耦迭代數值算法(CCIA)。推導了目標與分層粗糙面的耦合邊界積分方程,分層粗糙面部分的邊界方程用FBM求解,目標的邊界方程用Bi-CG求解,粗糙面與目標的相互作用通過不斷更新矩陣方程的激勵項來實現。該算法的計算量為O(N2),較之傳統矩量法計算效率大為提高。其計算結果與傳統矩量法得到的結果相一致,驗證了該方法的準確性。最后,計算了粗糙度較大的分層粗糙面和電中尺寸介質目標的復合散射系數,討論了目標尺寸和位置變化對雙站散射系數的影響。

2.基本理論

2.1 一維分層粗糙面與下方介質目標的耦合邊界積分方程

考慮無限長介質圓柱位于一維雙層介質粗糙面下方,如圖1所示。為區域i中的介電常數和磁導率(i=0,1,2,3),其中,i=0表示分層粗糙面上方自由空間,i=1,2表示分層粗糙面下方介質空間,i=3表示目標所占區域。目標表面用fc表示,粗糙面用(x)表示(i=1,2分別表示上層和下層粗糙面)。ψinc表示入射波,為區域i中的總場(i=0,1,2)。

圖1 雙層粗糙面下方介質目標的示意圖

根據文獻[15]-[16],沒有目標時,分層粗糙面的邊界積分方程為

當分層粗糙面下方存在介質目標時,方程(2)應該為

上式左邊第三項表示目標的散射場,且在目標內部有邊界積分方程

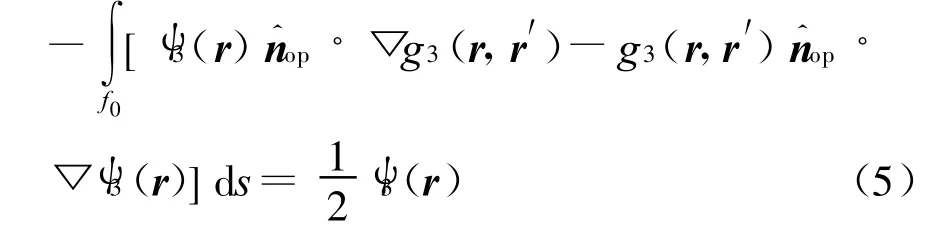
這樣,方程(1)、(3)、(4)和(5)共同構成分層粗糙面與下方介質目標的耦合積分方程組。其中,r表示場點表示源點,gi(r,表示各區域的二維格林函數。表示第i個粗糙面的單位法向向量,方向朝上,表示目標表面法向向量,方向由目標內向外。TE波粗糙面邊界條件為：介質目標的邊界條件為波的邊界條件可由二元性原理獲得。

用MoM求解分層粗糙面與介質目標復合電磁散射時,得到的阻抗矩陣大小完全取決于分層粗糙面的長度和目標尺寸大小以及采樣點的多少。因此,對大尺寸分層粗糙面和目標,直接用傳統MoM求解,需要求解維數為4×N+2×M的線性方程組,當粗糙面長度較大時,未知量往往成千上萬,要直接求解是比較困難的。鑒于此,本文提出一種互耦迭代算法求解分層粗糙面與目標的復合電磁散射,該算法在考慮了分層粗糙面與目標相互作用的基礎上,對分層粗糙面表面積分方程用FBM求解,對目標表面積分方程用Bi-CG求解,通過迭代求解方程組。計算量和內存減少為O(N2),很大程度上提高了計算效率,克服了傳統MoM的局限性。

2.2 互耦迭代算法(CCIA)

對方程(6)進行整理,可以得到如下矩陣方程組

式中：(7a)表示的是求解分層粗糙面表面電流分布的矩陣方程,(7b)表示的是求解目標面流分布的矩陣方程。其中,表示目標對上層粗糙面的入射場貢獻,ψ0為目標對下層粗糙面入射場貢獻,ψSur=-F(1)?U1-H(1)? ψ1-I(2)?U2-J(2)? ψ2,前兩項表示上層粗糙面對目標的散射貢獻,后兩項表示下層粗糙面對目標的散射貢獻。可見,對分層粗糙面不僅有上方入射波的照射,還有下方目標對它的影響,對下方目標的照射波為粗糙面的透射波,分層粗糙面與目標的相互作用正是通過不斷更新右邊的激勵項來實現的。

對方程組(7)采用用迭代算法求解,第i步的迭代方程如下

采用FBM求解方程(8a),將各子矩陣分解為上、下和對角矩陣,分別用U、D和L表示。將未知向量分解為前后向分量,方程(8a)中前向電流迭代公式可寫為

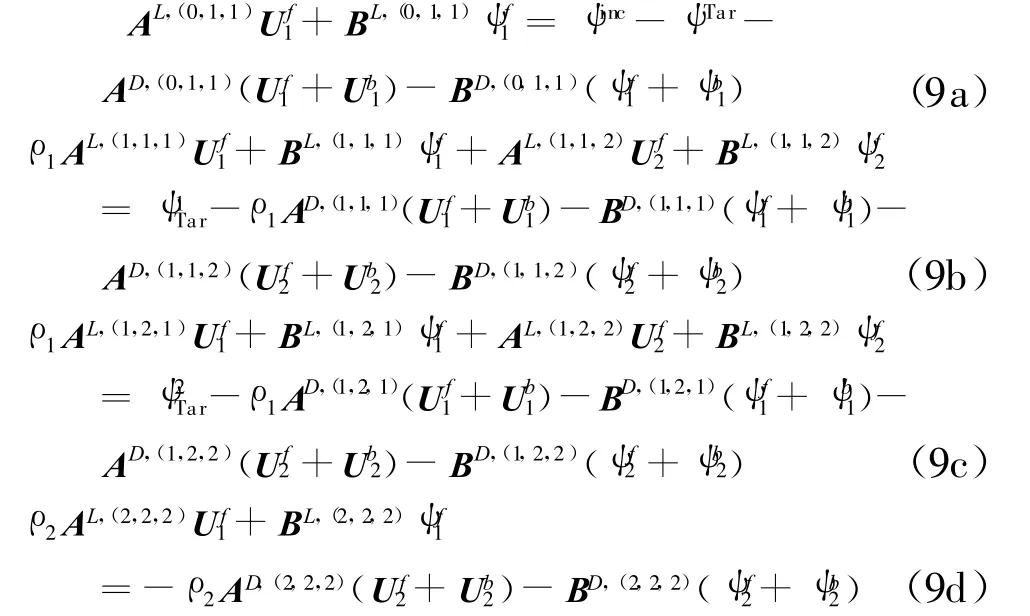
用雙共軛梯度法(Bi-CG)解方程(8b),FBM和Bi-CG求解分別是循環迭代過程,稱為內循環,設其各自的收斂條件為誤差γ=10-4。而方程(8a)和(8b)的互耦迭代過程稱為外循環,定義第i步外循環迭代誤差

3.數值結果的驗證和討論

為了盡量減少數值計算中粗糙面的人為截斷所引起的邊緣效應,一般選取具有一定寬度的錐形波代替平面波入射,本文采用Thorsos錐形波[17],即表達式為

圖2給出了外循環迭代誤差τ(i)隨外循環迭代步數的變化關系。由圖2可知,不論是 TE波還是TM波入射,在經過15步迭代之后,誤差都達到10-7,遠遠滿足精度要求,同時可以看出,TM 波收斂速度更快,但精度有所降低,從圖2還可以看出,在經過4步迭代之后,迭代誤差已經達到10-3,因此,該算法的收斂速度是非常快的。

圖3給出了內循環FBM的迭代步數隨外循環迭代步數的變化關系,由圖可知,經過6步外循環迭代之后,FBM只需一次迭代即可,這與文獻[4]中計算單層粗糙面和上方金屬目標的情況相似。由于FBM在整個計算過程中耗時最多,因此FBM迭代步數的減少大大提高了計算效率。

圖4是實現一次的雙站散射系數,并與傳統矩量法結果進行了比較,圖4(a)是TE波入射結果,圖4(b)是TM波入射結果。由圖可見,兩種方法的結果是相當吻合的,從而驗證了該方法的正確性。本文計算結果是在主頻為1.65 GHz,內存為1 GB的單機上實現的。TE波入射時,用互耦迭代算法實現一次需要145秒,而用傳統矩量法需要298秒,節省了約一半時間,當粗糙面較長時這種優勢更為明顯,體現了該算法在計算速度上的優越性。

圖4 本文算法與傳統矩量法結果對比

其他參數不變,圓柱半徑取 2.5λ,與半徑為2.0λ的結果進行比較。圖5是實現50次得到的雙站散射系數,圖中還給出了只有分層粗糙面時的散射系數。由圖可知,隨著圓柱目標半徑增大,目標與上下層粗糙面的相互作用增強,其對分層粗糙面的散射特性影響越明顯,雙站散射系數越大,垂直極化波入射時散射系數對目標尺寸的變化更敏感。

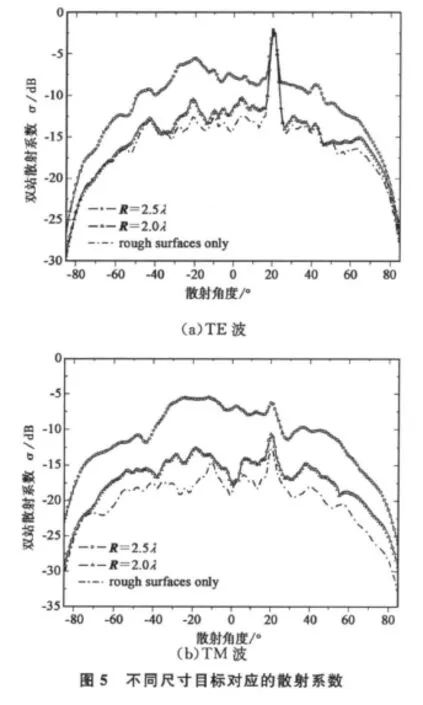
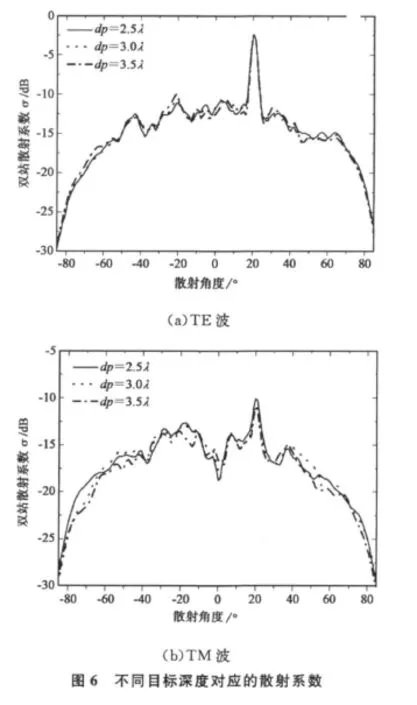
取介質目標深度分別為2.5λ和3.5λ,其他參數固定,相應的雙站散射系數見圖6。由圖可見,隨著目標深度的增加,散射系數有所變化但不是很明顯,這與文獻[8]中的結論是一致的。這是因為目標位于兩層分界面中間,隨著目標深度的增加,目標與上層粗糙面距離增大,而與下層粗糙面距離減小,因此目標與上層粗糙面的相互耦合作用減弱,同時又與下層粗糙面的相互耦合作用增強,因此總體上講,散射系數不會因為目標深度的變化明顯增大或減小。同時可以發現,與圖5類似,垂直極化波入射時雙站散射系數變化更為明顯。

4.結 論

提出了一種基于FBM和Bi-CG的互耦迭代算法(CCIA),并將該方法用于快速計算一維分層粗糙面與下方介質目標的復合電磁散射特性。計算了無限長介質圓柱目標位于雙層粗糙面之間時的雙站散射系數,與用傳統矩量法所得的結果相吻合,驗證了該方法的正確性。對不同極化入射波該算法都具有良好的收斂性,最后討論了目標尺寸和深度變化對散射系數的影響,結果表明,隨著尺寸增大,目標與分層粗糙面的相互作用越強,雙站散射系數變化越明顯,而目標深度的變化對散射系數的影響不明顯。介質目標的存在明顯改變了分層粗糙面的散射特性,當計算分層粗糙面與目標的復合散射場時必需考慮兩者的相互作用。

[1]JOHNSON J T.A study of the four-path model for scattering form an object above a half-space[J].Microwave Optical Technology letters,2001,30(2)：130-134.

[2]JIN Y Q,LI Z.Simulation of scattering form complex rough surface at low grazing angle GFBM/SAA method[J].IEEE Trans.Of Fundamentals and Materials Society(A),2001,121(10)：917-921.

[3]WANG X,WANG C F,GAN Y B,et al.Electromagnetic scattering from a circular target above or below rough surface[C]//Progress In Electromagnetics Research,2003,40：207-227.

[4]YE Hongxia,JIN Yaqiu.Fast iterative approach to difference scattering from the target above a rough surface[J].IEEE T rans Geoscience Remote Sensing,2006,44(1)：108-115.

[5]葉紅霞,金亞秋.三維隨機粗糙面上導體目標散射的解析-數值混合算法[J].物理學報,2008,57(2)：839-846.YE Hongxia,JIN Yaqiu.A hybrid analytical-numerical algorithm for scattering froma 3-D target above a randomly rough surfac[J].Acta Physica Sinica,2008,57(2)：839-846.(in Chinese)

[6]王運華,張彥敏,郭立新.平面上方二維介質目標對高斯波束的電磁散射研究[J].物理學報,2008,57(9)：5529-5536.WANG Yunhua,ZHANG Yanmin,GUO Lixin.Investigation of the scattered field form a two-dimensional dielectric target above the planar surface with a Guass beam incidence[J].Acta Physica Sinica,2008,57(9)：5529-5536.(in Chinese)

[7]王 蕊,郭立新,秦三團,等.粗糙海面及其上方導體目標復合電磁散射的混合算法研究[J].物理學報,2008,57(6)：3473-3480.WANG Rui,GUO Lixin,QIN Santuan,et al.Hybrid method for investigation of electromagnetic scattering interaction between the conducting target and rough sea surface[J].Acta Physica Sinica,2008,57(6)：3473-3480.(in Chinese)

[8]KUO C H,MOGHADDAM M.Electromagnetic scattering from a buried cylinder in layered media with rough interfaces[J].IEEE Trans on antennas and propagation,2006.54(8)：2392-2401.

[9]EL-SHENAWEE M.Polarimetric scatteringfrom two-layered two dimensional random rough surfaces with and without buried objects[J].IEEE Trans Geoscience Remote Sensing,2004.42(1)：67-76

[10]CHEW W C,JIN J M,MICHIELSSEN E,et al.Fast And Efficient Algorithms In Computational E-lectromagnet-Ics,[M].Norwood：Artech House Publishers,2001.

[11]LI J,GUO L X.ZENG H.FDTD Investigation on E-lectro-magnetic Scattering form the PEC Cylinder above Two_Layered Rough Surfaces[C].2008 ICMMT,531-534.

[12]葉紅霞,金亞秋.三維介質粗糙面上導體目標散射的解析-數值混合算法[J].電波科學學報,2008,23(6)：1144-1154 YE Hongxia,JIN Yaqiu.A hybrid analytical-numerical algorithm for computation of scattering from a 3D PEC target above a dielectric rough surface[J].Chinese Journal of Radio Science.2008,23(6)：1144-1154.(in Chinese)

[13]姬偉杰,童創明,閆沛文.粗糙面下方金屬目標復合電磁散射的快速算法[J].電波科學學報,2009,24(5)：939-943.JI Weijie,TONG Chuangming,YAN Penwen.Fast calculation of EM scattering from randomly rough surface with buried PEC target[J].Chinese Journal of Radio Science.2009,24(5)：939-943.(in Chinese)

[14]HOLLIDAY D,DERAAD L L,ST-CYR G J.Forward backward：A new method for computing lowgrazing angle scattering,[J].IEEE Transactions on Antennas Propagation,1996,44：722-729.

[15]CHRISTOPHER D M,TOMASZ M G,HSIU C H,et al.Forward-Backward Method With Spectral Acceleration for Scattering From Layered Rough Surfaces,[J].2006 IEEE T rans antennas propagation,2006,54(3)：1006-1016.

[16]DéCHAM PS N,BEAUCOUDREY N De,BOURLIER C and TOUTAIN S.Fast numevical method for electromagnetic scatfering by rongh layered interfaces：Propagation-imside-layerexpansion method[J].Opt.Soc.Am.A.,2006,23(2)：359-369.

[17]THORSOS E I.The validity of the Kirchhoff approximation forrough surface scatteringusinga Guassian roughness spectrum.[J].Journal of the A-coustical Society of America,1988,83(1)：78-92.

[18]閆沛文,童創明.基于 FGMRES-PBTG算法的介質粗糙面散射特性的模擬[J].電波科學學報,2009,24(1)：115-119.YAN Peiwen,TONG Chuangming.Simulations of scattering characteristic of lossy dielectric surfaces based on FGM RES-PBTG method[J].Chinese Journal of Radio Science,2009,24(1)：115-119.(in Chinese)