基于FDTD的羅蘭-C信號地波傳播特性的時域分析

席曉莉 周麗麗 余寧梅

(西安理工大學(xué)自動化與信息工程學(xué)院,陜西西安710048)

1.引 言

隨著GPS信號電平低,易受到目的性和非目的性干擾等缺點的日益暴露,采用羅蘭-C對其進行有效備份已逐漸成為各國共識[1-2]。許多國際組織、研究群體、制造商目前正積極致力于對羅蘭-C系統(tǒng)的現(xiàn)代化改造以及功能擴展[1-3]。

地波信號在傳播過程中受到傳播路徑的大地電參數(shù)、地形起伏及大氣折射指數(shù)等因素的影響,難以精確預(yù)測,從而降低羅蘭-C系統(tǒng)的絕對定位精度,因此對低頻地波特性,特別是對沿不規(guī)則地面?zhèn)鞑サ奶匦缘木_預(yù)測尤為重要。

目前對羅蘭-C信號地波傳播特性求解的主要方法有基于均勻光滑球地面的Fock繞射法,基于分段不均勻光滑球地面的Millington經(jīng)驗公式、Wait積分法、波模轉(zhuǎn)換法、拋物線方程方法[4]以及基于不均勻不光滑地面的積分方程方法等[5-6],這些方法均是依據(jù)傳播路徑的電導(dǎo)率和地形數(shù)據(jù)對100 kHz單頻信號的地波場強、二次時延進行預(yù)測的。但實際羅蘭-C信號為100 kHz載波調(diào)制的高斯脈沖,接收機測量的信號到達時刻為某一固定載波周期的過零點,因此在復(fù)雜的傳播路徑上,周圍環(huán)境對羅蘭-C時域脈沖信號測量結(jié)果的影響會和單頻信號的穩(wěn)態(tài)預(yù)測結(jié)果存在較大誤差;另外脈沖信號在有耗媒質(zhì)表面?zhèn)鞑ゴ嬖诘纳⑿?yīng)也會使單頻信號的預(yù)測精度與實際信號存在一定差異。本文擬采用時域數(shù)值計算的方法針對該問題展開研究。

FDTD是最常使用的電磁場時域數(shù)值計算方法,近年已逐漸用于低頻段和甚低頻段沿地球表面電波傳播領(lǐng)域的研究[7-9],但多是考慮地-電離層腔體傳播效應(yīng)[7-8]。文獻[9]對FDTD算法及各種經(jīng)典算法在低頻地波傳播預(yù)測中的性能進行了比較,但均是在頻域進行的討論,未分析信號的時域特性。文章采用FDTD算法仿真了實際羅蘭-C信號在均勻光滑平地面、分段不均勻光滑地面以及含有高斯形山脈不規(guī)則地面上的地波傳播場強和二次時延,并和100 kHz時諧源的結(jié)果進行了比較,旨在分析100 kHz單頻近似結(jié)果的誤差及其適用范圍。

2.基本理論

2.1 羅蘭-C信號波形

羅蘭-C信號的脈沖波形是以發(fā)射天線底部的電流波形定義的,正相位編碼的羅蘭-C發(fā)射信號電流波形前沿定義如下[10]

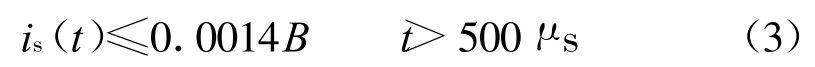
B是公式(2)所表示的信號包絡(luò)的最大值：

實際羅蘭-C信號場強波形如圖1所示。

圖1 羅蘭-C信號場強波形

2.2 羅蘭-C信號的到達時刻

羅蘭-C信號以多脈沖的脈沖組形式發(fā)射,副臺每個脈沖組含8個脈沖,相互間隔1 ms;主臺每個脈沖組含9個脈沖,前8個脈沖相互間隔1 ms,第9個脈沖距第8脈沖2 ms,用以標識主臺。脈沖組信號到達時刻是指脈沖組第1個脈沖第3載波周期正向過零點時刻(如圖1所示),第三個脈沖負峰值為信號采樣點脈沖強度[10]。

傳統(tǒng)的羅蘭-C接收機是通過測量主副臺脈沖組信號到達時間差進行雙曲線定位;經(jīng)數(shù)字化改造后的現(xiàn)代羅蘭-C接收機,其發(fā)射信號編碼中包含信號的發(fā)射時刻信息,可直接從測量信號的到達時刻獲取傳播時延,用于授時和定位。對傳播時延進行二次時延修正,可有效提高定位和授時精度。

2.3 羅蘭-C信號二次時延及場強

經(jīng)典的低頻地波傳播理論中,收發(fā)點的傳播時延表示為

對于包周差為0的標準包絡(luò),若發(fā)射天線效率為1,信號包絡(luò)峰值場強為

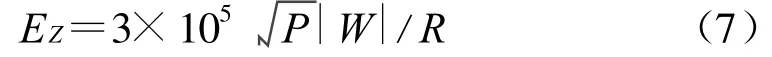
3.數(shù)值算法及模型

3.1 二維柱坐標FDTD

當(dāng)激勵源是理想垂直電偶極子,并假設(shè)地形沿φ方向一致時,此時低頻地波傳播問題可用二維柱坐標FDTD方法求解。設(shè)激勵源位于ρ=0的軸上,離地高度z=h,σ是大地電導(dǎo)率是大地相對介電常數(shù)。

二維柱坐標麥克斯韋方程組在擴展柱坐標系下表達式為[11]

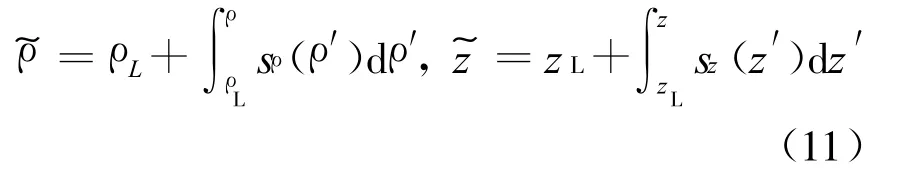
方程(12)和(13)差分格式如下

3.2 數(shù)值計算模型

文中FDTD計算區(qū)域在ρ方向取100 km,z方向取5.625 km(源點地表以下取0.75 km)。采用均勻剖分方式,空間和時間步長分別取18.75 m,31.25 ns。計算模型網(wǎng)格總大小為×300,計算區(qū)域的上側(cè)和右側(cè)邊界設(shè)置為 10層PML吸收層,左側(cè)為軸對稱邊界。在高出地面一個網(wǎng)格點處加源,天線峰值輻射功率均歸一化到 1 kW。迭代總時間步為12500。在FDTD計算過程中沿傳播路徑每間隔18.75 m提取接收點場強和二次時延。當(dāng)采用100 kHz正弦饋源時,為盡可能得到穩(wěn)態(tài)結(jié)果,在計算的最后周期提取場強和相位,當(dāng)采用羅蘭-C脈沖源時,提取脈沖信號的包絡(luò)峰值和第三周期正向過零點時刻。根據(jù)公式(5),可求得二次時延,其中正弦信號提取的到達時刻還需再扣除提取時刻信號的重復(fù)周期數(shù),另外,二次時延求解中需加上場強載波相位與發(fā)射天線電流載波相位之間存在的2.5 μ s相移[10]。

4.數(shù)值結(jié)果

4.1 均勻傳播路徑結(jié)果比較

采用FDTD算法,分別計算兩種源(100 kHz正弦和羅蘭-C時域信號)在不同電參數(shù)的均勻光滑平地面?zhèn)鞑r的場強與二次時延,其結(jié)果與解析結(jié)果間的誤差見圖2。地層電參數(shù)取四組

從圖2可以看出：(1)100 kHz正弦信號和羅蘭-C信號的FDTD計算的場強誤差分布規(guī)律基本相同,海水路徑(σ=5 S/m)基本沒誤差,其他路徑誤差隨電導(dǎo)率和介電常數(shù)的減小而減小,且均隨傳播距離的增加而增加,該誤差主要由于FDTD數(shù)值色散引起。(2)FDTD計算的100 kHz正弦信號的時延誤差基本在FDTD的一個時間步長范圍內(nèi),且隨距離變化較小;羅蘭-C信號的時延誤差隨傳播距離的增加而增大,隨電導(dǎo)率的增大而減小,該誤差主要是由羅蘭-C信號在有耗介質(zhì)表面的色散造成的。其次羅蘭-C信號與100 kHz信號存在約為100 ns的整體偏差,說明羅蘭-C信號的載波相位與發(fā)射電流載波相位差更接近2.4 μ s而不是2.5 μ s,這與文獻[12]中取值相同。

4.2 分段不均勻傳播路徑結(jié)果比較

圖3是傳播路徑為三段不均勻光滑平地面時采用FDTD計算的兩種不同源所對應(yīng)的結(jié)果比較。各段電參數(shù)分別為各段長度均為30 km。

從圖3可以看出,分段不均勻路徑情況下,兩種源對應(yīng)的場強結(jié)果吻合較好,誤差小于0.12 dB,整個路徑的二次時延誤差小于100 ns。地面媒質(zhì)的電參數(shù)不同,導(dǎo)致羅蘭-C脈沖信號的色散不同,因此在不同電導(dǎo)率的傳播路徑上,兩種源的二次時延差異略有不同。

4.3 不均勻不光滑傳播路徑結(jié)果比較

圖4(a)和(b)是傳播路徑中含有單個不同陡峭程度的高斯形山脈時,兩種不同源所對應(yīng)的結(jié)果比較,山脈的地形函數(shù)形式如下

從圖4(a)可以看出,當(dāng)路徑中山體陡度較小時,兩種源對應(yīng)的場強吻合得很好,二次時延約有接近100 ns的初始偏差。從圖4(b)可以看出,當(dāng)山體比較陡時,山后兩種源結(jié)果仍然吻合得很好,但由于地形變化劇烈,山前場強及二次時延疊加了一個明顯振蕩信號,且離山越近,振蕩越強;單頻信號振蕩范圍較廣,羅蘭-C脈沖信號場強振蕩僅存在于山脈前約3個波長范圍,而二次時延的振蕩范圍只有不到2個波長,這主要源于羅蘭-C為時域信號,其到達時刻和場強提取點為波形中的固定點,因此反射及散射波對其影響范圍有限。

5.結(jié) 論

通過對兩種源在不同傳播路徑下地波傳播特性的計算和比較,可以得出如下結(jié)論：(1)采用頻域100 kHz的饋源得到的低頻地波的傳播時延特性和真實羅蘭-C間的時延存在一個由有耗媒質(zhì)引起的色散誤差,該誤差隨傳波距離的增大而增大;(2)在地形起伏不大的傳播路徑,二者的結(jié)果誤差較小;當(dāng)傳播路徑地形起伏較大時,山前信號由于反/散射信號的疊加出現(xiàn)振蕩,該現(xiàn)象在單頻結(jié)果中被放大,影響范圍沿來波方向一直延伸,而實際羅蘭-C信號的振蕩效應(yīng)僅存在于山前幾個波長范圍內(nèi)。

本文對100 kHz單頻近似真實羅蘭-C信號時的誤差分析對羅蘭-C信號的理論預(yù)測及實驗測量具有一定參考價值。

[1]JOHNSON G,HARTNETT R,SWASZEK P,et al.Can Loran meet GPS backup requirements?[J].IEEE Aerospace and Electronic Systems Magazine,2005,20(2)：3-12

[2]SHERMAN C L,BENJAM IN B P,Per K E,et al.Loran data modulation：extensions and examples[J].IEEE Aerospace and Electronic Systems Magazine,2007,43(2)：628-644.

[3]National Security Space Office(NSSO).National Positioning,Navigation,and Timing Architecture Study,Final Report[R].Washinton DC,2008.

[4]潘威炎,彭懷云,張紅旗.非均勻光滑球面地波衰減因子的拋物方程算法[J].電波科學(xué)學(xué)報,2006,21(1)：37-42.PAN Weiyan,PENG Huaiyun,Zhang Hongqi.Parabolic equation algorithm of wave attenuation along inhomogeneous smooth ground[J].Chinese Journal of Radio Science,2006,21(1)：37-42.(in Chinese)

[5]WAIT J R.The ancient and modern history of EM ground-wave propagation[J].IEEE Antennas and Propagation Magazine,1998,40(5)：7-24.

[6]DeMINCO N.Propagation prediction techniques and antenna modeling(150 to 1705 kHz)for intelligent transportation systems(ITS)broadcast applications[J].IEEE Antennasand Propagation Magazine,2000,42(4)：9-34.

[7]WANG Y,XIA H G,CAO Q S.Analysis of ELF propagation along the earth surface using the FDTD model based on the spherical triangle meshing[C]∥Antennas and Wireless Propagation Letters,IEEE,2009,8：1017-1020.

[8]SIM PSON J J,TAFLOVE A.A review of progress in FDTD Maxwell＇s equations modeling of impulsive subionospheric propagation below 300 kHz[J].IEEE T ransactions on Antennas and Propagation,2007,55(6)：1582-1590.

[9]周麗麗,席曉莉,余寧梅.不規(guī)則地面低頻地波傳播預(yù)測方法的性能比較[J].電波科學(xué)學(xué)報,2009,24(6)：1158-1163.ZHOU Lili,XI Xiaoli,YU Ningmei.Comparison of three methods of calculating low frequency groundwave propagation over irregular terrain[J].Chinese Journal of Radio Science,2009,24(6)：1158-1163.(in Chinese)

[10]邁迪.長河二號工程-遠程無線電導(dǎo)航系統(tǒng)[M].北京：電子工業(yè)出版社,1993：21-30.

[11]TEIXEIRA F L,CHEW W C.Systematic derivation of anisotropic PML absorbing media in cylindrical and spherical coordinates[J].IEEE Microwaveand Guided Wave Letters,1997,11(7)：371-373.

[12]LAST J D,WILLIAMS P,PET ERSON B,et al.Propagation of Loran-C signals in irregular terrainmodelling and measurements part 2：measurements[C]∥29th Annual Convention and Technical Symposium,International Loran Association.Washington DC,USA,2000.