基于方向自適應模板的UMHexagonS算法改進*

趙子武，鄒雪妹，程 飛，魏小文

（上海大學 通信與信息工程學院，上海 200072）

責任編輯:孫 卓

1 引言

在視頻壓縮編碼中，時域冗余主要通過運動估計和運動補償來消除，它也是整個編碼器比較耗時的部分。針對運動估計最先提出的全搜索算法[1]:在參考幀預先定義好的搜索區域中，將當前幀與搜索區域中所有的候選塊進行比較，最小匹配誤差的塊為最優塊。全搜索法（FS）能夠獲得非常高的搜索精度，但運算量十分巨大，之后的運動搜索算法都以在不影響精度的同時減少計算量為目標。 三步搜索法（TSS）、兩維對數法（LOGS）、十字型搜索法（CS）、四步搜索法（FSS）、梯度下降法（BBGDS）[2]、鉆石搜索法（DS）[3]和六邊形搜索法（HEXBS）[4]等的搜索速度比全搜索有了提高，但它們沒有充分考慮時間和空間上相鄰塊的信息，搜索時容易陷入局部最小值，從而導致匹配精度差。之后提出的運動估計算法主要集中于以下幾個方面:充分考慮時間和空間上的相鄰宏塊信息，針對視頻中靜止宏塊較多的情況提出自適應提前終止策略，改變搜索模板，根據初始預測運動矢量自適應修改搜索區域大小等。例如MPEG-4標準第7部分已經采用的MVFAST[5]和改進算法 PMVFAST[6]。

基于上述研究，H.264標準采用了UMHexagonS算法[7]，該算法能同時適應小運動和大運動情況下的運動估計，并能得到與全搜索基本一樣的精度和率失真特性，同時最多能比全搜索節省90%的時間。因此，H.264/AVC標準采納了該運動估計算法。文獻[8]中UMHexagonS算法改變了搜索模板，一定程度上減少了運動估計時間。

2 UMHexagonS算法

非對稱十字型多層次六邊形格點搜索算法（UMH-exagonS）搜索步驟[1]如下:

1）初始搜索點預測。取對應費用函數最小的點為初始搜索點（預測搜索法包括針對空間相關性的中值預測、上層預測、前一幀對應塊預測和鄰近參考幀預測），然后判斷是否提前截止。

2）非對稱十字型搜索。由于一般物體水平方向運動要比垂直方向運動劇烈，所以將垂直方向設置為水平方向搜索范圍的一半，判斷是否提前終止搜索。

3）非均勻多層次六邊形格點搜索分步進行5×5小矩形窗全搜索和擴展的多層次六邊形格點搜索，同時也要判斷是否提前終止搜索。

4）采用擴展多層次六邊形格點搜索和小菱形搜索模式循環進行搜索，持續搜索到最小費用函數值的點位于菱形搜索窗口的中心點為止。

該算法充分考慮了空間和時間的相關性以及H.264采用的宏塊劃分技術中不同尺寸塊的運動矢量相關性，進行初始點預測，針對運動幅度的大小采用自適應的六邊形格點搜索和菱形搜索，具有很強的內容適應性，同時應用提前終止策略避免了不必要的運算，這些都取得了很好的效果。

3 改進UMHexagonS算法

要保證同樣的編碼效果，同時進一步減小UMHexagonS算法的運算量，筆者提出了改進方法，主要使初始運動矢量更準確，減少5×5全搜索點數，通過精確的運動矢量確定搜索方向并改用擴展的梯形格點進行搜索。

3.1 初始運動矢量改進

在原算法4種初始搜索點預測模式基礎上提出第5種預測模式:當前塊的左、上、右上塊的運動矢量分別為 MV1，MV2，MV3，參考幀同位置塊的運動矢量為 MV′1，MV′2，MV′3。

1）中值預測 。 PMV1=mediam（MV1，MV2，MV3），PMV2=mediam（MV′1，MV′2，MV′3），取兩者中的最小SAD作為初始MV。

2）PMV=mediam（MV1，MV2，MV3，MV′1，MV′2，MV′3）。

3）Weighted 預測。PMV1=0.375（MV1+MV2）+0.25MV3，PMV2=0.375（MV′1+MV′2）+0.25MV′3，取兩者中的最小SAD做為初始MV。

對上述3種方法進行實驗測試證明第3種方法比較好，則本算法采用Weighted預測。

3.2 5×5全搜索改進

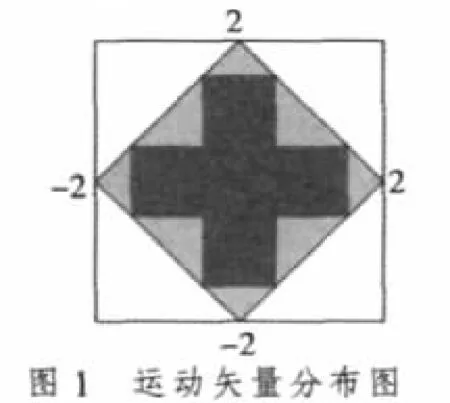
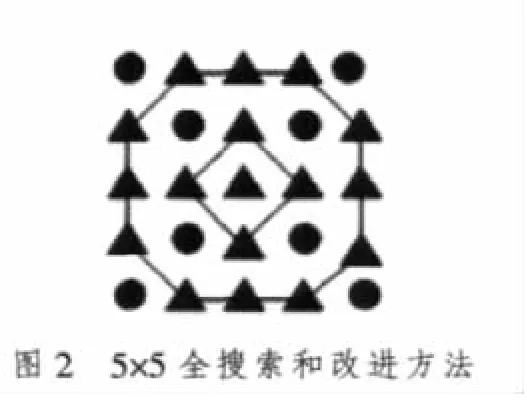
5×5模式因為采用了全搜索模式，所以需要計算25個搜索點，運算量相對較大。在文獻[8]中，筆者對常用視頻序列的運動矢量做了詳細的統計分析，發現運動矢量大部分落于[-2，2]區域中，且以不同比例集中分布在中心附近的特定區域內。如圖1所示，有大約81.8%的運動矢量分布在中心附近范圍±2的正方形區域內（25個點），大約77.52%的運動矢量分布在中心附近范圍±2的菱形區域內（13個點），大約74.76%的運動矢量集中分布在中心附近范圍±2的十字形區域內（9個點），而且匹配點在中心點的概率最高，其次為中心點上、下、左、右4個點，而在周圍右上、左上、右下、左下對角點概率相對較小。本算法參考以上研究結果，在基本保持搜索精度的情況下，通過采用六邊形、八邊形或大小菱形相結合等方法進行比較實驗測試后共采用17個點（如圖2中的小三角形）代替5×5全搜索（如圖2中的小三角形和小圓點）模式25個點，減少了32%的運算量。

3.3 六邊形格點搜索改進

首先根據3.1節中得到的最優初始運動矢量（MVx，MVy）計算 MvRatio=MVx/MVy，根據 MvRatio判斷運動矢量所在的區域，采用可變搜索模板進行搜索從而減少搜索點。 比如（MVx，MVy）=（1，2），則 MvRatio=0.5，用不斷擴大搜索模板搜索第 1，2 象限；（MVx，MVy）=（-2，1），則用不斷擴大的搜索模板搜索第2，3象限。在進行搜索模板的選擇時，對半六邊形、三角形、梯形和矩形等模板進行實驗測試，在考慮搜索精度和時間的情況下，最終選擇梯形模板。非對稱六邊形要搜索16個點，而本算法的梯形只需搜索7個點，在保證搜索質量的同時能減少56.25%的運算量。圖3為改進UMHexagonS算法的搜索步驟。

4 實驗結果與分析

為了驗證改進UMHexagonS算法的有效性，采用JVT參考軟件JM8.6進行仿真實驗。實驗采用不同運動類型的標準視頻序列bus_cif，mobile_cif，flower_cif，stefan_cif，foreman_cif，coastguard_cif等作為測試序列。表1是本實驗采用的JM代碼的編碼控制參數。

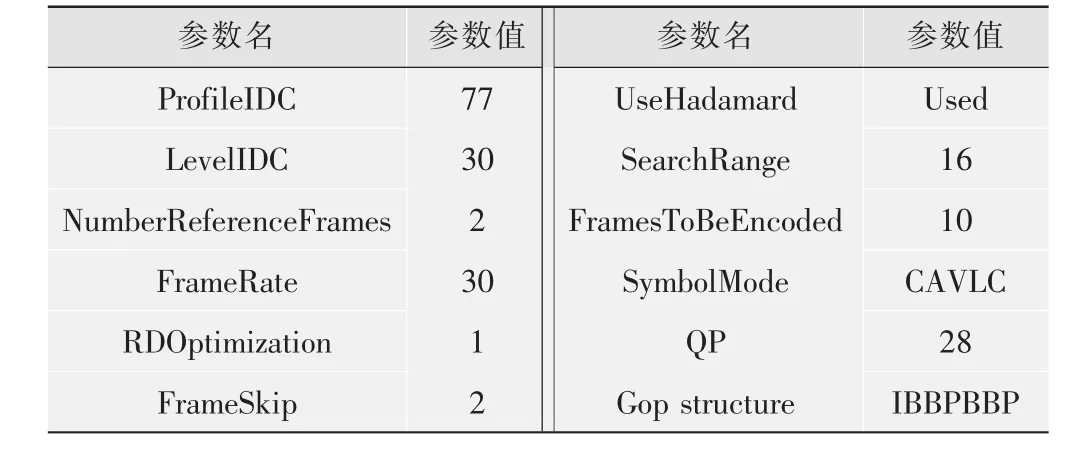
表1 JM編碼控制參數

本實驗分別采用標準算法和改進算法對不同視頻序列的前28幀進行編碼。表2給出了兩種方法的運動估計總耗時并進行比較，表3給出了兩種算法的亮度平均峰值信噪比。從兩表中可以看出，采用改進算法的PSNR基本不變，在保持圖像質量的同時有效降低了運動估計時間，對運動很緩慢的序列效果提高不大，但對劇烈運動序列效果很明顯。表4給出了兩種算法的平均比特率的比較，可以看出改進算法經過視頻編碼后的比特數有極其微小的增加。綜上所述，改進算法在降低運動估計時間的同時非常好地保持了原算法的率失真性能，碼率基本不變，對圖像質量沒有影響。

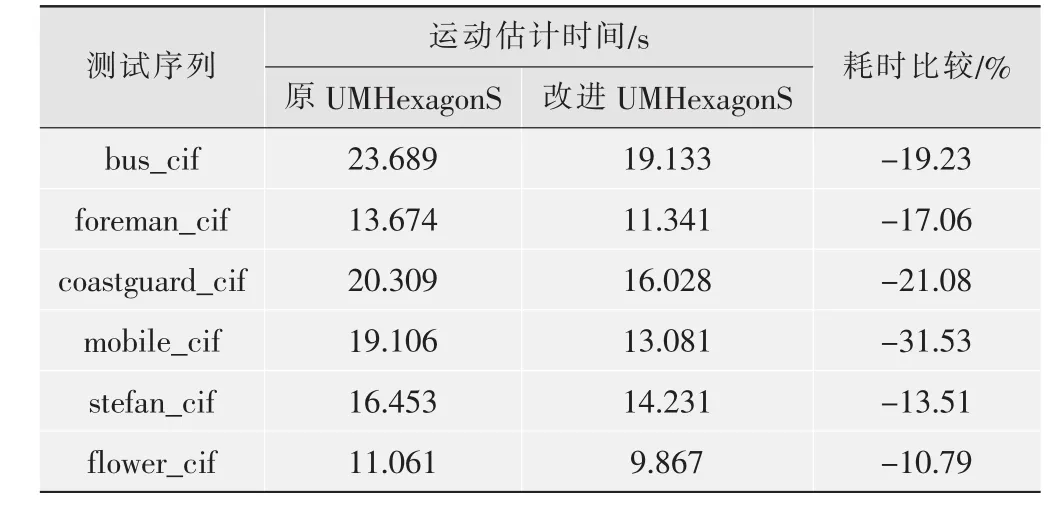
表2 視頻編碼耗時和運動估計耗時

表3 視頻亮度分量的平均峰值信噪比

表4 視頻編碼平均比特率

5 小結

筆者對運動估計經典算法和H.264采用的UMHexagonS算法進行了簡單的分析，并提出了一種改進算法。該算法同時考慮了視頻序列的時域和空域的相關性，使初始運動矢量預測更準確，減少5×5全搜索中的相對不重要搜索點和運算量，根據初始運動矢量的方向使用可變方向的梯形模型搜索，加快搜索速度。在不影響搜索精度，碼率基本不變的情況下大幅減少運動估計的運算量，取得了很好的效果。

[1]畢厚杰.新一代視頻壓縮編碼標準——H.264/AVC[M].北京:人民郵電出版社，2005.

[2]LIU L K，FEIG E.A block-based gradient descent search algorithm for block motion estimation in video coding[J].IEEE Trans.Circuits and Systems for Video Technology，1996，6（4）:419-422.

[3]ZHU S，MA K K.A new diamond search algorithm for fast blockmatching motion estimation[J].IEEE Trans.Image Processing，2000，9（2）:287-290.

[4]ZHU C， LIN X， CHAU L.Enhanced hexagonal search for fast block motion estimation[J].IEEE Trans.Circuits and Systems for Video Technology， 2004，14（10）:1210-1214.

[5]ISO/IEC JEC1/SC29/WG11 M5453，Report on performance of fast motion estimation using motion vector field adaptive search techni-que（MVFAST）[S].1999.

[6]TOURAPIS A M，AU O C，LIOU M L.Predictive motion vector field adaptive search technique-enhancing block based motion estimation[EB/OL].[2009-11-09].http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.17.9457&rep=rep1&type=pdf.

[7]CHEN Z B， XU J F， HE Y， et al.Fast integerpel and fractionalpel motion estimation for H.264/AVC[EB/OL].[2009-11-09].http://linkinghub.elsevier.com/retrieve/pii/S1047320305000787.

[8]段青青，宋瑞.一種H.264/AVC中的快速運動估計算法[J].計算機工程，2008，34（16）:244-246.