小波分析在故障診斷中的應用

湯石雄

（海軍榆林保障基地，榆林 572021）

1 引 言

在對設備或系統的故障診斷過程中，突變信號往往對應著某些特定的故障狀態。一般來說，系統正常運行時的特征信號都比較平穩，而一旦出現故障，往往會產生具有奇異性的突變信號。例如系統在運行過程中產生的撞擊、震蕩、摩擦、轉速突變、結構變形和斷裂等都可以反映在信號的突變點中，信號突變點的奇異性檢測可以有效地揭示故障信息。因此，檢測、分析并識別系統中的各種信號，并判斷其狀態，是對設備進行故障診斷的有效方法。小波分析從數學上講可以認為是一個分析波形的時頻放大鏡，它能將波形上的某一段取出來進行專門的時域和頻域分析，因此，可以找出信號的具體特征，從而進行信號的識別、變換等工作。

小波變換的模極大值對應于信號的奇異點，可通過檢測模極大值來尋找信號的奇異點，進而進行故障診斷[1-4]。

2 信號的小波變換理論

定義 1[4,5]：令 Ψ(t)∈L2(R)，且?( 0)∈0，則由生成的函數族{Ψa,b(t)}稱連續時間小波，或稱分析小波。其中{Ψ(t)}稱為母小波或基本小波，a稱為尺度參數或伸縮參數，b稱為平移參數。稱為小波的允許條件。

定義2：函數f(t)∈L2(R)的連續小波變換，定義為：

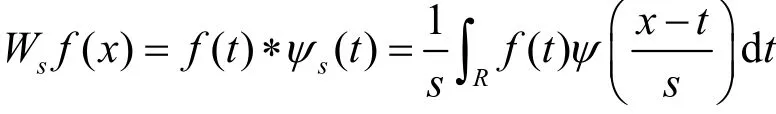
小波變換具有“恒Q特性”和“變焦距特性”，可以對時域和頻域進行局部定位，并能檢測信號及其微商的突變，被稱譽為“數學顯微鏡”，在信號處理、圖像處理、模式識別、故障診斷等領域應用廣泛。

2.1 小波降噪應用分析

在對設備進行故障診斷時，如果不對采集的信號進行有效地降噪，實現信噪分離，那么后續的數據處理和特征提取將產生很大的誤差，從而影響故障診斷的精度。傳統的信號降噪一般采用傅里葉變換的方法，通過傅里葉變換（FFT）實現信號降噪是通過對原信號在一定范圍內濾波來抑制噪聲的頻譜，具體過程是：首先，對原信號進行傅里葉變換求出其頻譜；然后，根據頻譜對不需要的頻譜成分進行濾波，抑制噪聲信號的頻譜；最后，對濾波后的頻譜進行傅里葉逆變換，得到降噪后的信號。

傅里葉變換的一個嚴重缺陷是不能表達時域信息，對系數的處理方法相對單一。因此，傅里葉變換在實際應用中存在很大局限性，主要表現在頻譜混疊、頻譜泄露和柵欄效應，一般僅適合于平穩、緩變信號的頻譜分析。后來的短時傅里葉變換雖然可以表達時域信息，但在相空間中的分辨率是固定的，不能反映信號的瞬時特點。小波變換從原理上克服了傅里葉變換的缺陷。首先，小波分析是按照頻帶而不是頻點的方式處理頻域信息，而利用對信號的時域加窗，取消了其整周期采樣的限制，而其頻域緊支性保證了帶通濾波性質，因此，當信號頻率微小波動以及包含非正次諧波時，不會出現傅里葉分析中的頻譜泄露和頻譜波動現象；其次，小波變換能根據信號頻率的高低，通過尺度伸縮得到可調的時頻窗，這使其具備很強的奇異、突變信號識別能力，能有效地檢測和定位信號中混有的高頻干擾成分并加以分離。小波分析可通過在分解之后的各個層次上選擇閾值對噪聲成分進行抑制，充分發揮了時域分析和頻域分析各自的優點，提供了更為靈活的信號分析和處理方法。

利用小波變換降噪的原理是，小波變換對確定信號有一種“集中”的能力，可以使一個信號的能量在小波變換域集中于少數系數上，而高斯白噪聲的小波變換仍是同一幅度的高斯白噪聲，一般而言，信號的小波系數值大于那些能量分散于大量小波系數上且幅值較小的噪聲的小波系數值。因此，可以通過小波變換將噪聲從信號中分離出來。

小波分析用于降噪的基本過程是：首先，通過選定一種小波，對信號進行N層小波分解；然后，對分解得到的各層系數進行閾值處理；最后，降噪處理后的小波系數通過小波重建恢復原信號。在正交小波中，正交基的選取比傳統方法更接近實際信號本身，所以通過小波變換可以更容易地分離出噪聲和其他不需要的信息[5,6]。

2.2 間斷點檢測應用分析

故障特征提取是故障診斷最重要也是最困難的問題。一般來說，系統的故障最初較微弱，其特征淹沒在背景信號中，傳統的信號處理方法難以分離，使其不能被及時發現和排除，最終演變為嚴重故障，影響系統運行。工程實踐表明：對于某一特定的系統，在正常狀態下，有特定的特征波形。對于以信號展開或變換理論為基礎的特征提取方法，一個重要問題是基函數的選取要與被提取的特征相匹配。小波理論提供了不同特性的、豐富的基函數，使得對某一個特定的問題可以選擇合適的基函數以獲得較好的故障分類信息。

小波變換實質上是在每一個變換尺度上進行一系列相關運算，當信號特征與小波特性相似時，就會出現較大的小波系數，因此，采用與故障特征匹配的小波基函數分析系統的動態信號，可以顯示被淹沒的故障信號，在信號發生突變時，其小波變換后的系數具有模極大值，因此，可以通過檢測小波系數的模極大值來檢測突變信號的奇異點，進而得到系統的故障信息。例如，旋轉機械的振動表現為以轉速為周期的周期性振動。當旋轉機械存在轉子質量不平衡、軸系不對中等故障時，在每個旋轉周期都將產生較強的振動現象，并在振動信號中出現不同類型的奇異點，這些奇異點通常包含有益的故障信息。

在數學上采用 Lipschitz指數來描述某一點的奇異性。

定義3[5,7]：設n是一非負整數，n＜α≤n+1，f( t )在 t0處具有Lipschitz 指數α，當且僅當存在常數A和h0＞0及 n 階多項式pn(t)，使得對于任何 h≤h0均有

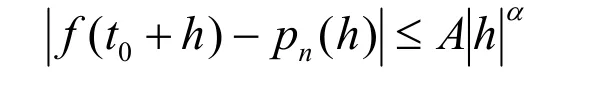
成立。Lipschitz 指數越大，則函數越光滑。如果f ( t )在 t0的Lipschitz 指數小于1，則稱t0是f ( t )的奇異點。信號的奇異點可以從小波變換的模極大值檢測出來。信號的突變越大，其小波變換的模極大值就越大，而信號的突變點就是可能的故障點。因此，可以通過對小波變換模極大值的檢測來判斷信號中是否存在奇異點，進而達到故障檢測的目的。

在實際信號處理中，低頻信號一般持續時間長，因此總是希望時窗盡量寬些，而頻窗盡量精細些；分析高頻信號時，則希望時窗窄些，頻域可以適當降低精度。小波變換具有自適應的時頻窗，在低頻區時窗寬而頻窗窄，在高頻區時窗窄而頻窗寬，這與需要處理的信號的特性完全符合。一般情況下，短支集小波在處理間斷問題時比長支集小波更有效。根據實踐經驗發現，在選擇小波過程中，如果處理的信號本身是間斷的，可以使用haar小波；而如果處理的信號的第i階導數是間斷的，則應使用消失矩為i的小波。

3 實例研究

對于一個頻率突變的信號，應用小波變換可以將信號突變的時間點和位置檢測出來。例如，對一個頻率突變的信號利用db5小波對原信號進行5層分解，信號的波形及小波分解系數如圖1所示。其中s為原信號，a1-a5為近似系數，d1-d5為細節系數[6]。

從小波分解圖上可以看出，第一層和第二層細節系數清楚地反映出了信號在500附近頻率的不連續性。這兩組系數中間都只有一個很窄的區域包含絕對值很大的系數，這表明原信號在該點附近有間斷。可見，小波分析不僅能清晰地反映出信號的間斷，而且能準確定位間斷點的位置。從圖中可以看出，d1已經包含了間斷點的信息，而高頻信號從d2才開始出現，說明間斷點的頻率比信號高頻部分的頻率還要高。

對同一信號進行傅里葉變換，結果如圖2所示。從傅里葉變換結果可以看出，在偽頻率分別為5和50處出現兩個強度相當的頻率成分，這和小波分析的結果類似，但傅里葉變換不能得到間斷點的位置。因此，小波變換在處理多頻率、含間斷點的信號時，比傅里葉變換具有更大的優勢。因此，在故障診斷領域應用廣泛。傅里葉變換由于只反映頻域的特性，因此，只能是孤立的幾根譜線，而小波變換基于時頻的聯合分析，可以對信號的時頻特性進行精確分析和定位。

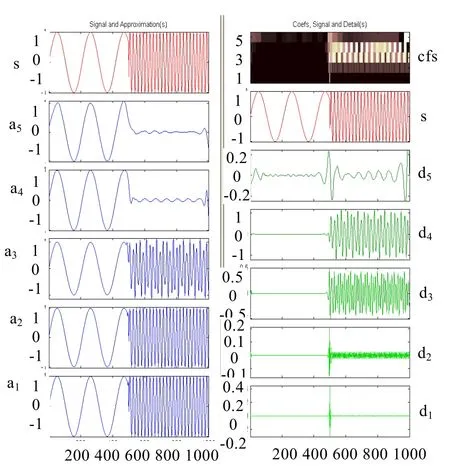
圖1 頻率突變信號的小波變換

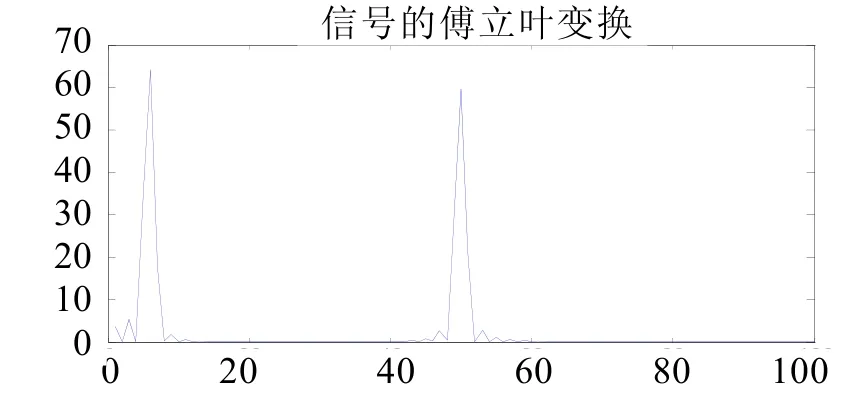
圖2 頻率突變信號的傅里葉變換

4 結束語

本文通過理論分析和實例驗證，給出了應用小波分析進行故障診斷的方法，通過與傅里葉變換的分析、對比可以看到，小波分析在信號降噪和奇異點的檢測方面有FFT所無可比擬的優勢。當然，小波分析的應用領域遠不止這些，同時，小波變換只對低通濾波器的輸出進行遞歸分解，即只對信號的低頻空間進行進一步的分解，因此，存在高頻段頻率分辨率差，低頻段時間分辨率差的問題。針對這個問題，引入了小波包分析理論。總之，小波變換為信號處理技術提供了強大的工具，并處在不斷發展完善過程中，應用前景廣闊。

：

[1]牛星巖, 沈頌華. 基于小波變換的整流裝置故障特征提取[J]. 電子測量技術, 2007(10): 122-126.

[2]陳果. 基于小波分析的轉子故障信號自適應降噪技術[J]. 航空動力學報, 2008(1): 9-16.

[3]周小勇, 葉銀忠. 小波分析在故障診斷中的應用[J].控制工程, 2006(1): 70-73.

[4]崔寶珍, 王澤兵, 潘宏俠. 小波分析-模糊聚類法用于滾動軸承故障診斷[J]. 振動、測試與診斷, 2008(2):151-154.

[5]吳正國, 尹為民, 侯新國等. 高等數字信號處理[M].北京: 機械工業出版社, 2009.

[6]高成主編. Matlab小波分析與應用（第二版）[M].北京: 國防工業出版社, 2007.

[7]胡志坤, 桂衛華, 何多昌等. 電力電子電路故障的小波分形檢測方法[J]. 控制工程, 2008, 15（3）:337-341.