數字圖像的逆濾波復原

陳華玲，馮 桂，寥家亮

（華僑大學 信息科學與工程學院，福建 泉州 362021）

1 引言

在各類圖像系統中，由于圖像的傳送和轉換，如成像、復制、掃描、傳輸、顯示等，總要造成圖像的降質[1]，典型表現為圖像模糊、失真、有噪聲等，這一過程稱為圖像的退化。相反的，將圖像退化的過程模型化，并據此采取相反的過程以求得原始（清晰）圖像即為圖像復原技術。圖像復原的質量和可靠性通常依賴于對圖像退化信息了解的確切程度。所以模糊圖像復原一般分為兩個步驟：一是通過系統辨識方法求解退化函數（PSF），二是采取相應算法由退化圖像和退化函數復原出原始圖像。

系統辨識方法通常有測試靶方法、互相關方法和圖像辨識系統方法[2]。前兩種方法適用于手頭有一套攝像系統，對系統輸入的一些特殊信號得到輸出，然后根據輸入和輸出計算系統傳遞函數，即PSF。后一種方法則試圖根據退化圖像本身來確定退化的PSF。筆者從離焦模糊和運動模糊產生的原因出發，結合模糊圖像與頻譜圖的對應關系，應用Hough變換估計出退化參數，然后利用逆濾波方法對模糊圖像進行復原。

2 逆濾波復原原理

原始圖像 f（x，y）經過一個算子或者系統 h（x，y）作用后，與噪聲 n（x，y）疊加而形成觀察到的退化圖像 g（x，y）[3]。其數學表達式為

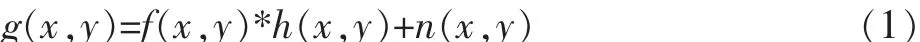
式中：h（x，y）是一個綜合了所有退化因素的函數。式（1）對應的頻域表達式為

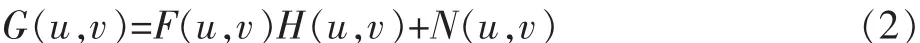
由式（2）可以得到

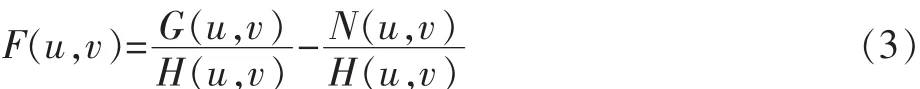
將 F（u，v）進行傅立葉逆變換得到的 f′（x，y）即為原始圖像的最佳估計。這個過程就是逆濾波的基本原理。在不考慮噪聲的情況下，g（x，y）=f（x，y）*h（x，y），則有

由式（4）可見，如果 H（u，v）在 uv 平面上取零或者很小，就會帶來計算上的困難，使復原結果與預期結果有很大差距。一般情況下，逆濾波器并不正好是1/H（u，v），而是 u 和 v的某個函數，可記為 M（u，v）。 M（u，v）常稱為復原轉移函數或處理傳遞函數。通常取M（u，v）為

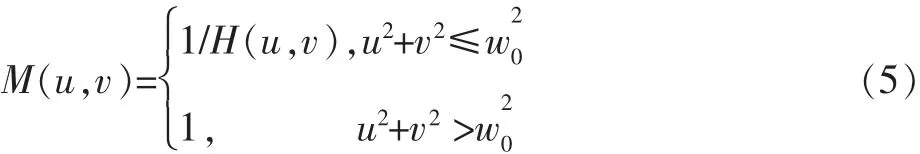
式中：w0的選取原則是將H（u，v）為零的點除去。這種方法使得復原結果的振鈴效應較明顯。改進的方法是取M（u，v）為

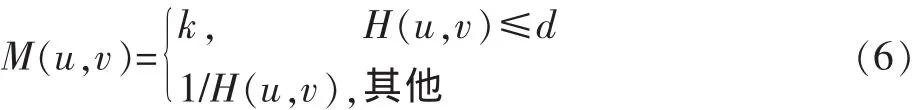
式中：k和d均為小于1的常數，而且d選得較小為好。

3 模糊原理及參數估計

3.1 離焦模糊圖像模型

在幾何光學條件下，對于線性移不變成像系統，離焦模糊圖像的退化模型可以抽象為一圓盤函數[4]

式中：r為退化模型唯一的模糊參數，是待求參數。對應的離散傅立葉變換可表示為[5]

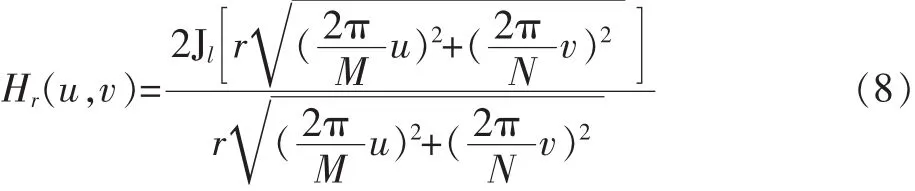
式中：Jl[]表示一階第一類貝塞爾（Bessel）函數，M和N為二維傅立葉變換尺寸。由一階第一類貝塞爾函數的性質可知，Hr（u，v）在頻率域的第一個暗環（零點）的軌跡為

根據式（9），可以由離焦模糊圖像的二維傅立葉變換頻譜圖G（u，v）的第一個暗環（零點）所對應的空間頻率u和v 求出模糊半徑 r，從而求出點擴散函數 hr（x，y）和 Hr（u，v）。

3.2 運動模糊圖像模型

對勻速運動模糊圖像來說，設物體沿水平方向移動了d個像素，則退化模型可以描述為[6]

式（10）對應的離散傅立葉變換可表示為[7]

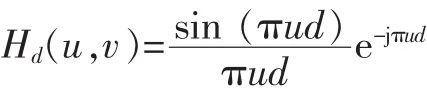
Hd（u，v）的頻譜幅值為。 由此可知，的零點位置分布在1/d的倍數處。零點所在頻譜圖像上體現為暗條紋，而曲線包絡的峰值點在頻譜圖像上體現為亮條紋。因此，只要求出條紋間距D，根據式（11）計算相移量 d，點擴散函數 Hd（x，y）和Hd（u，v）也就確定。

3.3 參數估計

對退化圖像做二維傅立葉變換得到退化圖像頻譜圖，再通過霍夫變換求取暗環半徑及條紋間距。求取暗環半徑過程如下:

1）對頻譜圖進行邊緣檢測得到邊緣圖像。

2）根據先驗知識，分別確定第一暗環半徑范圍，從而減小搜索半徑。

3）圓的參數方程可寫為：a=x-rcos θ，b=y-rsin θ。 將邊緣點代入式中求出參數（a，b）之值。由于圓心位于圖像中間區域的某個范圍，因此如果（a，b）位于這一范圍，則將相應的累加陣 H（a，b，r）中的元素加 1，否則加 0。

4）找出 H（a，b，r）中元素的最大值，即是對應半徑為r，圓心為（a，b）的暗環。

求取條紋間距過程與暗環半徑相似，不同的是直線參數方程表示為ρ=xcos θ+ysin θ。對檢測到的直線求取出直線間距，再利用公式（9）和（11）算出模糊半徑與相移量。

4 實驗結果

選用256×256的Lena圖像作為原始圖像，利用Hough變換在頻率域上估計退化參數，采用改進的逆濾波器對模糊圖像進行復原。表1與表2分別是利用Hough變換求取的暗環半徑和條紋間隔同實際大小的比較，可見，結果與真實值比較接近。圖1是模糊半徑為5及相移量為15的逆濾波復原結果。

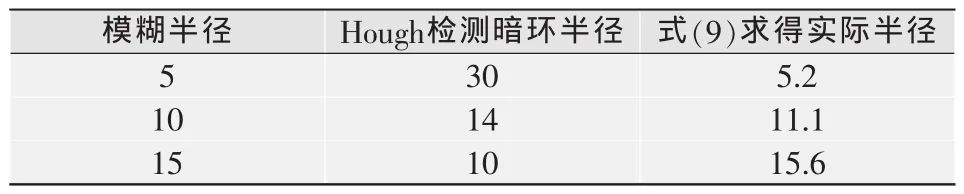
表1 利用Hough變換求取的暗環半徑同實際大小的比較

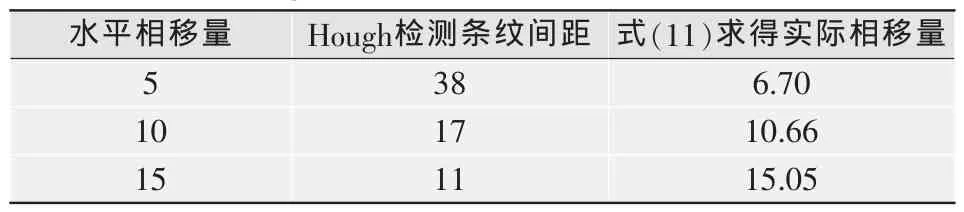
表2 利用Hough變換求取條紋間隔同實際大小的比較

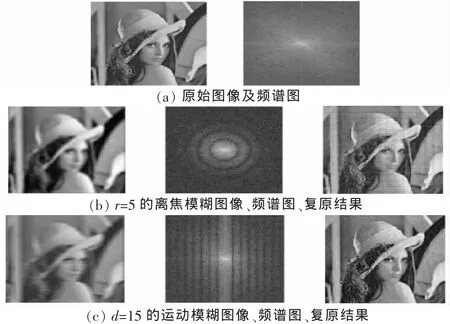
圖1 Lena圖像實驗結果

圖像的復原效果比較好，不過在圖像中仍然存在一些振鈴波紋，可采用巴特沃斯低通濾波器等對圖像進行處理，從而減小振鈴波紋現象。實驗結果表明，改進的逆濾波器簡單易實現，復原結果較好。但Hough變換估計退化參數的準確性有待進一步提高。

5 小結

數字圖像復原是圖像處理中的一項重要技術。筆者采用改進的逆濾波器，避免了一般逆濾波器的普遍病態性，算法簡單易實現，且計算運行時間少。實驗結果證明了該方法的可行性和有效性，適用于模糊圖像的快速復原。

[1]張雪峰，張全法，馮小星.一種掃描圖像幾何畸變的數字校正方法[J].電視技術，2003（9）：78－79.

[2]OMG.The Common Object Request Broker:Architecture and Specification：Version 3.0[S].2002.

[3]CONZALEZ R C.數字圖像處理[M].北京：電子工業出版社，2003.

[4]PAVLOVIC G，TEKALP A M.Maximum likelihood parametric blur identification based on a continuous spatial domain model[J].IEEE Trans.Image Proc.，1992，1（10）:496-504.

[5]LAY K T，KATASGGELOS A K.Image identification and restoration based on the expectation-maximization algorithm [J].IEEE Trans.ASSP，1990，38（7）:1180-1191.

[6]LOKHANDE R.Identification of parameters and restoration of motion blurred images[M].[S.l.]： ACM Press，2006:301-305.

[7]王文發，劉彥保.傅立葉變換用于圖像處理時的特性分析[J].延安大學學報，2006，25（3）：22-24.