管涌動態發展模型中的非線性滲流研究

羅德兵

（澧縣澧陽大垸水利管理委員會 常德市 415500）

汛期洪水對土石壩特別是雙層地基的江河大堤威脅最大的是管涌[1]。管涌一般都是非線性滲流，線性問題只是非線性問題的特例，且適用條件極其有限。在多孔介質的滲流中，達西定律是最基本的本構關系，達西定律的表達式為：V=-KJ。式中K稱為滲透系數或水力傳導系數。通常，對于固定不變的介質與性質不變的流體，K值不再發生，則稱線性滲流。在恒定水頭的作用下，管涌的形成與發展是一個動態的發展過程，不但滲透系數在不斷地變化，水力梯度也隨著多孔介質性質的變化而變化。因此，管涌是非線性滲流的一種，柴軍瑞[2]將其劃分為流態非線性問題。管涌動態發展的過程不僅僅存在流態非線性問題，還存在多重非線性問題的耦合作用。

1 基本概念

對多孔介質與滲流流體的概念與性質，文獻[3～4]中有較詳細的描述。現主要強調以下幾個基本概念，以助于對管涌動態發展模型的理解。

（1）多孔介質的滲透性。

在達西定律中的常數K，通常稱為滲透系數。經證明，常數K不僅與多孔介質的性質有關，還與流體的粘滯系數成反比。設流體的粘滯系數為v時，在同一種多孔介質相同的運動狀態下，對不同的流體參數k=K/v相同。因此，K又稱水力傳導系數，k稱為多孔介質的物理滲透性[5]。

（2）多孔介質的比面與迂曲度。

比面和迂曲度是刻畫在多孔介質運動流體與介質發生作用頻數的重要參數[6]。比面為單位體積多孔介質內孔隙的表面積，記為Σ。迂曲度為流體的路徑長度與樣品長度之比的平方，即為流體路徑長度與其位移矢量模長之比的平方，記為τ。

（3）滲透力。

滲透力是流動著的流體對固體介質的作用力，除與滲透水力坡降、流體性質等因素相關外，對單顆粒而言，它是與顆粒表面積成正比的，可以認為是面力。但對多孔介質而言，它與介質的總表面積成正比，而總表面積是對比表面積進行體積積分，與介質的體積成正比，因此，可以認為它是體力。

2 管涌發展中的非線性滲流問題

對管涌動態發展模型滲流的非線性作用，主要有以下幾種因素：

（1）滲流流體性質的非線性變化。

管涌發生后，流體由原來的純水變化為包含部分固體顆粒的混合流體，這種流體的粘滯系數也會隨之變化。而且，由于固體顆粒與水體之間存在相對運動，粘滯系數的變化也變成非線性作用。

（2）滲流空間的非線性變化。

在管涌發生的過程中，由于固體顆粒在多孔介質中存在起動與止動的情況，即流體對固體顆粒存在“搬運”作用。因此，分別對于流體與固體來說，其連續性方程存在非線性迭代問題。當靜止顆粒起動時，孔隙比增加，土體內含水量也相應增加，起動的固體顆粒又占據了運動著的流體中的部分體積。當運動顆粒被其他顆粒吸附靜止時，孔隙比減少，土體內含水量也相應減小。

（3）固體介質滲透系數的非線性變化。

滲流空間的非線性變化帶來的另一個問題是固體介質滲透系數的非線性變化。固體顆粒的起動與止動過程都會改變多孔介質的固體顆粒與孔隙之間的關系，使固體介質的物理滲透性發生了變化。

（4）本構關系的非線性變化。

達西定律的理論推導的前提條件是滲流流體的運動狀態為層流狀態，流體在層流狀態下要使其滲透作用力達到顆粒的起動作用力的可能性是比較小的。因此根據基于管流狀態的尼古拉茲實驗可知，當流體流速達到某一數值后，其沿程阻力不再與趨向于與流體流速的平方成正比。由此，修正的紊流狀態下的達西公式也不再是線性關系。

3 滲流流體性質的非線性變化

混有固體顆粒的流體性質的變化規律，可按混溶型流體與非混溶型流體兩種方法進行探討。

3.1 混溶型流體

滲流流體性質的非線性變體主要是指對混溶有固體顆粒的流體，其性質的變化主要表現為粘滯系數和流體密度的變化。

3.1.1 混溶型流體的假設

混溶性流體的粘滯系數變化理論主要來源于目前的泥沙研究。愛因斯坦[7]、錢寧、萬兆惠[8]、沙玉清[9]等對混溶性流體的性質做了研究。采用這種方式進行計算與分析有如下的假設條件：

（1）把流體做為一種混合流體來看待，即在流體運動的過程中，固體顆粒是完全溶在流體里的，它們之間沒有相對的運動。

（2）流體與固體介質之間存在固體顆粒的物質交換。流體與固體之間發生物質交換后，它們相應的性質發生了變化。

3.1.2 流體粘滯系數

針對流體性質隨固體顆粒含量的變化而變化的規律，存在以下兩類描述：

（1）粘滯系數的線性變化。

愛因斯坦總結水體粘滯系數與體積含沙量之間有如下的關系：

當考慮這種流體也是對簡單非線性問題的理想化與線性化。它只適用于固體顆粒含量較少的情況。粘滯系數與流體體積含沙量之間的線性關系并不能說明滲流形態的線性關系。

（2）粘滯系數的非線性變化。

目前已有大量學者根據實驗總結出粘滯系數的非線性變化規律。包括二次多項式、指數形式等。

3.1.3 流體密度

混溶性流體密度表達式：

式中 ρ0、ρ——純流體與混合流體的密度；

γs——固體顆粒浮容重；

Sr——混合流體中顆粒的體積飽和度。

3.2 非混溶型流體—基于顆粒流理論

顆粒流最先由Cundall P A,Strack O D L[10,11]等提出。周健[12～14]、曾遠[15]、張剛[16]等對其進行了總結，將其應用于管涌的運動狀態中。其基本點是分別對純凈流體與固體顆粒進行考慮時的非線性變化規律研究。流體按純流體考慮，對溶入流體在顆粒分別進行受力分析，并對所有顆粒作用的總和進行積分求和，然后將作用反過來施加給流體。該過程本身就是一個復雜的非線性作用的過程。

3.2.1 顆粒流的基本理論

顆粒流考慮顆粒之間的相互碰撞及固體顆粒與流體之間的相互作用。并基于牛頓第二運動定律、力一位移定律(廣義胡克定律)及牛頓流體的本構關系建立固固、固流相互耦合的本構關系。

3.2.2 顆粒流基本的方法與假設

基本假設包括：

（1）顆粒單元為剛性體；

（2）接觸發生在很小的范圍內，即點接觸；

（4）接觸處的特殊的接觸強度；

（5）顆粒單元為圓形。

接觸過程滿足如下假設：線性彈簧或Hertz-Mindlin法則；庫侖滑塊；可選擇的連接類型,如一種是點接觸；另一種是用平行的彈簧連接,這種平行的彈簧連接可以抵抗彎曲。

它們的作用力都會反作用于運動著的純流體上。對自由運動顆粒的作用可以看成是作用在流體內部的體積力，將滾動顆粒與滑動顆粒的作用看成是流體表面的面積摩擦力。

3.2.3 固相的運動方程

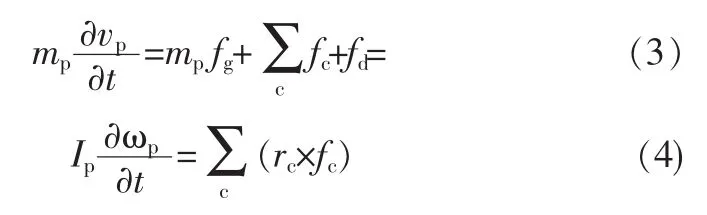
式中vp——顆粒速度矢量；

近年來，數字貨幣發展迅猛，帶來了一系列的投資機會，收益豐厚，但也帶來很大的金融風險，尤其是對比特幣的炒作，引發了金融市場尤其是數字貨幣市場的恐慌。世界各國都在完善對數字貨幣的監管，數字貨幣將來也有可能代替流通的紙幣，發揮貨幣的職能，但這將是一個漫長的過程，需要世界各國共同加強對數字貨幣的研發和監管，防止以此引發金融危機。

ωp——顆粒轉動速度矢量；

mp——顆粒的質量；

Ip——顆粒的轉動慣量；

fg——重力加速度矢量；

fc——接觸c（c=1，2，）處顆粒之間的接觸力；

rc——接觸c處指向顆粒形心的方向矢量；

fd——流體施加于顆粒p的拖曳力，包括浮力與液一固之間的相互作用力。

3.2.4 液相的運動方程

流體運動的納維—斯托克斯公式中，將流體速度的隨體導數按時間與空間分別求導，考慮流體的粘滯系數有可能發生變化，因此，速度的拉普拉斯算子按剪應力張量的變化率代替，并增加流體與固體結構的相互作用，即得到下式：

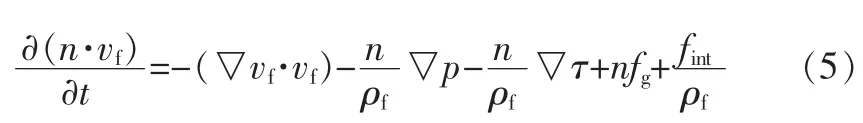
式中n=n（x，t）——孔隙率；

（x，t）——空間和時間的坐標；

vf=vf（x，t）——平均流體速度矢量；

△p——壓力梯度；

τ——平均流體應力張量；

fg——重力加速度矢量；

fint——液一固之間的相互作用力矢量。

4 滲流空間的非線性變化

滲流空間變化的非線性主要指泥沙起動與止動時流體運動的空間發生了變化。

4.1 泥沙顆粒的起動

4.1.1 前期學者的理論成果

對于單個顆粒的臨界起動條件，太沙基[17]、扎馬林、沙金煊[18]、毛昶熙[19～21]、劉杰[5]、丁留謙[22]等都取得了大量成果。他們總結了大量臨界水力坡度的公式，其中大部分都是從豎直向上的方向考慮管涌的形成。

4.1.2 建議的統一公式

考慮自由顆粒管涌發生在任何可能方向，形成管涌的泥沙起動前的圍壓力隨時間成指數變化，并考慮顆粒間的相互粘滯力時，按臨界平衡推導出下式：

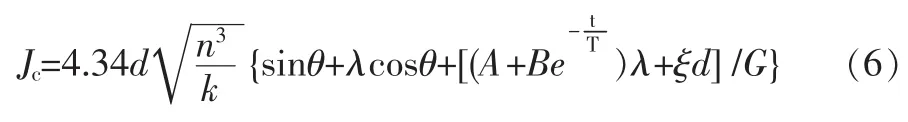
式中Jc——某個顆粒的臨界水力坡降；

d——其等效粒徑；

n——孔隙率；

k——滲透系數；

θ——管涌方向與水平的夾角；

λ——土體內摩擦系數，可取λ=tanφ；

ξ——顆粒間范德華力的系數[23]。

4.2 泥沙顆粒的止動

在流體中運動的顆粒會因為種種原因有一部分由運動狀態變為相對靜止，停留在滲流場的某個位置。這不僅減少了流體運動的范圍，還增加了固體的體積。因此，它對管涌發展滲流場的影響也是非線性的。

4.2.1 基于顆粒流的碰撞理論

顆粒流最初的模型源于土體的剪切破壞。在土體的剪切破壞中，外加了一個已知運動軌跡的部分做為邊界條件，稱為墻體。外部對墻體的約束是剛性的，由此墻體不滿足運動方程。顆粒流固相的基本運動方程是式（3）、式（4）。

在顆粒流的理論中，每一個顆粒的運動是連續的，顆粒與墻體的碰撞是顆粒靜止下來的主要原因。與流體內顆粒與顆粒碰撞相似，顆粒與墻體的碰撞過程也做了相應假設。碰撞的力學特性與顆粒間的碰撞相似。由于墻體表面法向方向一般與顆粒的運動方向會成一定角度，因此，可將其作用力分解為法向方向作用力與水平方向作用力。并在這兩個方向對顆粒采用運動方程進行分析，確定碰撞后顆粒的運動狀態。

4.2.2 基于隨機過程的運動理論

顆粒流中對每一個顆粒都必須采用連續的運動方程，計算量大。對所有顆粒都是球形的假設與實際的顆粒運動狀態可能會有一定的偏差。有必要尋找其他的運動模型來彌補其不足。曹敦侶[24]建立了管涌發展過程的隨機模型。

在隨機過程中，存在大量隨機因素影響事物的運動狀態，我們需要對這些隨機因素進行分類與比較，并確定這些因素的分布形式、對事物運動狀態的影響大小等。

首先，需要確定在一個單元體內運動著的固體顆粒的粒徑分布與顆粒的運動速度，根據式（6）的起動公式，可以大致估計顆粒的粒徑分布，對不同粒徑的顆粒需要根據滲流路徑與水力梯度估算其流速的分布。

其次，需要估計顆粒的形狀與屬性，以確定顆粒的運動形式。文獻[7]對單個顆粒形狀有詳細的描述。流體中包含的顆粒運動形式一般可分為自由運動、滑動與滾動等三種形式，小粒徑多以自由運動為主，大粒徑球形多以滾動為主，塊形多以滑動為主。

最后，還需要對多孔介質的某些屬性做一些統計與描述。如多孔介質的比面與迂曲度有關。多孔介質的孔隙特性、有可能形成管涌的通道的特性等。

根據以上分析，在一個單元內確定的水力梯度與滲流特性的前提下，可以建立關于顆粒粒徑、形狀參數與多孔介質特性等參數相關的微分方程式，用來判斷顆粒運動過程中與通道發生碰撞次數的概率及靜止下來的可能性。然后對各組粒徑與各種形式進行累加、積分。求解顆粒靜止下來的概率。

5 固體介質物理滲透性的非線性變化

建立固體孔隙特性與物理滲透性之間的關系式。目前已有大量的經驗公式，常用的有與d17、d20、d50及孔隙平均孔徑相關等多種表達形式。劉杰[4]基于層流狀態毛細管管流的推導公式如下：

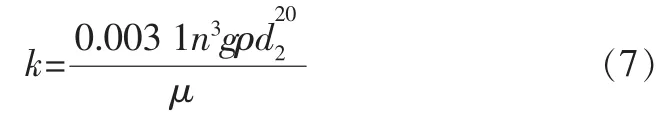
在管涌的發展過程中，必須考慮孔隙的不均勻性，會使總體的物理導滲性增加。建議根據不同的破壞程度在上式乘以一個大于1的系數。

6 本構關系的非線性變化

流體在層流運動狀態下運動時，即不考慮雷諾切應力。顆粒在豎直方向受到的向上的作用力為流體上下速度差引起的壓力差。當顆粒密度按計時，不考慮顆粒間的相互粘滯作用時顆粒起動的流體速度平方的臨界梯度計算可得：

按此式的判斷，豎直方向上層流狀態下發生管涌的可能性較小。而現實工程中由于雙層地基與土體橫觀各向同性的影響，管滲多向水平與豎直方向發展，而豎直發展的情況更多。因此，管滲多發生在紊流狀態。

（1）層流狀態下的滲流的本構關系。

層流狀態下的本構關系即為達西定律。

（2）紊流狀態下的滲流的本構關系。

尼古拉茲在做管流實驗時總結出紊流狀態下流體壓力梯度與速度的平方成正比。目前，有學者又提出二項式公式、指數公式[25]及與加速度相關等多種公式。

7 管涌動態發展模型的求解思路

上述的幾個非線性問題是相互聯系與相互作用的。從成因上來說，流體運動的空間發生了非線性的變化，使流體與多孔介質之間存在相互的物質交換。這對流體來說，流體內部純流體與混溶的固體顆粒之間的相對運動變得更加復雜，從而改變了流體對外表現出的性質：粘滯系數。對多孔介質來說，改變了多孔介質中的孔隙比與孔隙形狀，從而改變了多孔介質的物理滲透性。滲流速度與水力坡降之間的非線性關系直接影響著上述一系列非線性相互作用，運動流體的水力梯度是顆粒沿水流方向受力的根本原因，孔隙內流體的速度平方的梯度是顆粒沿水流垂直方向受力的根本原因。流體粘性的變化與固體介質物理滲透性的變化又直接導致了水力傳導系數的變化，水力傳導系數直接反映不水力梯度與流體速度之間的變化規律。因此，由于上述幾個問題之間存在相互耦合作用，管涌動態發展的過程是一個相對復雜的多因素耦合的非線性問題。

解決上述多相滲流的非線性問題，主要有以下幾種方法：

（1）混溶性單相滲流——協同無機化學反應。

將溶有固體顆粒的流體看成單一性質的流體進行計算。在計算的過程中，流體與固體之間存在著物質的交換。物質交換的方向（是固體顆粒被流體沖走，溶入固體，還是溶于流體中的固體顆粒沉積下來，形成固體）、物質交換的頻繁程度都取決于流體與固體的性質、流體的流速等因素。物質交換的直接后果是導致固體導滲性質與流體性質的變化，從而形成一個簡單的耦合運動。

與無機化學反應的反應速度、焓變與熵變等概念相類似，我們可以將物質交換速度看成是化學反應速度，將流體及溶于其中的固體顆粒看成化學反應中的溶液，將多孔介質看成化學反應中的未溶固體，多孔介質的性質與固體的可溶性相類似，流體的水力坡降與滲流速度與化學反應的溫度與催化劑相類似。這樣，便可建立交換速度的平衡方程。從而模擬管涌現象的發生與發展過程。此交換速度需要做大量的實驗后總結歸納出經驗公式。與無機化學反應的主要區別是不斷有純滲流流體摻入滲流場，也不斷有固體顆粒帶出滲流場，即發展方向的不可逆性。

顯然，純流體與固體顆粒不發生相對運動的假設是這種計算方法最大的缺陷。

（2）多相滲流流體間的驅替理論。

目前，石油部門對水、油混合物的多相滲流所采用的方法多為多相滲流流體間的驅替[26～28]。考慮兩種互不混溶的流體在同一固體介質中的運動分析方程。其基本原理是基于不同流體混合時濃度差的基質吸力，驅替靜止孔隙與流體運動孔隙之間流體相互交換。

采油與管涌的發展模型相比較有三個相同點：

●它們都是由純水流帶動或驅替另一種物體運動；

●它們都具有不均勻的濃度，即存在基質吸力；

●它們都是不可逆過程。

毛細管水油驅替中的基質吸力主要來源于濃度差的壓力梯度、界面的表面張力及毛細管吸力等。考慮管涌發展過程中的多相滲流，基質吸力可以看成是總水頭相同的流動孔隙與靜止孔隙之間的壓力差。可將管涌過程中可能運動的固體顆粒（自由顆粒）看成是起動滲透壓力較大的Bingham流體。建立無窮維的驅替模型。并用體積含沙量作為刻畫流固驅替的程度與標志。

顯然，采用這種方法只能近似模擬管涌的動態發展過程。

（3）顆粒流數值解法。

基于顆粒流的基本概念與基本假設的條件下，建立的微分方程。顆粒流的程序已開發出PFC2D與PFC3D等二維、三維程序。周健、張剛[15]等學者將顆粒流在基本概念與管涌形成的機理相結合，提出了管涌的顆粒流發展模型。目前已采用PFC程序做出管涌動態發展模型。

（4）多種非線性滲流的耦合分析方法。

根據以上各種引起非線性的不同因素,建立微元體內：水頭—流速—流體與固體的交換—流體內顆粒流的運動及相互作用—固體導滲性質的變化—確定滲流的本構關系—重新計算水頭的循環過程。在循環計算的過程中，需要對運動的顆粒按運動狀態與顆粒粒徑進行統計分析并分類計算，確定起動與沉降的可能性，進而確定固體與流體的物質交換強度。在這方面的無單元法的有限元計算，周曉杰[29]作了初步研究。

（5）管涌動態發展的動力系統分析法。

管涌發展到一定程度（或經處理）后，在出滲區附近形成的通道會調整滲流場的各種參數。下游有可能形成相當于褥墊的排水體，而形成不會發展的無害管涌。這種管涌的發展具有一類穩定的吸引子。即這種管涌的外部荷載在滲流場本身微分算子的收斂區域即譜半徑的范圍內。

研究管涌動態發展模型的目的管涌發展的穩定性，其次是判斷我們所研究的大堤或大壩抵抗管涌變形的時間，即工程抵抗管涌的使用壽命。如果系統不具有整體吸引子，即微分算子在給定水頭作用下始終會破壞，那么，我們還需要根據微分算子的發散程度，以時間為計算步，確定系統的發散程度。如果我們能夠判斷大堤或大壩（或經處理后）在設計荷載作用下其滲透變形具有穩定的吸引子，問題即得到解決。如果不能收斂，我們需要估算系統的使用壽命。

8 結 語

管涌的發展過程受多方面非線性因素的影響。求解管涌發展動態過程的模擬也相當復雜。以上幾種計算方式各有所長。雖然第一、二種方法存在缺陷，但做了大量簡化，計算更方便。采用墻體的形式定義土體中承受土壓力的骨架顆粒不是很合適，骨架顆粒與其他堆積在一起處于相對底層的細顆粒之間有可能有相對于顆粒重力大得多的作用力，隨著管涌的發展，這些顆粒的起動對骨架的作用可能不僅僅是對墻體（不動體）的作用。顆粒體形也千奇百怪，不可能完全是圓球形，顆粒形狀在很大程度上影響了其運動形式，在管涌發展過程中，只有位于大孔徑孔隙或臨空界面表面的顆粒起動后，其下層的顆粒才有可能起動，因此管涌初期只是個別顆粒的個別運動。等等這些因素都是顆粒流與管涌動態發展過程存在的微小差別，且顆粒流的計算量大，第三種方法也有需要改進的地方。第四種方法計算量大，需要確定的參數與方程多，采用非線性計算程序還很不成熟。第五種方法需要從動力系統與混沌學的角度，將影響管涌發展的各種因素換算成一個復雜的微分算子的作用，然后判斷其抵抗外界荷載的譜半徑或整體吸引性。應該是一種可能應用于實際的比較理想的方法。

1 中華人民共和國水利部.中國’98大洪水.中國水利年鑒1999[M].北京:中國水利水電出版社,1999.

2 柴軍瑞.巖土體水力學非線性問題[J].巖土力學,24(增).2003.159－161.

3 貝爾.李競生，陳崇希譯.多孔介質流體動力學[M].北京:中國建筑工業出版社，1983.

4 薛定諤.王鴻勛，張朝琛，孫書琛譯.多孔介質中的滲流物理[M].北京:石油工業出版社,1982.

5 劉杰.土石壩滲流控制理論基礎及工程經驗教訓[M].北京:中國水利水電出版社，2006.

6 孔祥言.高等滲流力學[M].北京:中國科學技術大學出版社，1999.

7 愛因斯坦.錢寧譯.明渠水流的挾沙能力[M].北京:水利出版社，1956.

8 錢寧，萬兆惠.泥沙運動力學[M].北京:科學出版社，1983.

9 沙玉清.泥沙運動學引論[M].北京:中國工業出版社，1965.

10 Cundall P A,Strack O D L.Particle flow code in 2 Dimensions[A].Itasca Consulting Group,Inc.,1999.

11 Cundall P A,Strack O D L.A discrete numerical model fgraunlar assemblies[J].Geotechnique,1979,29(1):47-65.

12 周健，池永.土的工程力學性質的顆粒流模擬[J].固體力學.2004,25(4):377-382.

13 周健，池永，池毓蔚，等.顆粒流方法及PFC2D程序[J].巖土力學，21(3)2000：271-274.

14 周健，池永.砂土力學性質細觀模擬[J].巖土力學，2003，24(6):901-906.

15 曾遠.土體破壞細觀機理及顆粒流數值模擬[D].上海：同濟大學，2006.

16 張剛.管涌現象細觀機理的模型試驗與顆粒流數值模擬研究[D].上海：同濟大學，2007.

17 太沙基潑克.蔣彭年譯.工程實用土力學[M].北京:水利出版社,1960.

18 沙金煊.多孔介質管涌研究[J].水利水運科學研究，1981（3）:89-93.

19 毛昶熙.滲流計算分析與控制[M].北京:水利電力出版社，1990.

20 毛昶熙.管涌與濾層的研究:管涌部分[J].巖土力學,2005，26(2)：209-215.

21 毛昶熙，等.堤基滲流管涌發展的理論分析[J].水利學報，2004，12（12）：46-50.

22 丁留謙，等.雙層堤基管涌動態發展的有限元模擬[J].水利水電技術,2007，38(2)36-39.

23 唐存本.泥沙起動的規律[J].水利學報,1963，4（2）：1-12.

24 曹敦侶.滲流管涌的隨機模型[J].長江科學院院報,1985,(2).

25 代群力.地下水非線性流動模擬[J].水文地質工程地質.2002(2)：50-55.

26 FAL Dallien.范玉平等譯.現代滲流物理學[M].北京:石油工業出版社，2001.

27 陳鐘祥，劉慈群.雙重孔隙介質二相驅替理論[J].力學學報，1980,12(2)：109-119.

28 劉慈群，郭尚平.多重介質滲流研究進展[J].力學進展，1982,12(4).360-364.

29 周曉杰.堤防的滲透變形及其發展的研究[D].北京：清華大學，2006.