EM算法優化WDRNN短期負荷預測模型①

劉遠龍，龔文杰，徐 超，張智晟

(1.青島供電公司，青島 266002;2.青島大學自動化工程學院，青島 266071)

隨著現代電力系統的不斷發展，尤其是電力市場競爭機制的引入，電力系統短期負荷預測STLF(short-term load forecasting)具有重要的理論意義和高的經濟價值，提高預測精度符合當前電力系統的實際需要。

基于BP算法的多層前饋神經網絡FNN(feedforward neural networks)原理已在國內外電力系統ST LF中得到廣泛的研究與應用[1]。但應指出，FNN本質是屬于靜態非線性映射關系，它更適用于處理與時間無關的對象。電力系統負荷序列性質屬于混沌時間序列[2～4]，是典型的非線性動力學時間序列，需用動態遞歸神經網絡進行建模研究，動態遞歸神經網絡能更直接的反映系統的動態特性。本文所提出的小波對角遞歸神經網絡WDRNN(wavelet diagonal recursive neural network)就屬于動態遞歸神經網絡的范疇。

神經網絡的學習算法研究成為該領域的研究熱點，并取得了較為顯著的效果[5，6]。類電磁機制EM(electromagnetism-like mechanism)算法是由Birbil和Fang提出的一種新的全局優化算法[7]。該算法具有全局優化能力強，編程實現簡單，收斂性好等優點，其收斂性已得到理論證明[8]。EM 算法已被應用于函數優化[9]、流水車間調度[10]和車輛運輸路線規劃[11]等問題的研究中，取得了較好的效果。但目前該算法在電力系統領域應用還比較少。本文采用EM 算法訓練WDRNN，通過實際地區電網的負荷的預測仿真和測試，證實所提出的基于EM算法的WDRNN模型能有效提高預測精度。

1 WDRNN預測模型構造及數學描述

動態遞歸神經網絡即在神經網絡NN(neural networks)內部引入反饋使NN具有動態性能，能更直接地反映系統的動態特性，它是依賴NN內部神經元間狀態的反饋來描述動態行為，即用較少的記憶單元來描述非線性系統的動力學特性，無須存儲所有的輸入信息，且又能在網絡中反映出系統所有歷史信息對當前系統響應的影響。

對角遞歸神經網絡是一種特殊的動態遞歸神經網絡，它與FNN相同之處是都有輸入層、隱含層和輸出層;兩者的區別在于對角遞歸神經網絡的隱含單元具有自反饋。對角遞歸神經網絡的動態映射和記憶功能正是通過遞歸神經元在內部的反饋回路捕捉系統的動態特性來實現的[12，13]。本文提出的WDRNN模型(見圖1)是對常規對角遞歸神經網絡模型的改進。

圖1中，m、l分別表示WDRNN模型的輸入層和隱含層節點個數，輸出層節點個數為1(單步預測)。ui(k)表示第i個輸入節點在k時刻的輸入，WIH和WHO分別表示輸入層節點到隱含層節點以及隱含層節點到輸出層節點之間的連接權重。WHH表示隱含層節點之間的連接權重，WHR表示隱含層節點自身的自反饋。若(k)表示隱含層第j個節點在k時刻的輸出，用(k)表示隱含層第j個神經元在k時刻的內部狀態，則可表述為

式中:fN為小波基函數，aj(k)和bj(k)分別為在k時刻小波基函數的伸縮因子和平移因子。小波基函數本文選用Morlet母小波基函數，可表示為

若用y(k)表示輸出層神經元在k時刻的輸出，則可表述為

圖1 WDRNN預測模型結構Fig.1 Structure of WDRNN forecasting model

2 EM算法及對WDRNN模型的優化

EM算法是模擬電磁場中帶電粒子間的吸引與排斥機制，把每個搜索粒子類比成空間中的一個帶電粒子，每個粒子的電荷由待優化的目標函數的函數值決定。電荷值決定了該粒子對其他粒子的吸引或者排斥的強弱，目標函數值越優，吸引就越強。EM算法利用電荷為每個粒子下一步的移動尋找方向，即通過計算其他粒子施加給當前粒子的合力來確定這個方向。同電磁力的計算方式一樣，該合力是通過將來自其他粒子的力進行矢量疊加而得到的。

圖2選取了3個粒子說明粒子間如何依據吸引與排斥機制進行搜索。設粒子2表示的解優于粒子1表示的解，而粒子3表示的解劣于粒子1表示的解，那么粒子2將對粒子1有一個吸引力F21，而粒子3將對粒子1有一個排斥力F31，這兩個力疊加得到的合力F1就將確定粒子1移動的方向，這樣促使粒子向較優的區域移動。

圖2 粒子吸引與排斥機制示意Fig.2 Schematic diagram of attraction and repulsion mechanism for particles

2.1 EM算法優化WDRNN流程

在負荷預測模型中，給定的預測訓練樣本集用S={(Ui，Yi)|i=1，2，…，n}表示，其中Ui是輸入樣本，Yi是對應的輸出樣本，n是預測樣本個數。

對WDRNN的連接權值(包括輸入層節點到隱含層節點之間的連接權重WIH、隱含層節點到輸出層節點之間的連接權重WHO、隱含層節點之間的連接權重 WHH、隱含層節點自身的自反饋WHR)，小波基函數的伸縮因子aj和平移因子bj，分別采用十進制進行編碼，構成粒子。

EM 算法優化WDRNN，主要由四個基本步驟組成，即初始化、局部搜索、計算合力以及移動粒子。具體流程如圖3所示。

圖3 EM算法優化WDRNN流程Fig.3 Flow chart of optimizing WDRNN by EM algorithm

2.2 初始化

初始化就是從已知可行域中隨機選取s個粒子X1，X2，…，Xi，…，Xs，計算每個粒子的目標函數值 f(Xi)，并將目標函數值最優的粒子記為Xbest，表示當前最優粒子。

2.3 局部搜索

對于EM算法，局部搜索為種群的全局搜索提供了有效的局部信息，這使得算法既具有全局搜索能力，又具有局部區域精細搜索能力。本文局部搜索策略采用隨機線性搜索的方法[7]。簡述如下。

對種群中粒子 Xi=(xi1，xi2，…，xij，…，xip)的各分量按照隨機步長進行一維搜索，用更優的粒子替換當前粒子，對第i個粒子第j個分量xij的搜索過程如下:

(1)均勻產生(0，1)之間的隨機數λ1和λ2，令yj=xij;

(2)若 λ1 ＜0.5，則 yj=xij-λ2(xij-lij);否則，yj=xij+λ2(uij-xij)。其中，lij表示第i個粒子第j個分量的下邊界，uij表示第i個粒子第j個分量的上邊界。

對第i個粒子的每個分量都進行如上搜索，搜索完畢后，得到搜索后的粒子Y=(y1，y2，…，yj，…，yp)，求取其目標函數值 f(Y)，若 f(Y)≤f(Xi)，則更新粒子，即Xi=Y，否則不更新粒子。

2.4 計算合力

EM算法中合力計算是對電磁場中吸引與排斥機制的模擬。通過計算合力，將粒子所獲得的局部信息與全局信息結合起來。由電磁理論中的疊加原理可知，一個粒子受到的其他粒子施加的電磁力與粒子之間的距離成反比，與它們所帶電荷量的乘積成正比。

1)計算粒子電荷量

計算合力前，應先求取每個粒子所帶的電荷量，粒子的電荷量決定了自身所受吸引力或排斥力的大小，同時影響其他粒子所受吸引力或排斥力的大小。第i個粒子Xi的電荷量qi的計算式為

式中:s表示粒子的個數;p表示粒子的維數;f(Xi)表示第i個粒子的目標函數值;f(Xbest)表示當前最優粒子的目標函數值。通過式(5)可以看出，目標函數值較優的粒子電荷量較大，具有更強的吸引力或排斥力。

2)計算合力

電荷量計算完成后，模擬電磁理論中的庫侖定律，作用在第i個粒子上的合力Fi計算式為

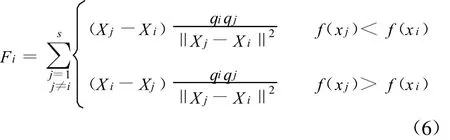
根據式(6)，每兩個粒子之間，目標函數值較優(即較小)的粒子將吸引另一個粒子;目標函數值較劣(即較大)的粒子將排斥另一個粒子。由于當前最優粒子Xbest的目標函數值最小，所以它充當著一個絕對吸引的粒子，吸引著種群中的其他所有粒子。

2.5 移動粒子

種群中的各粒子在合力的作用下移動。第i個粒子在合力Fi的作用下，按式(7)移動到新的位置，使粒子的位置得到更新。

式中:λ為0～1之間的隨機數;V為一個向量，表示向上邊界或下邊界移動的可行步長。

3 實際地區網日負荷預測與誤差分析

3.1 仿真測試預測模型構造的基本依據

采用相空間重構理論[2]計算飽和嵌入維數m及延遲時間τ，重構相空間，利用歐氏距離法求得預測相點的k個最近鄰相點，它們各對應的m+1個分量組成該預測相點的k個訓練樣本集，它是屬于動態步進跟蹤訓練，即所求得預測值加入到下一個預測點相的動態相軌跡中求得下一個預測相點的k個最近鄰相點。根據所求飽和嵌入維數m作為優化遞歸神經網絡預測模型的輸入層節點，輸出節點數為1。經相空間重構理論可以求得該地區電網負荷系統嵌入維數m=7，延遲時間τ=1 h。

本文通過模型1——基于BP算法的FNN預測模型、模型2——基于BP算法的DRNN預測模型、模型3——基于BP算法的WDRNN預測模型和模型4——基于EM算法的WDRNN預測模型四個預測模型在實際地區電網負荷系統中進行仿真測試進行比較。

模型1采用7-14-1結構的FNN模型，模型2采用7-8-1結構的DRNN模型，模型3采用7-8-1結構的WDRNN模型。3個模型都采用BP算法進行訓練，在仿真過程中，最大允許誤差 。學習率和動量因子分別取為0.10和0.90。模型4采用7-8-1結構的WDRNN模型，采用EM算法對WDRNN模型進行訓練，粒子個數取200。

3.2 地區電網的4種模型日負荷預測仿真

用4種模型進行小時/日負荷預測結果和誤差的比較，結果如圖4所示。

圖4 地區電網的4種預測模型的日負荷預測誤差和比較Fig.4 Daily load forecasting errors and comparison of four kinds of models in power network

通過地區電網負荷系統的4個模型的誤差性能綜合分析比較如表1所示。

表1 地區電網的4種預測模型誤差指標比較Tab.1 Error index comparison of four forecasting models in power network

從表1可知，基于BP算法的FNN預測模型1的誤差性能最差，平均絕對誤差為3.553%，最大相對誤差為8.529%。預測模型2采用了DRNN預測模型，平均絕對誤差比預測模型1降低0.609%，最大相對誤差比預測模型1降低1.561%，這是因為預測模型1的FNN屬于靜態NN，無法體現負荷的動態行為。而DRNN具有動態性能。預測模型3采用WDRNN，與采用DRNN的預測模型2相比，平均絕對誤差降低1.055%，最大相對誤差降低2.203%，表明WDRNN比DRNN具有更強的動態性能，對于預測精度的提高是有效的。預測模型4采用EM算法優化WDRNN，與采用BP算法的預測模型3相比，平均絕對誤差降低0.443%，最大相對誤差降低1.64%，是4個模型中預測精度最好的。可見，EM算法全局優化能力較強。

3.3 基于EM算法WDRNN預測模型的周預測誤差性能

為深入分析所提出的基于EM算法的WDRNN預測模型的性能，通過對某地區電網負荷系統進行一周預測，預測結果見表2所示。

表2 地區電網一周的預測誤差Tab.2 Daily load forecasting errors for a week in power network%

從表2可看出，基于EM算法的WDRNN預測模型具有較好的預測性能和預測穩定性。

4 結論

(1)小波對角遞歸神經網絡是對常規對角遞歸神經網絡的改進，改進策略一是在隱含層神經元之間增加了同層神經元之間的相互連接，使隱含層單元之間存在相互信息交換，使模型動態性能得到增強。改進策略二是隱含層函數用小波函數取代傳統Sigmoid函數，通過伸縮因子和平移因子的引入，使模型具有較強的逼近能力和容錯能力。

(2)EM算法作為一種新的全局優化算法，具有全局優化能力強，編程實現簡單，收斂性好等優點，可在電力系統其他領域推廣應用。

(3)經實際負荷系統預測仿真測試，獲得較滿意的預測精度，具有高的預測穩定性和良好的適應能力。

[1] Hippert H S，Pedreira C E，Souza R C.Neural networks for short-term load forecasting:A review and evaluation[J].IEEE Trans on Power Systems，2001，16(1):44-55.

[2] 李天云，劉自發(Li Tianyun，Liu Zifa).電力系統負荷的混沌特性及預測(The chaotic property of power load and its forecasting)[J].中國電機工程學報(Proceedings of the CSEE)，2000，20(11):36-40.

[3] 張智晟，馬龍，孫雅明(Zhang Zhisheng，Ma Long，Sun Yaming).混沌理論和支持向量機結合的負荷預測模型(Load forecasting model using chaos theory and support vector machine)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA)，2008，20(6):31-35.

[4] 鄭永康，陳維榮，蔣剛，等(Zheng Yongkang，Chen Weirong，Jiang Gang，et al).基于混沌理論的短期負荷局域多步預測法(Local-region multi-steps load forecasting model based on chaotic theory)[J].電力系統及其自動化學報(Proceedings of the CSU-EPSA)，2007，19(4):76-79.

[5] Yu Xinghuo，Efe M O，Kaynak Okyay.A general backpropagation algorithm for feedforward neural networks learning[J].IEEE Trans on Neural Networks，2002，13(1):251-254.

[6] Lera G，Pinzolas M.Neighborhood based Levenberg-Marquardt algorithm for neural network training[J].IEEE Trans on Neural Networks，2002，13(5):1200-1203.

[7] Birbil S I，Fang Shu-Cherng.An electromagnetismlike mechanism for global optimization[J].Journal of Global Optimization，2003，25(3):263-282.

[8] 王曉娟，高亮，陳亞洲(Wang Xiaojuan，Gao Liang，Chen Yazhou).類電磁機制算法及其應用(Electromagnetism-like mechanism with its application)[J].計算機應用研究(Application Research of Computers)，2006，23(6):67-70.

[9] 韓麗霞，王宇平(Han Lixia，Wang Yuping).求解無約束優化問題的類電磁機制算法(Electromagnetismlike mechanism algorithm for unconstrained optimization problem)[J].電子學報(Acta Electronica Sinica)，2009，37(3):664-668.

[10] Yuan Kun，Sauer N，Sauvey C.Application of EM algorithm to hybrid flow shop scheduling problems with a special blocking[C]∥IEEE Conference on E-merging Technologies and Factory Automation，Mallorca，Spain:2009.

[11] Wu Peitsang，Yang Kung-Jiuan，Huang Bau-Yuan.A revised EM-like mechanism for solving the vehicle routing problems[C]∥Second International Conference on Innovative Computing，Information and Control，Kumamoto ，Japan:2007.

[12] 段慧達，鄭德玲，劉聰(Duan Huida，Zheng Deling，Liu Cong).基于對角遞歸神經網絡的建模及應用(Modeling and application based on diagonal recurrent neural network)[J].北京科技大學學報(Journal of University of Science and Technology Beijing)，2004，26(1):103-105.

[13] Mu Yuqiang，Sheng Andong.Evolutionary diagonal recurrent neural network with improved hybrid EP-PSO algorithm and its identification application[J].International Journal of Innovative Computing，Information and Control，2009 ，5(6):1615-1624.