雷電流測量用大型Rogowski線圈輸出波形振蕩現象分析

周璧華 朱凱鄂 李炎新 郭建明

(解放軍理工大學工程兵工程學院,江蘇南京210007)

1.引 言

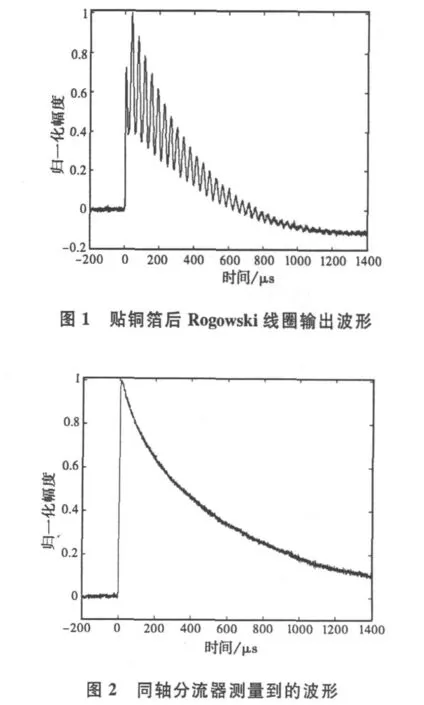
Rogowski線圈廣泛應用于脈沖大電流的測量中[1-2,4],當選擇Rogowski線圈測量柱狀高塔自然雷電流時域波形時,其內徑必須足夠大,文獻[3]通過增加線圈匝數獲得高電感,實現了測量結果的自積分,去除了外加積分器帶來的麻煩,同時可避免磁芯引入的非線性、磁飽和問題,從而為采用Rogowski線圈測量柱狀高塔自然雷電流找到了一種較好的手段。本研究為防止外界雜散電磁場對其測量結果的干擾,在該線圈的外面貼了一層銅箔作為屏蔽層。可實驗中發現,由于此屏蔽層的加入,使其輸出的電流波形疊加了高頻振蕩,如圖1所示,而同軸分流器測量到的波形如圖2所示。

為此,對Rogowski線圈的頻率響應及其影響因素進行了分析,考慮到銅箔與線圈之間的分布電容可能是引起附加振蕩的主要因素,為此建立等效電路模型,對該分布電容導致Rogowski線圈輸出波形出現振蕩的現象進行了分析,得出的結論證實了這一判斷,為下一步Rogowski線圈屏蔽設計的改進提供了依據。

2 自積分Rogowski線圈的測量原理

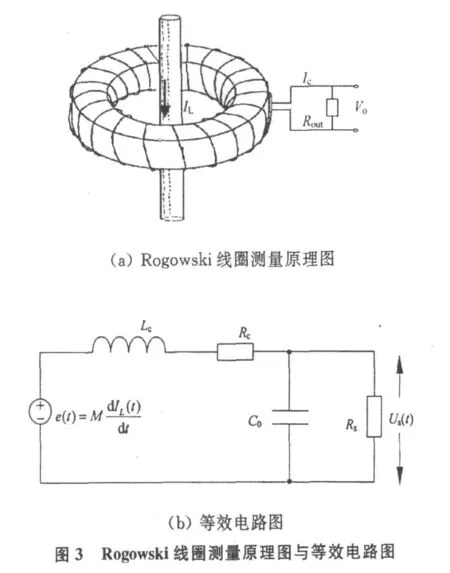
Rogowski線圈本質上是一種原邊為單匝,副邊為多匝線圈的電流互感器,如圖3(a)所示,通過測量變化電流I L產生的磁場在副邊線圈上的感應電壓來確定原邊線圈電流I L,圖3(a)中I c為線圈上的感應電流。其等效電路圖如圖3(b)所示[2-7],圖中Lc和R c分別為線圈的等效電感和電阻,C0為線圈的分布電容,R s為采樣電阻。

由電磁感應定律可得線圈上產生的感應電動勢為

式中,M為線圈與載流導體的互感系數。而由線圈的等效電路,在暫不考慮分布電容影響的情況下可得

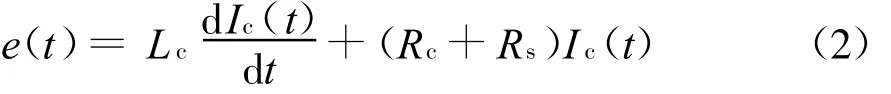
此時線圈工作在自積分狀態,無需外加積分電路。對角頻率為 ω的分量須滿足

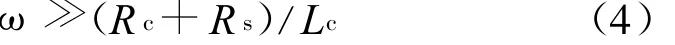
式(4)為自積分條件,并記 f l=(R c+R s)/(2πL c)為測量系統的下截止頻率。由于雷電流低頻成分豐富,為使線圈在測量雷電流時低頻失真減至最小,應使 fl盡可能低。為此,應盡量增大線圈的電感Lc,減小線圈的損耗R c及采樣電阻R s。

3 分布電容對Rogowski線圈動態特性的影響

線圈的分布電容會影響線圈的高頻特性[5]。如果考慮分布電容的影響,由圖3(b)可知,流過線圈的感應電流I c(t)為

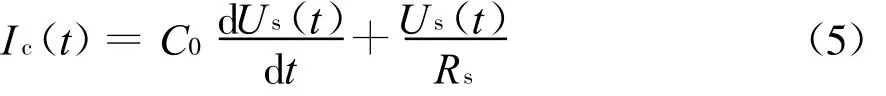
建立回路電壓方程并化簡得

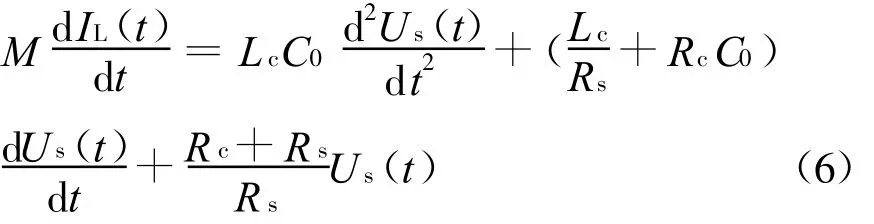
其傳輸函數為

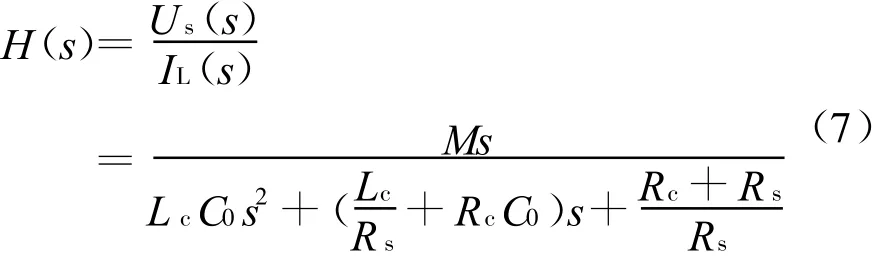
根據式(7)求得其下截止頻率和上截止頻率分別為

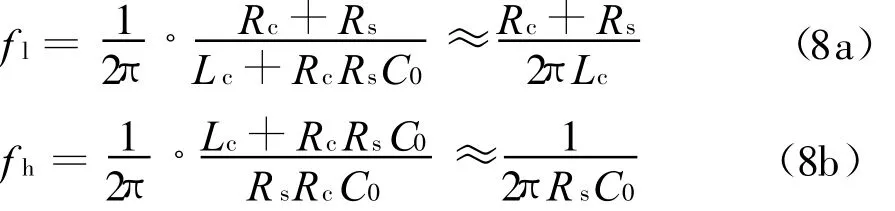
在計算線圈的諧振頻率時,將其等效為圖4所示電路。諧振時,有Im[Y(jω0)]=0,而

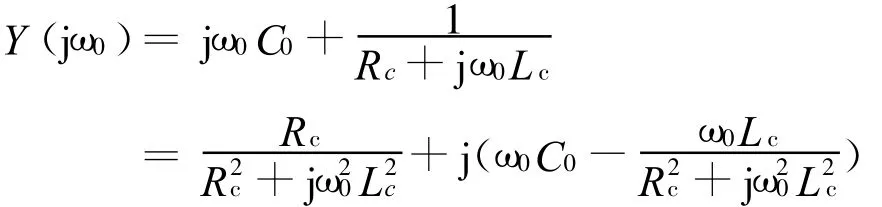
故有

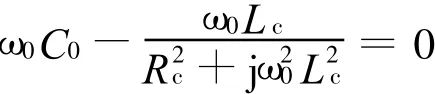
得諧振頻率為

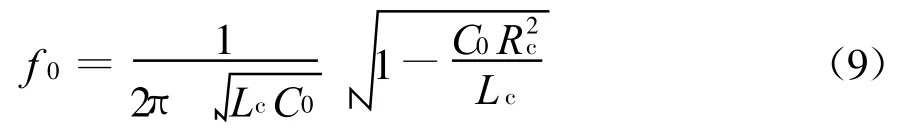
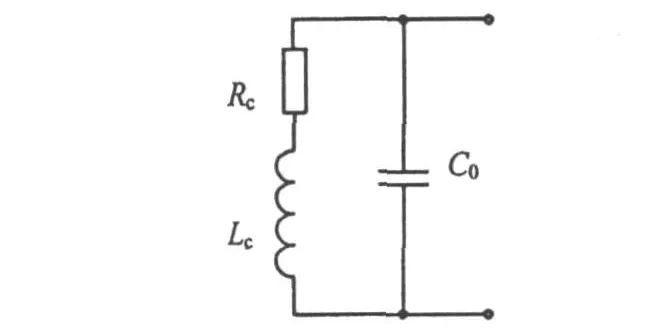
圖4 線圈諧振時的等效電路圖

3.1 分布電容的計算

為了防止外界雜散電場對線圈的耦合,需在線圈的外部加金屬屏蔽層。此時Rogowski線圈的分布電容C0主要為外層的金屬屏蔽層與繞制在柔性骨架上的線圈之間的電容。

圖5所示Rogowski線圈截面為圓形,設其骨架截面半徑為a,漆包銅線緊貼骨架纏繞;外屏蔽層橫截面半徑為b;線圈半徑為r。因為r?a、b,所以在計算分布電容C0時,可將其等效看作一個長度為2πr同軸型電容器,C0可按下式計算[8-9]

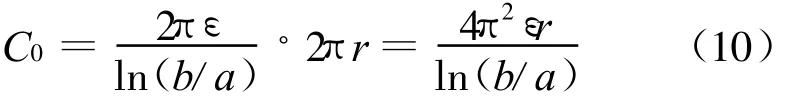
而實際線圈漆包銅線纏繞在圓形骨架上,在建模計算時將其近似為直的圓柱形導體,相當于增大了電容器兩極板之間的正對面積,所以真實電容值比計算值要小得多。本實驗中,線圈半徑 r為0.25 m,骨架截面半徑a為2.2 cm,屏蔽層橫截面半徑b為2.3 cm,計算出的電容值為1.9 nF。

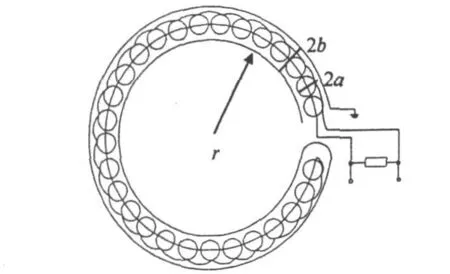
圖5 Rogowski線圈結構示意圖

4.實驗分析研究

本實驗所用的Rogowski線圈匝數為4000圈,計算出線圈的電感為

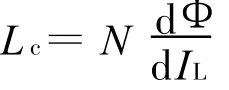
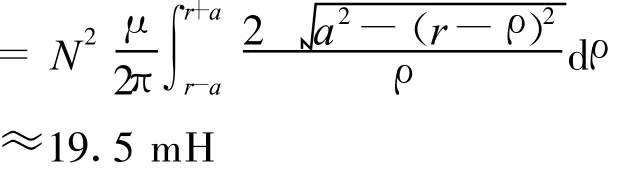
線圈實測的電感值約為23 mH,內阻R c為48 Ω,采樣電阻Rs選用標稱阻值為0.1Ω、功率為3 W的無感電阻[6]。

實驗裝置如圖6所示,脈沖電流流過脈沖磁場模擬器的圓環,Rogowski線圈套在這個圓環上,所采集的電壓信號由光發射機轉變光信號經光纖傳輸至光接收機,再轉變為電信號由示波器記錄顯示。在本實驗中考慮了兩種情況:一是線圈外加屏蔽層,即存在分布電容C0的情況;另外一種是不加屏蔽層,即去除C0這一影響因素。

圖6 實驗裝置實物圖

圖7 是加屏蔽層和不加屏蔽層兩種情況下Rogowski線圈的輸出波形,從實驗結果可以看出,加屏蔽層之后,由于分布電容C0的存在,線圈輸出波形上疊加了高頻振蕩;而去掉屏蔽層后,振蕩現象基本上消失。由式(9)計算出的振蕩頻率約為24 k Hz,而圖7顯示的振蕩頻率為70 k Hz,二者差距較大。這是因為計算分布電容時,將線圈視為為圓柱體,使電容C0的計算結果偏大,應加一個系數k加以修正,當k取為 0.2時,計算出的振蕩頻率為61 k Hz,與實驗結果就比較接近了。

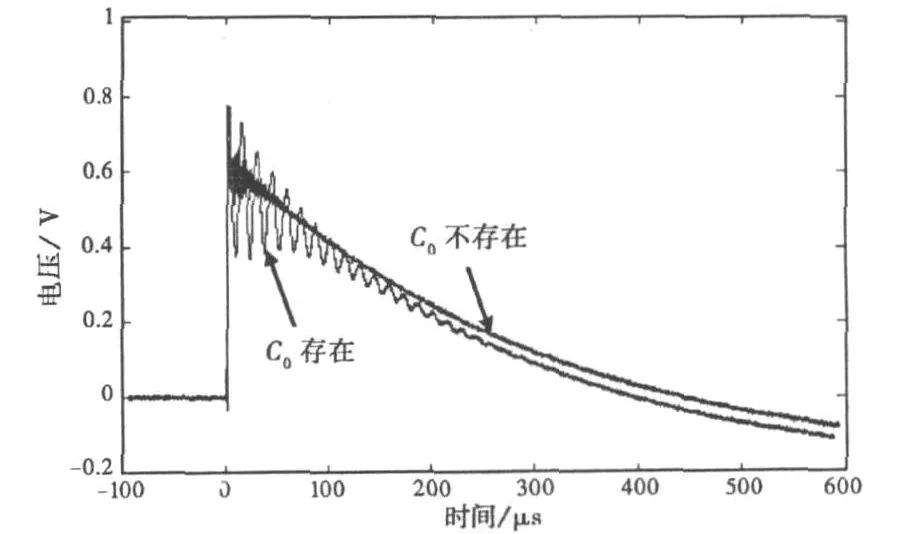
圖7 分布電容對線圈測量結果的影響

為了進一步證明減小分布電容C0能夠減小輸出波形的振蕩,在線匝外層套上熱縮管和纏繞管后再貼上屏蔽層,使外部屏蔽層與內部線匝之間的距離增大,從而達到減小分布電容的目的。實驗結果如下圖8所示。由圖8可見,當屏蔽層與內部線匝之間的距離很小時,輸出波形前沿出現明顯的振蕩(圖8中波形1);當屏蔽層與線匝間的距離增大后,輸出波形前沿的振蕩幅度明顯減小(圖8中波形2)。這不僅證實了測量波形前沿出現的振蕩是由Rogowski線圈的分布電容引起的,而且為解決因線圈加屏蔽層出現振蕩的問題找到了可行的辦法。

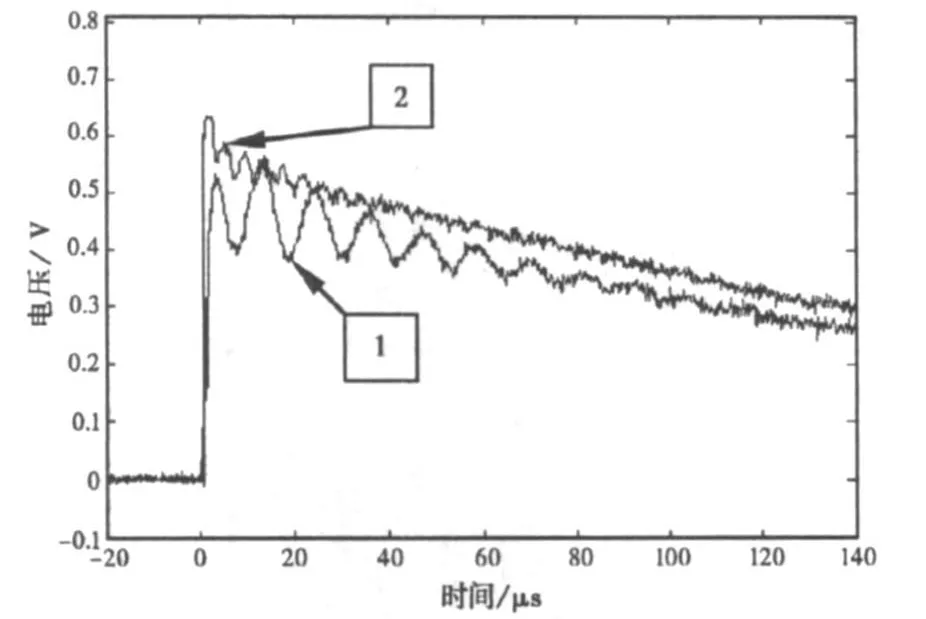
圖8 增大屏蔽層與線匝之間的距離對測量結果的影響

5.結 論

本文針對Rogow ski線圈外加屏蔽層后輸出波形出現的振蕩現象,建模進行了分析,說明了屏蔽所用的銅箔與線圈之間的分布電容是引起附加振蕩的主要因素。減小Rogowski線圈的分布電容,使附加振蕩的頻率提高至雷電流能量集中的頻帶以上,能有效減小線圈測量波形出現的附加振蕩。在Rogowski線圈屏蔽設計中,增大外屏蔽層與線圈之間的距離,以減小線圈的分布電容,可減小甚至避免測試波形上的振蕩現象。

[1] RAMBOZ JD.Machinable Rogowski coil,design,and calibration[J].IEEE Trans on Instrumentation and Measurement,1996,45(2):511-515.

[2] RAY W F,HEWSON C R.High performance Rogowski Current Transducers[C]//IEEE Industry Application Confer.Rome,Italy,2000,5:3083-3090.

[3] 楊 波,周璧華,石立華,等.雷電流測量專用柔性無磁芯大型Rogowski線圈[J].強激光與粒子束,2009,21(9):1421-1425.

YANG Bo,ZHOU Bihua,SHI Lihua,et al.Large Rogowski coil with flexible nonmagnetic core for lightning current measurement[J].High Power Laser and Particle Beams,2009,21(9):1421-1425.(in Chinese)

[4] 李維波.基于Rogowski線圈的大電流測量傳感理論研究與實踐[D].武漢:華中科技大學,2005.

LI Weibo.Study of sensor theory centered on Rogowski coil for heavy current measurement application[D].Wuhan:Huazhong University of Science and Technology,2005.(in Chinese)

[5] 李維波,毛承雄,陸繼明,等.分布電容對Rogowski線圈動態的影響研究[J].電工技術學報,2004,19(6):70-73.

LI Weibo,M AO Chengxiong,LU Jiming,et al.Study of influence of the distributed capacitance on dynamic property of Rogowski coil[J].Transactions of China Electrotechnical Society,2004,19(6):70-73.(in Chinese)

[6] 梁 瑜,蔣興良,楊 慶,等.雷電流測量用Rogowski線圈頻譜特性分析[J].高電壓技術,2005,31(5):18-20.

LIANG Yu,JIANG Xingliang,YANG Qing,et al.A-nalysis on the spectrum of Rogowski coil applied to measuring lightning current[J].High Voltage Engineering,2005,31(5):18-20.(in Chinese)

[7] 方 志,趙中原,邱毓昌,等.Rogowski線圈的高頻特性分析[J].高電壓技術,2002,28(8):17-18.

FANG Zhi,ZHAO Zhongyuan,QIU Yuchang,et al.Analysis on the High-frequency characteristics of Rogowski coil[J].High Voltage Engineering,2002,28(8):17-18.(in Chinese)

[8] ROBLESG,ARGIIESO M,SANZI J,et al.Identification of parameters in a Rogowski coil used for the measurement of partial discharges[C]//IEEE Instrumentation and Measurement Technology Conference.Warsaw,Poland,May 1-3,2007.

[9] GURU B S,HIZIROGLU H R.Electromagnetic Field Theory Fundamentals[M].2nd ed.Beijing:China Machine Press,2005.