戰場電磁信號環境最復雜原理預測

陳行勇 張殿宗 王 祎 肖昌達 陳海堅

(1.92493部隊博士后科研工作站,河北秦皇島066001;2.91404部隊,河北秦皇島066001)

1.引 言

戰場電磁信號環境定量分析是認識和理解戰場電磁環境本質規律的需要,可以為雷達信號分選和識別、戰場電磁環境構建、控制和評估提供技術支持。近年來,戰場電磁環境復雜度評估已經成為電子對抗領域的研究熱點[1-6]。作為系統科學新的分支,組成論[7]通過廣義集合、分布函數和復雜程度三個概念分析事物組成,為存在組成問題的客觀事物提供了統一的認識模型、分析工具、計算方法和原理,對于客觀事物的復雜程度給出了普遍的精確化定義,并揭示了有隨機性的事物都遵守最復雜原理[7]。組成論指出復雜程度如質量、能量一樣是客觀事物自身具有的客觀物理量,每個具體的客觀事物都有明確的復雜程度,這為復雜性研究提供了一條康莊大道。作為客觀事物,由于諧波分量、信號樣式和輻射源等都是由不同的因素組成,并且在時域、空域、頻域和能域的分布狀態存在差異,戰場電磁信號環境顯然存在組成問題,可以使用組成論的概念、模型和原理進行研究。至今未見將系統論的思想和方法應用于戰場電磁環境復雜性研究的報道。

雷達信號分選在雷達信號處理中占有很重要的作用[8-9]。國內有研究人員將熵的概念用于信號分選、聚類和識別[10-12],但是利用熵和復雜程度的概念進行戰場電磁環境定量分析很少。例如,文獻[13]認為脈沖密度不是電磁信號環境復雜程度合適的度量值,引入類型熵和密度熵作為電磁環境復雜性測度,探討了電磁信號環境熵度量。文獻[14]針對跳頻信號的偵察、分選,提出了“復合信息熵”的定量評估指標,該指標綜合考慮電磁環境中的信號類型數、跳頻信號數目、跳速和信道分布情況。

現代戰場電磁輻射源的多元化是電磁環境復雜化的根本原因。電磁環境的復雜性表現在電磁波傳播在空域上的交錯、電磁輻射行為在時域上的集中、電磁輻射信號載頻在頻域上的擁擠和電磁輻射強度在能域上的起伏。每一域的電磁輻射活動情況都分別從不同方面表現出電磁環境的復雜。由于電磁波的交叉傳播,才使得同一時間內,空間中的任一點上能夠同時接收到眾多信號,這些信號的頻譜分布具有足夠的隨機性,同時戰場電磁兼容又為這種隨機性提供了限制條件。這為使用最復雜原理分析其頻譜分布規律提供了理論依據。

利用組成論分析戰場電磁信號的組成,通過定義電磁信號時間、頻譜和空間分布狀態的復雜程度,在戰場電磁信號環境具有足夠的隨機性的條件下,利用最復雜原理和戰場電磁兼容的約束條件,預測電磁信號頻譜寬度分布規律,并進行了仿真計算。

2.戰場電磁信號環境頻譜分布預測

2.1 復雜程度的概念

根據組成論,對于一個廣義集合[7],由于其個體總個數N是確定值,而標志值為x的個體個數n是x的函數,所以n/N也是x的函數,則廣義集合的內部狀態的離散變量復雜程度為

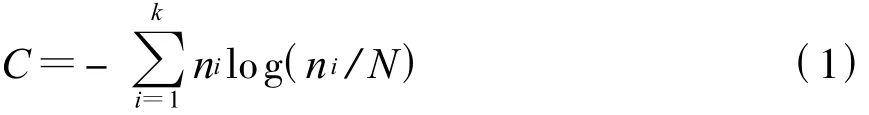
式中:k表示廣義集合內的不同的標志值的個數;ni表示每種標志值占有的個體的數量。

設g(x)表示廣義集合的密度分布函數,f(x)表示相對密度分布函數,即標志值 x有單位增量時個體個數的增量。則廣義集合的內部狀態的連續變量復雜程度為

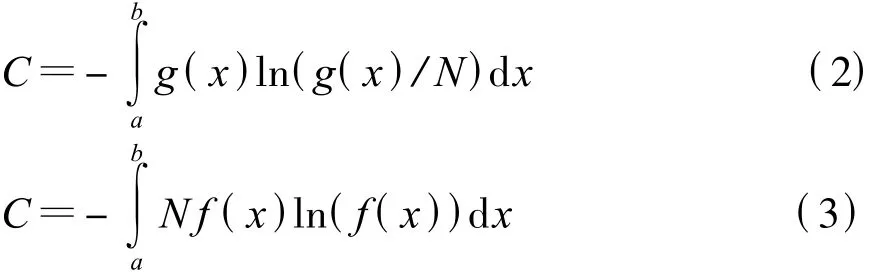
組成論指出,一個廣義集合內的各個個體的特征(標志值)差別越大,復雜程度值C就越大。而各個個體的特征(標志值)完全相同(清一色,沒有差別)則C為零。復雜程度是廣義集合分布函數的泛函數。客觀事物都有復雜程度值,且復雜程度沒有負值。

2.2 電磁信號環境復雜程度

將戰場電磁信號全體視為一廣義集合,各電磁信號在時間持續長度、頻譜占用寬度和空間體積大小方面存在差異,因此,按照組成論,戰場電磁信號環境具有明確的復雜程度量。設在時間[t1,t2]內,頻率[f 1,f 2]內,空間VΩ內,戰場電磁信號源總數為N。戰場電磁信號關于時間寬度t的相對分布函數為st(t),st(t)即為時間占有寬度為t的戰場電磁信號占信號總數的比例;戰場電磁信號關于頻譜寬度f的相對分布函數為s f(f),sf(f)即為頻譜寬度為f的戰場電磁信號占信號總數的比例;可以被感知的戰場電磁信號關于空間體積v的相對分布函數為(v),(v)即為占有空間體積為v的戰場電磁信號占信號總數的比例。

2.2.1 時間寬度分布復雜程度

定義戰場電磁信號環境的時間寬度分布復雜程度為

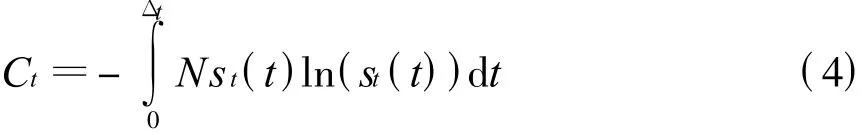
2.2.2 空間體積分布復雜程度

定義戰場電磁信號環境的空間體積分布復雜程度為

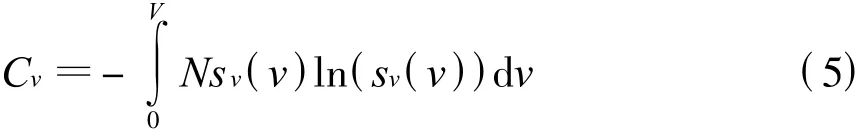
式中:V為戰場空間體積;Cv描述了戰場電磁信號環境關于占有空間體積大小差異的豐富程度。

2.2.3 頻譜寬度分布復雜程度

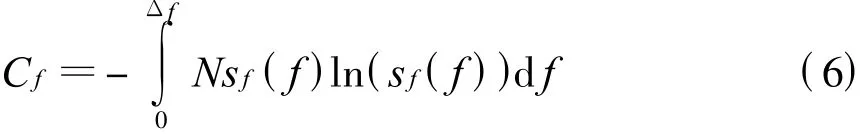
定義戰場電磁信號環境的頻譜寬度分布復雜程度為式中,Δf=f2-f1。Cf描述了戰場電磁信號環境關于頻譜寬度差異的豐富程度。

2.3 基于最復雜原理的頻譜寬度分布函數預測

2.3.1 戰場電磁頻譜分割

由于每個廣義集合都有一個明確的分布函數,尋找和獲得分布函數就意味著發現了一類現象背后隱藏的規律,所以,每當把某些客觀事物歸結為廣義集合以后的一個重要目標就是找出該廣義集合的分布函數。對于有隨機性的廣義集合,由于它服從最復雜原理,這就提出了一個新的普遍適用的思路:利用最復雜原理從理論上求解廣義集合的分布函數。由于復雜程度是分布函數的泛函數,因此可以利用復雜程度(泛函數)最大,加上一定的約束條件,求得廣義集合的分布函數。

戰場電磁信號占有頻譜寬度分布可以抽象為“斬亂麻”[7]問題。戰場電磁兼容要求在同一戰場電磁環境下,己方各種作戰裝備能夠執行各自的作戰功能,并且不降低戰技指標。在同一戰場電磁環境下的作戰裝備包括雙方的作戰裝備,戰場電磁兼容往往是針對作戰的己方而言的,作戰雙方的電磁兼容是絕對不可能實現的。從電子對抗方面來說,作戰時一方的目標,就是最大限度地讓己方的干擾設備與對方的信息化裝備不兼容。對于己方接收的對方電磁信號來說,戰場電磁兼容的要求使得電磁信號的頻譜具有不交叉分割占用的最大可能性,換一句話說,若接收到的對方電磁信號對頻譜的分割占用具有足夠的隨機性,頻譜寬度的長短就構成了其復雜性,則依據最復雜原理,電磁信號的頻譜寬度分布狀態具有最復雜的趨勢。因此戰場電磁信號對頻譜的分割占用問題就是把戰場電磁信號看成一個廣義集合而尋找它關于頻譜寬度的分布函數。

2.3.2 頻譜寬度分布預測

在頻譜寬度 f為連續變量的情況下,戰場電磁信號頻譜寬度的相對分布函數為sf(f)的含義是頻譜寬度在 f到f+δf很小范圍(δf為f的微元)的信號源占信號源總數N的百分比為sf(f)·δf,而它的復雜程度Cf應當是

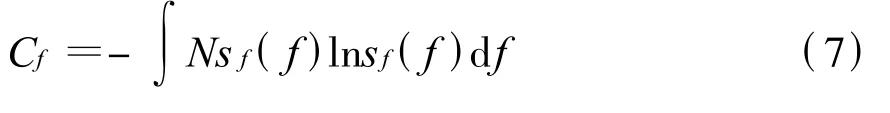
式(7)表明復雜程度Cf是分布函數sf(f)的泛函,其最大值以及取最大值時的sf(f)可以利用拉格朗日方法求解。使用拉格朗日方法求解這個未知函數還要約束條件,頻譜寬度之和一定提供了這個約束條件。所謂頻譜占用就是把頻譜分割成很多段,假設各信號頻譜寬度的合計值等于 μΔf,若0≤μ＜1,則信號源必定存在未占用的頻段,若μ＞1,則信號源必定存在共同占用的頻段,若μ=1,則頻譜恰好被無縫無交叉占用,或者未占用和共同占用的頻段同時存在。根據分布函數的含義,顯然有

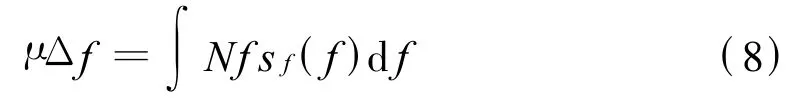
即信號源集合的頻譜寬度之和是各個信號源頻段寬度與其占的百分比的乘積再乘以信號源總數N的積分。而各個信號源的百分比(sf(f)Δf)的積分(合計值)顯然應當等于100%,即

式(8)和式(9)分別表示兩個約束條件,其含義是各個信號源頻譜寬度的總和與信號源頻譜范圍寬度的μ倍相等,各個信號源的數量的合計值與總的信號源數量相等。由拉格朗日法可知,求分布函數sf(f)需構造一個新的函數F

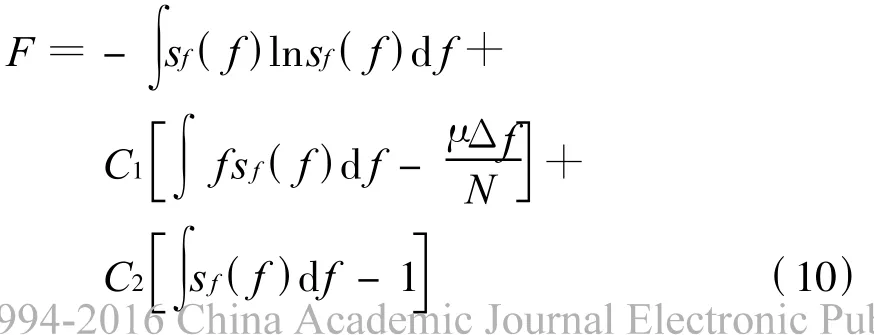
式中,C1和 C2是與 Δf,N,μ有關的常數。對式(10)求解,得到使復雜程度極大對應的分布函數為

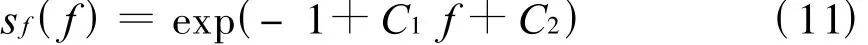
利用式(8)和(9)與式(11)聯立可以消去未知常數 C1,C2。解得

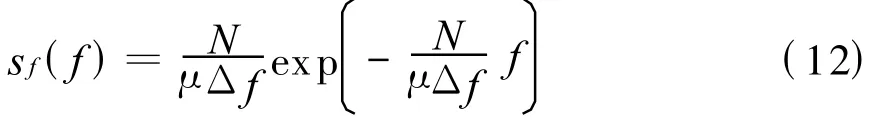
注意到μΔf/N的含義是信號源頻譜的平均寬度,以w 表示它,得到

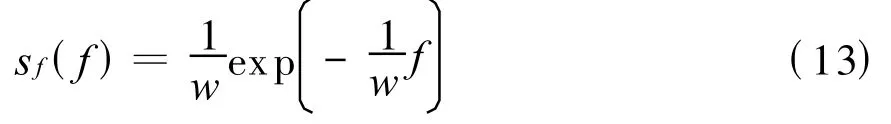
它是一個負指數分布函數。它顯示頻譜寬度 f窄的信號源多而頻譜寬的信號源的數量依負指數關系而減少。

3.仿真計算和結果分析

3.1 仿真計算

假設有一段范圍為[f 1,f 2],寬為Δf=f 2-f 1的頻譜被足夠多的N個戰場電磁輻射源隨機占有,并且假設對于0≤μ＜1,對應信號源有未占用的頻段且無共同占用頻段,對于μ＞1,對應信號源無未占用的頻段且有共同占用頻段,對于μ=1,對應頻譜恰好被無縫無交叉占用,可以采用以下方法對電磁信號頻譜寬度分布進行模擬。

1)在[0,1]范圍內產生N-1個均勻分布隨機數并乘以Δf后加f 1,與f 1和f 2一起由小到大構成一個N+1點序列x(m),x(m)服從[f 1,f 2]上的均勻分布,它們即是頻譜占用的斷點;

2)計算序列 x(m)的相鄰數值的差,并乘以μ,得到的就是各個戰場電磁輻射源占用的頻譜寬度;

3)統計這些頻譜寬度的分布,即統計分布在各個頻譜寬度區間的輻射信號的數量占總數的百分比,得到戰場電磁信號頻譜寬度分布函數;

4)把統計得到的信號頻譜寬度分布與理論預測進行比較,即將統計分布與預測得到的分布函數sf(f)=(1/w)·exp(-f/w)進行對比。

3.2 結果分析

取Δf=f 1=10 MHz,f 2=20 MHz,N=1000,圖1示出了 μ=1,μ=1.2和 μ=0.8時實驗得到的戰場電磁信號頻譜寬度分布與理論預測的對比。

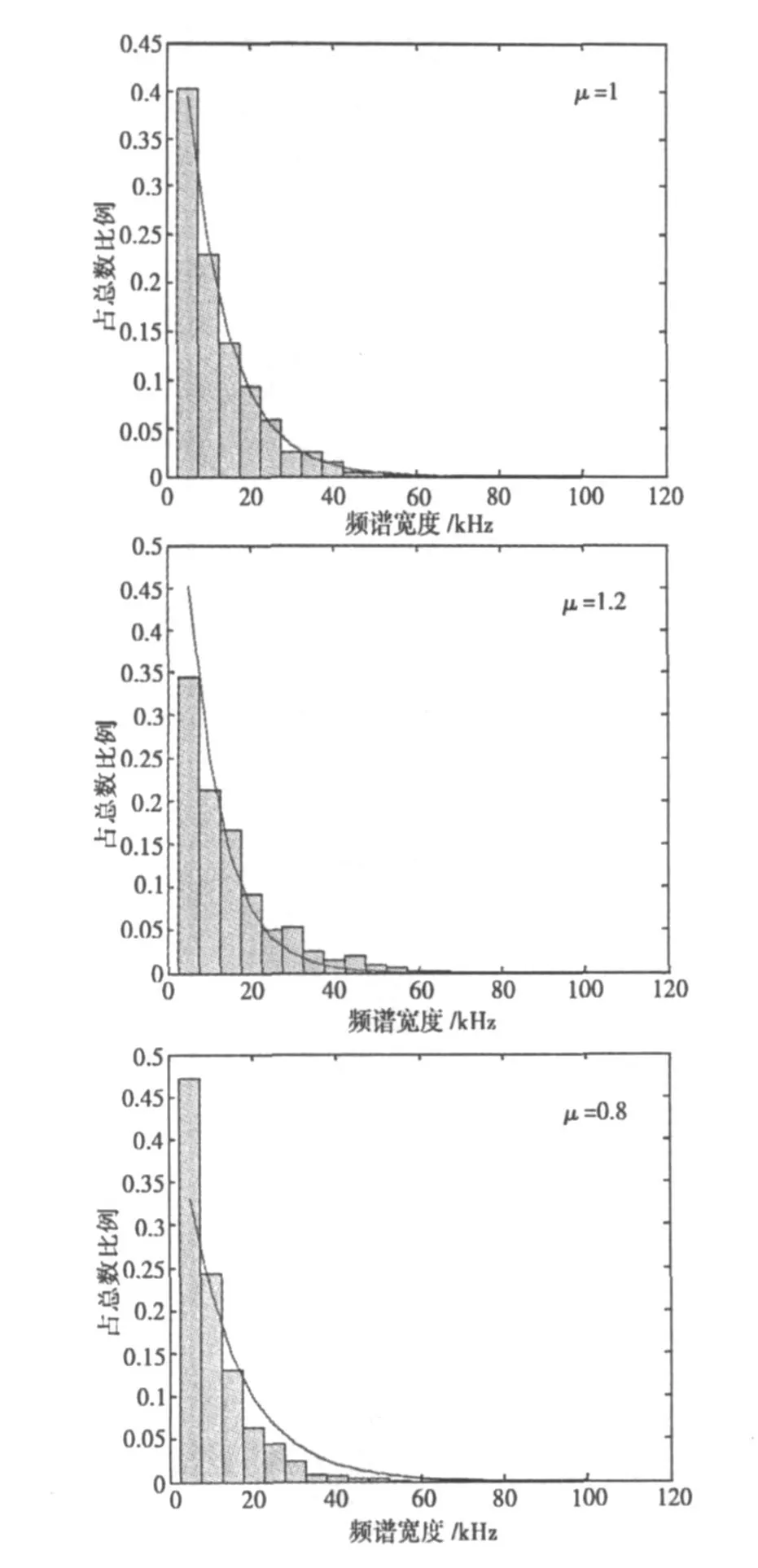
圖1 戰場電磁信號頻譜寬度分布仿真與理論預測的對比

由圖1可知,計算機模擬數據和理論計算吻合。戰場電磁信號的數量隨著其占有的頻譜的寬度增加急劇減小,其變化規律服從負指數分布。這為我們理論預測戰場電磁信號環境的頻譜和帶寬分布提供了理論依據,可以指導我們構建電子對抗訓練復雜電磁環境,也可以為雷達信號分選、聚類、識別提供新的途徑。

4.結 論

熵和復雜程度是信息論和系統科學的重要概念,然而熵原理(最復雜原理)在電子對抗領域卻沒有發揮應有的作用,這是我們應該重視的問題。從戰場電磁信號環境的時間、空間和頻率占用的差異來定義復雜程度,用最復雜原理預測戰場電磁信號頻譜寬度分布函數,不僅為客觀定量分析戰場電磁環境復雜性提供了新的途徑,而且為復雜戰場電磁環境下雷達、通信信號分選、聚類和識別提供了新的思路。本文既是熵與交叉科學研究的探索,也是為將熵原理推廣到戰場電磁環境分析所進行的初步嘗試。

[1] CAI X F,SONG JS.Analysis of complexity in battlefield electromagnetic environment[C]//IEEE Conference on Industrial Electronics and Applications.Xi'An:IEEE,2009:2440-2442.

[2] JAEKEL B W.Electromagnetic environments-Phenomena,classification,compatibility and immunity levels[C]//Proceedings of The IEEE Region 8 Conference.St.Petersburg,Russia:IEEE,2009:1498-1502.

[3] XU J H,LIU G B,YU Z Y,et al.A meta-synthesis of evaluating battlefield electromagnetic environment effects[C]//International Conference on System Simulation and Scientific Computing.ChengDou:IEEE,2008:79-82.

[4] 陳行勇,張殿宗,王 祎,等.面向對象的戰場電磁環境復雜度評估[J].電子對抗信息技術,2010,25(2):74-78.

CHEN Hangyong,ZHANG Dianzong,WANG Yi,et al.Object-oriented battlefield electromagnetic environment complexity evaluation[J].Electronic Information Warfare Technology,2010,25(2):74-78.(in Chinese)

[5] 代合鵬,蘇東林.電磁環境復雜度定量分析方法研究[J].微波學報,2009,25(3):25-27.

DAI Hepeng,SU Donglin.Study of the complexity evaluation on electromagnetism environment[J].Journal of Microwaves,2009,25(3):25-27.(in Chinese)

[6] 邵國培,劉雅奇,何 俊.戰場電磁環境的定量描述、模擬構建與復雜性評估[C]//中國電子學會電子對抗分會第十六屆學術年會論文集.貴陽:中國電子學會電子對抗分會,2009:61-66.

[7] 張學文.組成論[M].合肥:中國科學技術大學出版社,2004:1-6.

[8] 朱 明,普運偉,金煒東,等.基于時頻原子方法的雷達輻射源信號特征提取[J].電波科學學報,2007,22(3):458-462.

ZHU Ming,PU Yunwei,JIN Weidong,et al.Feature extraction of radar emitter signals based on time frequency atoms[J].Chinese Journal of Radio Science,2007,22(3):458-462.(in Chinese)

[9] 陶榮輝,李合生,韓 宇,等.基于直方圖和小波網絡的雷達信號識別方法[J].電波科學學報,2005,20(6):784-788.

TAO Ronghui,LI Hesheng,HAN Yu,et al.A novel algorithm of radar signal recognition based on histogram and wavelet networks[J].Chinese Journal of Radio Science,2005,20(6):784-788.(in Chinese)

[10] 孫盼杰,劉 剛,王 杰.基于PRI熵的雷達信號聚類方法研究[J].電子信息對抗技術,2008,23(1):22-25.

SUN Panjie,LIU Gang,WANG Jie.Approach to radar signal clustering based on PRI entropy[J].Eelectronic Information Warfare Technology,2008,23(1):22-25.(in Chinese)

[11] 張葛祥,胡來招,金煒東.基于熵特征的雷達輻射源信號識別[J].電波科學學報,2005,20(4):440-445.

ZHANG Gexiang,HU Laizhao,JIN Weidong.Radar emitter signal recognition based on entropy features[J].Chinese Journal of Radio Science,2005,20(4):440-445.(in Chinese)

[12] 國 強.復雜環境下未知雷達輻射源信號分選的理論研究[D].哈爾濱:哈爾濱工程大學,2007.

GUO Qiang.Intelligent recognition methods for radar emitter mignals[D].Harbin:Harbin Engineering U-niversity,2007.

[13] 李 崢.電磁信號環境的熵度量第十三屆電子戰新概念新理論新技術學術年會論文集[C]//成都:電子對抗國防科技重點實驗室,2009:204-208.

[14] 陳利虎,張爾揚.一種新的定量評估電磁環境復雜度方法[J].電子對抗,2009,33(2):6-9.

CHEN Lihu,ZHANG Eryang.A new method for the quantificational evaluation of the complexity of electromagnetic environment[J].Electronic Warfare,2009,33(2):6-9.(in Chinese)