全站儀三角高程測(cè)量?jī)煞N方法精度淺析

王百勇

在工程測(cè)量中,高程控制是各種工程高程施工放樣的基礎(chǔ)。傳統(tǒng)的高程控制的測(cè)量方法是幾何水準(zhǔn)測(cè)量和三角高程測(cè)量。水準(zhǔn)測(cè)量直接測(cè)得地面兩點(diǎn)間高差,操作簡(jiǎn)單,測(cè)量精度也高,但受地形的限制;三角高程測(cè)量是一種間接測(cè)得兩點(diǎn)高程的方法,它不受地形條件的限制,且測(cè)量速度快,但精度較低。因此,有研究者提出一種全站儀三角高程測(cè)量的新方法。即將全站儀安置在兩測(cè)點(diǎn)中間,在不量取儀器高和棱鏡高的情況下,利用三角高程的原理測(cè)得未知點(diǎn)的高程,然而此方法誤差隨觀測(cè)距離和豎直角的增大而增加。上述三種方法雖各有優(yōu)缺點(diǎn),但適用于不同的范圍,下面從三角高程測(cè)量原理出發(fā),利用誤差傳播定律,對(duì)這兩種三角高程測(cè)定方法進(jìn)行精度分析。

1 全站儀安置于已知點(diǎn)的三角高程中誤差

1.1 觀測(cè)原理

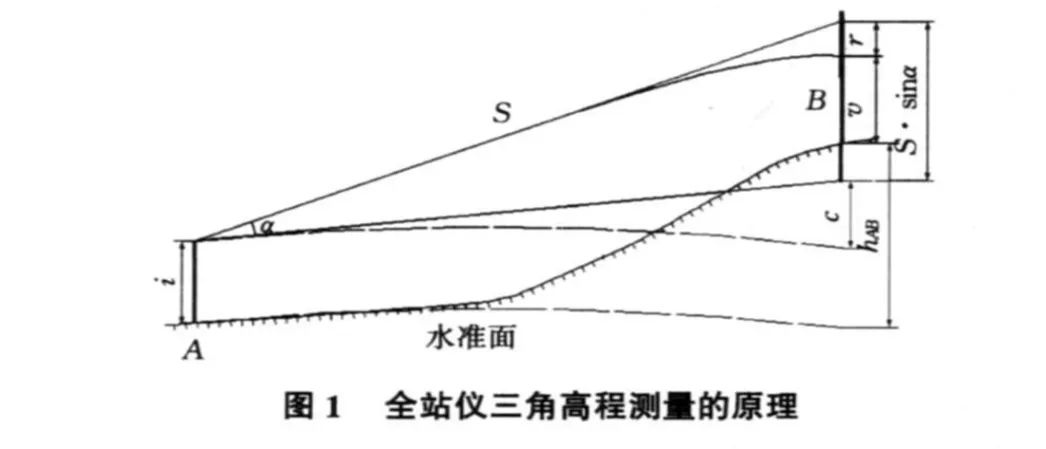
全站儀單向三角高程測(cè)量如圖1所示,其中A為高程已知點(diǎn),B為待測(cè)高程點(diǎn),將全站儀安置于A點(diǎn),量取儀高為i,將棱鏡置于B點(diǎn),量得棱鏡高為v。由圖1可得A,B兩點(diǎn)間的高差計(jì)算公式為:

其中,hAB為A,B兩點(diǎn)的高差;S為斜距;α為豎直角;c為地球曲率改正數(shù);r為大氣折光系數(shù)改正數(shù)。

在用全站儀進(jìn)行三角高程測(cè)量時(shí),一般進(jìn)行對(duì)向觀測(cè),即往返測(cè)。如果在相同的觀測(cè)條件下進(jìn)行,則可認(rèn)為大氣折光系數(shù)對(duì)于反向觀測(cè)基本相同,即K往≈K返。所以可得出對(duì)向觀測(cè)時(shí)三角高程計(jì)算高差的基本公式為:

1.2 精度分析

其中,mh為往返測(cè)量的平均高差中誤差;ms往,ms返為往返距離中誤差;mα往,mα返為往返豎直角中誤差;mi往,mi返,mv往,mv返為往返儀器高和棱鏡高中誤差。

又由于儀器和觀測(cè)條件相同,所以可以認(rèn)為:ms往=ms返=ms,mα往=mα返=mα,再令S往=S返=S,mi往=mi返=mv往=mv返=m,同時(shí)α往,α返相差不大,也可以認(rèn)為近似相等,即 α往=α返=α,則平均高差的中誤差關(guān)系式可簡(jiǎn)化為:

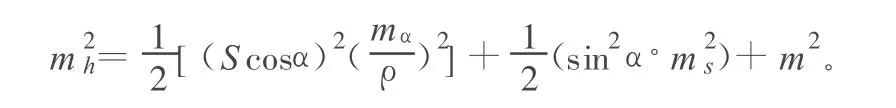
2 全站儀安置于兩點(diǎn)之間的三角高程中誤差

2.1 觀測(cè)原理

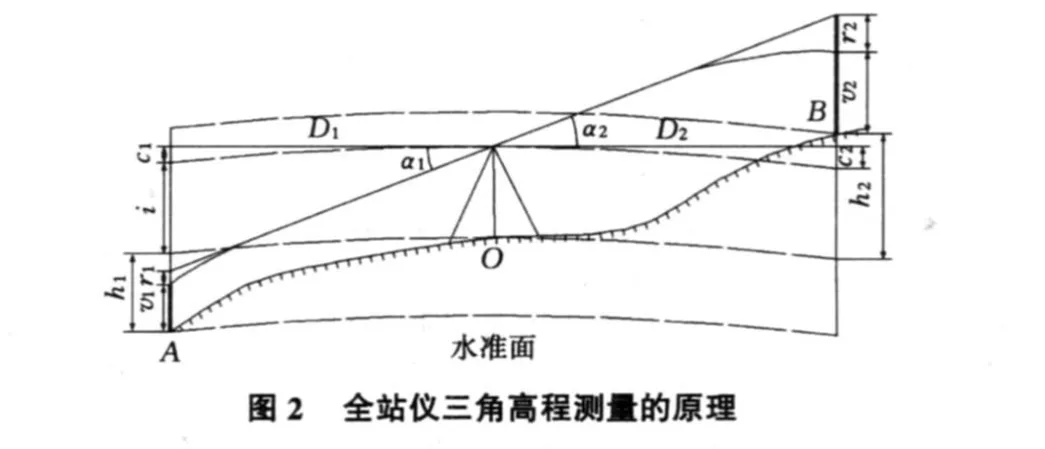
如圖2所示,在已知點(diǎn)A和未知點(diǎn)B分別安置棱鏡,在AB中間安置全站儀,根據(jù)三角高程觀測(cè)原理,可知A,B兩點(diǎn)的高差為:hAB=hOB-hOA=(S2·sinα2-S1·sinα1)+(c2-r2)-(c1-r1)-(v2-v1)。采用中點(diǎn)法測(cè)量高差時(shí)使A,B兩點(diǎn)鏡高相等,即v2=v1,將球氣差的公式代入得到:

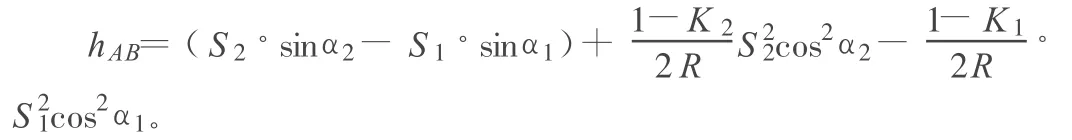
由此式可以看出,全站儀中點(diǎn)法高程測(cè)量只與斜距、豎直角和大氣折光系數(shù)有關(guān)。

2.2 精度分析

根據(jù)誤差傳播定律,對(duì)上式進(jìn)行微分,并變?yōu)橹姓`差關(guān)系式,考慮到在千米以下的高程測(cè)量中,球氣差很小,可忽略不計(jì)。再用平距代替斜距,即D=S·cosα,則得到:

其中,mk1,mk2分別為O點(diǎn)至A點(diǎn)和B點(diǎn)的大氣折光系數(shù)中誤差;R為地球曲率半徑,R=6 371 km,后兩項(xiàng)對(duì)高差的影響很小,可以忽略不計(jì)。

若再使前后平距、大氣折光系數(shù)近似相等,前后豎直角也盡量接近相等,則公式變?yōu)?

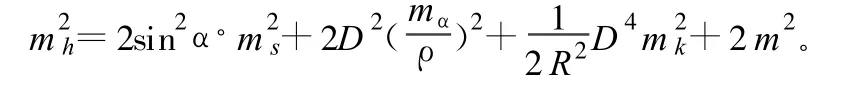
其中,m為棱鏡高量取中誤差;mk為大氣折光系數(shù)中誤差。

3 兩種方法的精度比較

為了對(duì)全站儀三角高程測(cè)量的精度進(jìn)行更好的分析,利用前面所推導(dǎo)的中誤差公式,對(duì)不同的測(cè)量距離,不同的豎直角進(jìn)行精度估算,并取2倍的中誤差作為極限誤差。以工程中常用的J2全站儀為例,取mα=±2″,測(cè)距標(biāo)稱精度為±(2 mm±2 ppm×D)。測(cè)距按1 km計(jì)算,取ms=±4 mm,mk=±0.04 mm,儀器高與棱鏡高的量取誤差m=±2 mm。

通過比較可以看出,對(duì)向觀測(cè)高程測(cè)量精度比中點(diǎn)法精度要好。對(duì)向觀測(cè)高程測(cè)量在距離小于1 200 m,豎直角小于30°時(shí),其精度能滿足四等水準(zhǔn)的精度要求;當(dāng)距離大于200 m且小于600 m,豎直角小于30°時(shí),對(duì)向觀測(cè)可滿足三等水準(zhǔn)測(cè)量的精度要求。

4 結(jié)語

在適當(dāng)?shù)木嚯x及豎直角范圍內(nèi),可以用全站儀三角高程測(cè)量方法代替水準(zhǔn)測(cè)量方法,提高了測(cè)量速度,節(jié)省了外業(yè)作業(yè)時(shí)間。

[1]何習(xí)平.全站儀中間法與水準(zhǔn)測(cè)量的精度比較[J].水電自動(dòng)化與大壩監(jiān)測(cè),2004,28(4):37-39.

[2]張智韜.全站儀三角高程測(cè)量方法及精度分析[J].西北農(nóng)林科技大學(xué)學(xué)報(bào),2008,36(9):229-234.

[3]孔祥元,梅是義.控制測(cè)量學(xué)[M].武漢:武漢大學(xué)出版社,2002:270-279.