高職建筑力學課程教學改革探討

孫琴琴

0 引言

《建筑力學》是土木工程專業的一門重要專業基礎課,但處于教學一線的教師普遍感到當前的高職學生學習該課程的興趣不高,課堂重視度不夠,力學課相當難教。頭疼當前學生“一上力學課就睡覺”的現狀,但苦于改革無從著手。本文將以一堂典型的建筑力學課為案例,提出一系列提高《建筑力學》課教學效率的有效措施。

1 案例

1.1 課題

靜定梁的受力圖。

1.2 教學目標

能夠熟練繪制靜定梁的內力圖;會利用技巧校核結果的正確性;會判斷梁上危險點的位置;能夠總結規律,利用規律。

1.3 教學重點

按步驟繪制內力圖(求關鍵點的內力);判斷梁上危險點的位置。

1.4 教學難點

均布荷載作用的梁段上,剪力為0時,彎矩極值的求解。

1.5 教學步驟

1)基礎知識回顧,展示建筑物圖片,說明本節課的課程目標及重難點。

2)講解例題。試做出如圖1所示的簡支梁的剪力圖和彎矩圖。

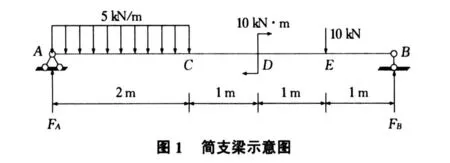
a.求得支座反力為:

FA=16 kN,FB=24 kN。

b.將梁分為 AC,CD,DE,EB四段(課堂提問:分段依據)。

c.做剪力圖(見圖2)。

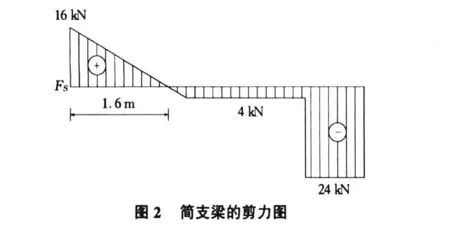
d.繼而做彎矩圖。

求 C截面(關鍵點 C)處的內力彎矩 MC,畫出隔離體圖如圖3所示。

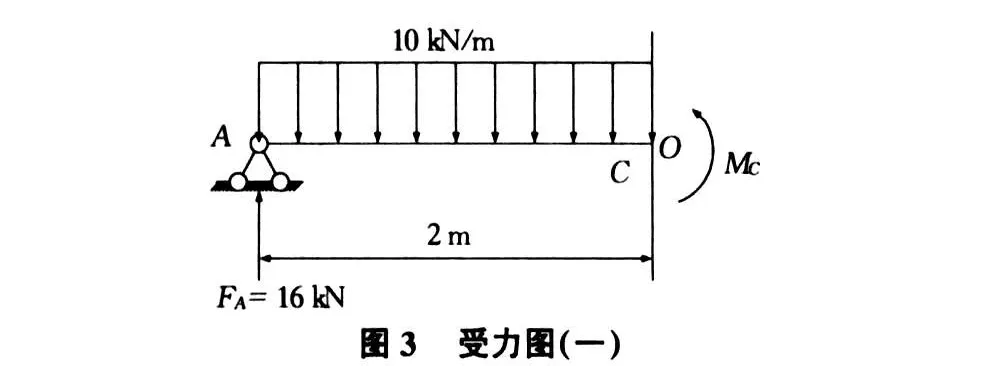
列平衡方程:

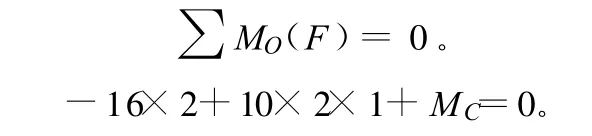
可得:MC=12 kN·m。

同理,求得 D,E截面(關鍵點D,E)左臨右臨彎矩。

特別地(教學難點),在均布荷載梁段,剪力為0處,即 x=1.6 m處(G點),彎矩圖出現最大值Mmax,取隔離體如圖4所示。

列平衡方程:

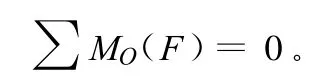
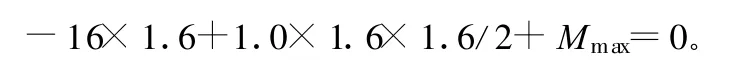
可得:Mmax=12.8 kN·m。

綜上所述,繪制梁的彎矩圖如圖5所示。

e.判斷梁上危險點(D,E)。

3)啟發學生總結規律。

a.在無荷載作用的一段梁上,該梁段內各橫截面的剪力FS(x)為常數,故剪力圖必為平行于 x軸的直線;如 CD,DE,EB段;彎矩圖必為斜直線,且斜直線的斜率等于該梁段的剪力。并驗證:

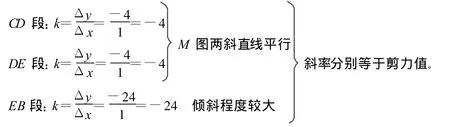
b.在均布荷載作用的一段梁上,q(x)為常數,剪力圖必然是斜直線,如 AC段,斜率為集度 q的大小(驗證-10),彎矩圖是二次拋物線。若某截面上的剪力FS(x)=0,則該截面上的彎矩必為極值。當x=1.6 m時,剪力為0,彎矩有極值 M1.6=12.8 kN·m。

c.在集中力作用處的左右兩側截面上剪力圖發生突變,突變值等于集中力的數值,如E點。兩側截面上的彎矩值相等,但是由于兩側的剪力值不同,所以彎矩在集中力作用處兩側的斜率不相同,彎矩圖發生轉折,出現尖角,尖角的指向與集中力的指向相同。

d.集中力偶作用的左右兩側截面上,剪力相等;彎矩發生突變,突變值等于集中力偶的數值(如D點)。

4)課后習題當堂練,熟能生巧。

2 結語

以上一堂看似傳統的教學卻處處閃爍著改革的光芒:

1)前3 min提問(繪制梁的內力圖有哪些基本規定)以及教學過程中提問(分段依據)有助于學生溫故知新,前后知識銜接,從而在頭腦中形成力學體系;2)求彎矩最大值 Mmax的過程中,避開教科書上學生不熟練的積分法,轉而利用已有知識(取相應隔離體,列平衡方程),條條道路通羅馬,增強學生成就感;3)教具展示(建筑圖片),使抽象、理論、晦澀的問題具體、實踐、活潑化,啟發學生帶著疑問、帶著問題有目的聽課,以此來調動學生的積極性、主動性;4)注重基本技能的培養[2]:截面法作梁的內力圖這種技能通過例題講解習題反復操練,必須掌握;5)鼓勵學生總結規律并利用,增強學生教學參與程度。

[1] 顧華詳.論科學發展觀視野下的高職教育發展戰略[J].烏魯木齊職業大學學報(人文社會科學版),2007(1):26-27.

[2] 陳燕菲,李 英.探索建筑工程專業課程設計的一體化模式[J].貴陽金筑大學學報,2002(1):100-103.