點擊概率問題求解時的常見錯誤

●張禹水 (鄞州中學 浙江寧波 315000)

概率知識是高中數學新課程新增加的內容，也是排列、組合知識的應用及延伸.學生在學習過程中普遍感覺概率問題比較抽象、難以理解.在解題過程中也往往會因為概念理解不透、審題不嚴、考慮不周或忽視公式成立的條件等等而出現錯誤.為此，筆者對概率問題中學生易犯的錯誤作如下歸納總結，供讀者借鑒與參考.

類型1 “等可能”與“非等可能”概念混同

例1 將一枚骰子連續拋擲2次，所得點數之和等于5的概率是多少?

剖析將一枚骰子連續拋擲2次，有36種等可能事件：

例2 某人有5把鑰匙，其中有1把是辦公室的抽屜鑰匙，但他忘了是哪一把，于是他便將5把鑰匙逐把地不重復試開.問恰好第3次打開抽屜的概率是多少?

錯解5把依次逐把試開，相當于5把鑰匙在5個位置的全排列，即n=.“第3次打開”即是第3次已經打開，只需考慮第1次和第2次的情形，則 m=，所以

剖析由等可能事件的概率定義知：n為一次試驗中所包含的所有基本事件數，m為此試驗中事件A所包含的基本事件數.從集合的角度看：在一次試驗中，等可能出現n個結果組成一個集合U，這n個結果就是集合U的n個元素;包含m個結果的事件A對應于U的含有m個元素的子集A.因此事件A的概率是子集A的元素個數與集合U的元素個數的比值.在錯解中取n=，是把“5把鑰匙依次逐把打開”作為“一次試驗”，但取m=，是把事件A作為“第3次恰好打開情形下前3個位置的排列”，顯然前后兩者不是同一試驗類型.從集合角度看，此時A也不是U的子集，所以解答錯誤.正確解法如下：

5把鑰匙依次逐把試開，相當于5把鑰匙在5個位置的全排列，即n=，“恰好第3次打開”說明抽屜鑰匙固定在第3個位置，因此m=，所以

若強調“第3次恰好打開”的情形，則“一次試驗應確定為前3次試開中，抽屜鑰匙在第3個位置，得 n=A35，m=A24，所以

類型2 “有序”與“無序”概念混同

例3 甲、乙2人參加普法知識競賽，共有10道不同的題目，其中選擇題6道，判斷題4道，甲、乙2人依次各抽取1道題.

(1)甲抽到選擇題、乙抽到判斷題的概率是多少?

(2)甲、乙2人至少有1人抽到選擇題的概率是多少?

(2)設甲、乙2人至少有1人抽到選擇題為事件A，則甲、乙2人都未抽到選擇題為事件.由對立事件的計算公式，得

剖析本題中把“12個停車位停8輛車”作為一次試驗，計算n時把停車方法按有序進行，即作為排列問題處理.而在計算m時僅考慮4個空位相連而沒有考慮8輛車的有序排放問題，即作為組合問題處理.由等可能事件概率意義知，前后兩者不是同一試驗類型，因此解答錯誤.正確解法如下：

要正確解決有關概率問題，必須充分理解概率的定義，在解題時要認真分析題意，確實把握n與m的意義，這樣才能正確解題.

類型3 “互斥事件”與“獨立事件”概念混同

例5 甲、乙、丙3名射手擊中目標的概率分別為0.7，0.8，0.85.若他們 3 個人分別向目標發射1槍，試求3彈都脫靶的概率.

錯解設甲發射1槍擊中目標為事件A，乙發射1槍擊中目標為事件B，丙發射1槍擊中目標為事件C，則甲、乙、丙3人分別向目標發射1槍擊中目標為事件ABC，從而甲、乙、丙3人分別向目標發射1槍擊中目標的概率為：

因此3個人分別向目標發射1槍3彈都脫靶的概率為：

剖析上述錯誤在于將相互獨立事件同時發生的事件當成互斥事件來考慮，認為“3彈都未中”的對立事件是“3彈都中”.而事實上，這兩者不是對立事件.正確的解法應為：

甲、乙、丙脫靶的概率分別為

因此3彈都脫靶的概率是

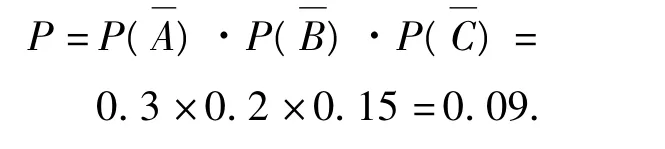
例6 甲投籃命中率為0.8，乙投籃命中率為0.7，每人投3次，2人恰好都命中2次的概率是多少?

錯解設“甲恰好投中2次”為事件A，“乙恰好投中2次”為事件B，則2人都恰好投中2次為事件A+B，于是

剖析本題錯誤的原因是把相互獨立并同時發生的事件當成互斥事件來考慮，將2人都恰好投中2次理解為“甲恰好投中2次”與“乙恰好投中2次”的和.互斥事件是指2個事件不可能同時發生;2個事件相互獨立是指一個事件的發生與否對另一個事件發生與否沒有影響.它們雖然都描繪了2個事件間的關系，但所描繪的關系根本不同.正確解法如下：

設“甲恰好投中2次”為事件A，“乙恰好投中2次”為事件B，且A，B相互獨立，則2人都恰好投中2次為事件A·B，于是

類型4 “互斥事件”與“對立事件”概念混同

例7 甲、乙2名同學分別解1道數學題，每個人解出這道題的概率都是0.6，求至少有1個人解出這道題的概率.

錯解甲、乙2人都解不出題的概率都是1-0.6=0.4，從而2位同學都解不出的概率是0.4+0.4=0.8，因此至少有1個人解出的概率為1-0.8=0.2.

剖析上述錯解的原因是把“互斥事件”與“對立事件”混同，互斥事件與對立事件的聯系與區別主要體現在以下3個方面：

(1)2個事件對立，則必定互斥，但互斥并不一定對立;

(2)互斥的概念適用于多個事件，但對立的概念只適用于2個事件;

(3)2個事件互斥只表明這2個事件不能同時發生，即至多有1個發生，但也可以2個都不發生，而對立事件則表示它們有且只有1個發生.

因此，上述問題的正確解法應為：

甲、乙2名同學解出這道題的概率分別為

甲、乙2名同學解不出這道題的概率分別為

因此甲、乙都解不出這道題的概率為

至少有1個人解出_這道題的概率是

例8 已知8支球隊中有3支弱隊，以抽簽方式將這8支球隊分為A，B兩組，每組4支.求：

(1)A，B兩組中有1組恰有2支弱隊的概率;

(2)A組中至少有2支弱隊的概率.

(2)A組中至少有2支弱隊包含2種情形，即A組中有2支弱隊而B組中有1支弱隊，或者A組中有3支弱隊而B組中沒有弱隊.由互斥事件概率的定義，得A組中至少有2支弱隊的概率是

剖析在錯解(1)中利用的是等可能事件概率的計算，但在計算過程中忽視了“A，B兩組中有1組恰有2支弱隊”有2種情形，即A組有2支弱隊或B組有2支弱隊的情形.在(2)中混淆了互斥事件與對立事件的概念，A組中有2支弱隊與B組中有1支弱隊不是對立事件，而是同一件事件，因此出現了錯誤.正確解法如下：

本題著重介紹了較為復雜的等可能事件的概率計算方法和計算過程中容易出現的錯誤.這類問題一般有3種解法：(1)直接運用公式和已學過的排列組合知識求出;(2)將復雜的事件分成幾個互斥事件，然后利用概率加法公式來解決;(3)類似于排列組合的間接法，先求出對立事件的概率，再求所求事件的概率，“至多至少”問題或多元復雜問題用這種方法較簡捷.這3種方法都是常用方法，必須熟練掌握.