和圖形變換有關的探究題

●勞海峰 (平水鎮中學 浙江紹興 312050)

綜觀近幾年的中考試題，筆者發現出現了一些培養學生探索精神、創新能力的探究題.其中操作型探究題主要以幾何圖形為背景，經軸對稱、平移、旋轉、相似變換構造新圖形，從形狀和位置變化中去探求全等、相似、函數、方程等知識間的內在聯系.通過觀察圖形在變化過程中所隱含的規律，猜想結論、證明等，是解決此類問題的基本策略.下面通過具體分析，說明此類問題的解題策略.

1 軸對稱有關的操作型探究題

解決這類問題的方法是先一般再特殊，即先找到一般性的規律然后退至特殊情形找到定值.

例1 閱讀下列材料：

小貝遇到一個有趣的問題：在矩形ABCD中，AD=8 cm，AB=6 cm.現有一動點P按下列方式在矩形內運動：它從點A出發，沿著與邊AB成45°的方向作直線運動，每次碰到矩形的一邊，就會改變運動方向，沿著與這條邊成45°的方向作直線運動，并且它一直按照這種方式不停地運動，即當點P碰到邊BC，沿著與邊BC成45°的方向作直線運動，當點P碰到邊CD，再沿著與邊CD成45°的方向作直線運動，……，如圖1所示.問點P第1次與點D重合前與邊相碰幾次，點P第1次與點D重合時所經過的路線的總長是多少?小貝的思考是這樣開始的：如圖2，將矩形ABCD沿直線CD折疊，得到矩形 A1B1CD.由軸對稱的知識，可得P2P3=P2E，P1A=P1E.

請你參考小貝的思路解決下列問題：

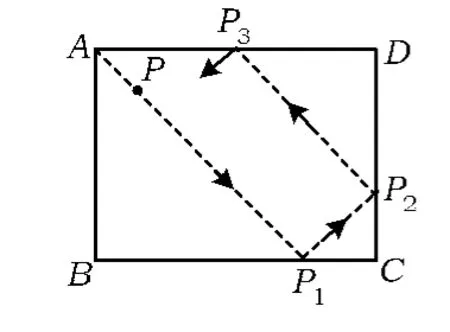
圖1

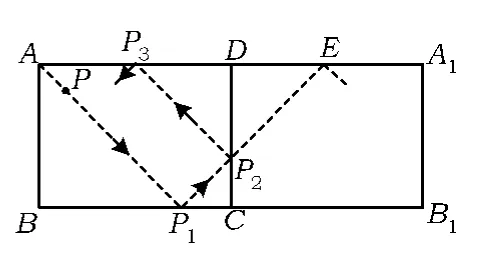
圖2

(1)點P第1次與點D 重合前與邊相碰_______次;點P從點A出發到第1次與點D重合時所經過的路徑的總長是_______cm.

(2)近一步探究：改變矩形ABCD中AD，AB的長，且滿足AD＞AB，動點P從點A出發，按照閱讀材料中動點的運動方式，并滿足前后連續2次與邊相碰的位置在矩形ABCD相鄰的2條邊上.若點P第1次與點B重合前與邊相碰7次，則AB ∶AD的值為_______.

圖3

點評本題是一道操作性探究題，主要根據軸對稱知識進行探究.第(1)小題的解法可根據閱讀材料中小貝的思考：“將矩形ABCD沿直線CD折疊，得到矩形 A1B1CD，由軸對稱的知識，可知P2P3=P2E，P1A=P1E”.思路延續得出矩形A2B2C1D1、矩形 A3B3C2D2……，然后畫出路徑.總路程是線段P1A=P1E=…=6的n倍.第(2)小題與第(1)小題有著密切的關系，矩形全等可得長和寬都相等.由解題思路示意圖，可知AB長的5倍等于CD長的4倍，即AB ∶AD的值為4∶5.

2 與平移有關的操作型探究題

解決這類問題的方法是由特殊值到一般規律，以靜制動.將平移后所得點的坐標根據橫、縱坐標的幾何意義把它表示出來，得到一個用變量表示的定值，以不變應萬變.

圖4

圖5

例2 探究 (1)如圖4，已知線段AB，CD，其中點分別為E，F.

①若 A(-1，0)，B(3，0)，則點 E 的坐標為_______;

②若 C(-2，2)，D(-2，-1)，則點 F 的坐標為_______.

(2)如圖5，已知線段AB的端點坐標為A(a，b)，B(c，d)，求出圖中 AB中點 D的坐標(用含 a，b，c，d的代數式表示)，并給出求解過程.

歸納 無論線段AB處于直角坐標系中的哪個位置，當其端點坐標為 A(a，b)，B(c，d)，AB 中點為 D(x，y)時，x= ______，y = ______(不必證明).

①求出交點A，B的坐標;

②若以A，O，B，P為頂點的四邊形是平行四邊形，請利用上面的結論求出頂點P的坐標.

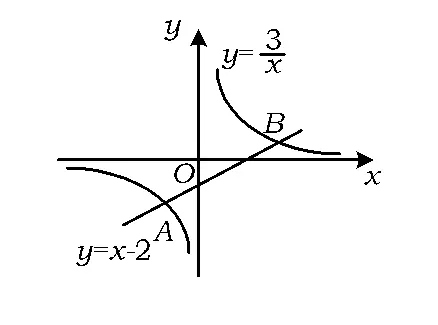
圖6

圖7

(2)如圖7，過點A，D，B分別作 x軸的垂線，垂足分別為 A'，D'，B'，則

因為D為AB的中點，由平行線分線段成比例定理得

運用 ①由題意得

圖8

解得 x=3，y=1 或 x=-1，y=-3，

即交點的坐標為 A(-1，-3)，B(3，1).

②如圖8，當AB為對角線時，由上面的結論知AB中點M的坐標為(1，-1).由平行四邊形對角線互相平分，知OM=OP，即M為OP的中點，從而點P坐標為(2，-2).同理可得分別以OA或OB為邊時，點 P 的坐標分別為(4，4)，(-4，-4).因此滿足條件的點P有3個，坐標分別是(2，-2)，(4，4)，(-4，-4).

3 與旋轉有關的操作型探究題

解決與旋轉有關的操作型探究題，需認真觀察圖形不放過一個細節，看清旋轉的角度和方向，找準旋轉前后的相關角與邊.在旋轉的過程中，弄清變與不變的量;在解決這類問題時，通常將其轉換成全等形求解.根據旋轉變換的特征，找到對應的全等形，通過線段、角的轉換達到求解的目的.

圖9

圖10

圖11

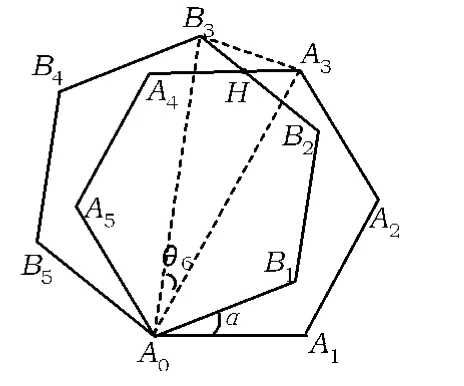
圖12

例3 課題 2個重疊的正多邊形，其中的一個繞某一個頂點旋轉所形成的有關問題.

實驗與論證 設旋轉角∠A1A0B1=α(α＜∠A1AOA2)，θ3，θ4，θ5，θ6所表示的角如圖9 ～12 所示.

(1)用含 α的式子表示角的度數：θ3=________，θ4= ______，θ5= ______.

(2)如圖9～12，連結A0H，在不添加其他輔助線的情況下，是否存在與直線A0H垂直且被它平分的線段?若存在，請選擇其中一個圖給出證明;若不存在，請說明理由.

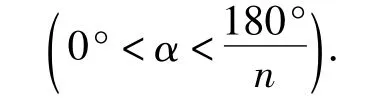
(3)設 θn與上述“θ3，θ4，…”的意義一樣，請直接寫出θn的度數.

(4)試猜想在正n邊形的情況下，是否存在與直線A0H垂直且被它平分的線段?若存在，請將這條線段用相應的頂點字母表示出來(不要求證明);若不存在，請說明理由.

解(1)60°-α，α，36°-α.

(2)存在.下面選圖9進行證明.

如圖13，直線A0H垂直平分A2B1.證明如下：

證明由△A0A1A2≌△A0B1B2，得

又由∠A0A2H=∠A0B1H=60°，得

于是點 H在線段 A2B1的垂直平分線上.又由A0A2=A0B1，得點A0在線段 A2B1的垂直平分線上，從而直線A0H垂直平分A2B1.

點評在第(1)，(2)小題中，筆者利用了旋轉后形狀不變、對應角線段相等求解;第(3)，(4)小題與前2個小題有密切關系，用到了正多邊形的外接圓知識、“在同圓或等圓中，如果2個圓心角、2條弧、2條弦、2個弦心距中有1個量相等，那么它們所對應的其余各個量都相等”和分類討論思想.本題利用旋轉的圖形不變性，探索圖形在旋轉過程中的有關規律，讓學生體驗圖形旋轉變換的性質，同時也考查了空間想象、規律探索、推理能力以及分析問題、解決問題的能力.

圖13

4 與相似有關的操作型探究題

解決與相似有關的探究題，關鍵要抓住哪些是平行線段、哪些是相似三角形、哪些線段可以得出相似比等.

例4 問題背景(1)如圖 14，在△ABC中，DE∥BC分別交AB，AC于點 D，E，過點 E作EF∥AB交 BC于點 F.請按圖示數據填空：

圖14

四邊形DBFE的面積S= _______，△EFC的面積 S1=________，△ADE 的面積為_______.

探究發現 (2)在第(1)小題中，若 BF=a，FC=b，DE 與 BC 的距離為 h，證明：S2=4S1S2.

拓展遷移 (3)如圖15，?DEFG的4個頂點在△ABC的3條邊上，若△ADG，△DBE，△GFC的面積分別為2，5，3，試利用第(2)小題中的結論求△ABC的面積.

(1)解 S=6，S1=9，S2=1.

(2)證明 由 DE∥BC，EF∥AB，知四邊形DBFE為平行四邊形，因此

圖15

圖16

(3)解 如圖16，過點G作GH∥AB交BC于點H，則四邊形DBHG為平行四邊形，從而由四邊形DEFG為平行四邊形，得

點評第(1)，(2)小題主要考查了相似三角形的面積之比等于相似比的平方;利用相似證明，可先找2對內角對應相等(對平行線型找平行線)，得△ADE∽△EFC;或先找一對內角對應相等，且看夾角是否對應成比例;若無對應角相等，則只需考慮3組對邊是否成比例.第(3)小題是利用了“探究 S2=4S1S2”、S△ABC=S△ADG+S△DBE+S?DEFG+S△GFC=S△ADG+S?DBHG+S△GHC求解.

綜上所述，探究性的數學問題具有不定向的解題思路，往往遵循從“合情推理”到“邏輯推理”的過程.而規律探究型在一定的條件狀態下，需探索發現有關數學對象所具有的規律性或不變性.