再談調和四邊形的性質及應用

●沈文選 (湖南師范大學數學奧林匹克研究所 湖南長沙 410081)

筆者在文獻［1］中介紹了調和四邊形的7條性質及7道應用的例題.在此，再介紹調和四邊形的一些有趣性質及應用的例子.

性質8 圓內接四邊形為調和四邊形的充要條件是該四邊形4個頂點與不在其圓上一點的連線交圓于4點為一正方形4個頂點.

圖1

證明如圖1，四邊形ABCD內接于⊙O，點P不在⊙O的圓周上，直線 PA，PB，PC，PD分別交⊙O 于點 A'，B'，C'，D'.由割線或相交弦定理得

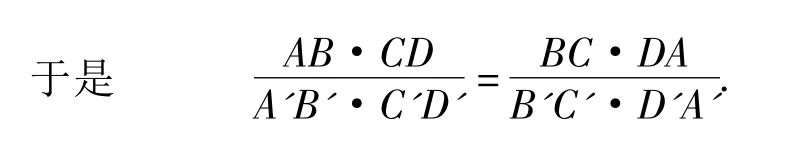
充分性 當A'，B'，C'，D'為正方形的4個頂點時，顯然AB·CD=BC·DA.

必要性 當AB·CD=BC·DA時，由PA·PA'=PB·PB'=PC·PC'=PD·PD'=k，可視點 A，B，C，D 的反演點為 A'，B'，C'，D'.由反演變換的性質，可知 A'，B'，C'，D'在 AB·CD=BC·DA的條件下為一正方形的4個頂點.

注由性質8給出了作調和四邊形的又一種方法.在文獻［2］中，也有如下定義：如果一個四邊形的頂點是一個正方形頂點的反形，那么被稱為調和四邊形.

性質9 圓內接四邊形為調和四邊形的充要條件是其一頂點對其余三頂點為頂點的三角形的西姆松線段被截成相等的兩段.

證明如圖2，設ABCD為圓內接四邊形，不失一般性.設點D在△ABC的3條邊BC，CA，AB上的射影分別為L，K，T，則LKT為點D的西姆松線段.此時 L，D，K，C 及 D，A，T，K 分別四點共圓，且CD，AD分別為其直徑.設此圓的半徑為R，由正弦定理得

從而四邊形ABCD為調和四邊形.

圖3

圖2

性質10 圓內接四邊形為調和四邊形的充要條件是一條對角線2個端點處的切線交點(或無窮遠點)與兩對角線的交點調和分割另一條對角線.

證明當圓內接四邊形為箏形時，易證得結論，這留給讀者自行證明.下證非箏形時的情形.

如圖3，設圓內接四邊形ABCD的2條對角線相交于點Q，在A，C處的2條切線相交于點P.由△QCD∽△QBA，△QAD∽△QBC，得

充分性 如圖3，當P，Q調和分割DB時，

此時點P，D，Q，B共線.由△PDC∽△PCB得

又由式(1)，(2)，(3)得

于是四邊形ABCD為調和四邊形.

必要性 如圖3，當ABCD為調和四邊形時，由性質1，知點 P，D，Q，B 共線，且有式(3)成立.由AD·BC=AB·CD，得

再注意到式(1)與式(3)，得

于是點P，Q調和分割DB.

性質11 圓內接四邊形為調和四邊形的充要條件是2條鄰邊之比等于此2條鄰邊所夾對角線分另一條對角線為2段對應之比開平方.

證明如圖4，設圓內接四邊形ABCD的2條對角線AC與BD交于點Q.

當圓內接四邊形為箏形時，易證得結論，這也留給讀者自行證明.下證非箏形時的情形.

圖4

從而ABCD為調和四邊形.

必要性 當ABCD為調和四邊形時，由性質1，知點A，C處的切線與直線DB共點于P，如圖4.于是，注意到面積關系與正弦定理，得

注由性質4知，在調和四邊形中，對角線的中點是其等角共軛點.如圖4，設M為AC的中點，

性質12 在調和四邊形ABCD中，點P在對角線 BD上，記 O，O1，O2分別為四邊形 ABCD，△BCP，△ABP的外接圓圓心，則直線BO平分線段O1O2.

證法1 如圖5，聯結BO1，BO2，OO1，OO2.設 M 為AC的中點，則由調和四邊形的 性 質 4，知 ∠ABP =∠CBM，即∠ABM=∠CBP.

設直線BO交O1O2于點Q，此時

圖5

注意到當一個角的2條邊與另一角的2條邊對應垂直時，這2個角相等或相補，得

于是，由正弦定理得

證法2 如圖5，設M為AC的中點.由性質4，知∠CBM=∠ABP，即∠CBD=∠ABM.又由∠BDC=∠BAM，得△DBC∽△ABM，從而

作△BCP，△ABP的外接圓，過點B作⊙O的切線分別交⊙O1，⊙O2于點 E，F，連結 CE.則由

而MA=CM，于是 BE=BF.作 O1E'⊥EB 于點 E'，作 O2F'⊥BF 于點 F'.由垂徑定理，知 E'，F'分別為EB，BF的中點.在直角梯形O1E'F'O2中，BO即為其中位線所在的直線，故它一定平分線段O1O2.

下面給出一些應用的例子.

例1 設ABCD是一個圓內接四邊形，點P，Q和R分別是D到直線BC，CA和AB的射影，證明：PQ=QR的充要條件是∠ABC和∠ADC角平分線的交點在線段AC上.

(2003年第44屆IMO試題)

證明如圖6，由性質9，知PQ=QR的充要條件是ABCD為調和四邊形.又由調和四邊形的性質3，知∠ABC和∠ADC的角平分線的交點在線段AC上的充要條件是ABCD為調和四邊形.故PQ=QR的充要條件是∠ABC和∠ADC的角平分的交點在線段AC上.

例2 已知直線上的3個定點依次為A，B，C，Γ為過點A，C且圓心不在AC上的圓，分別過點A，C且與圓Γ相切的直線交于點P，PB與圓Γ交于點Q.證明：∠AQC的平分線與AC的交點不依賴于圓Γ的選取. (2004年第45屆IMO預選題)

圖6

圖7

圖8

證明如圖7，點Q可在劣弧上，也可在優弧上.不失一般性，設點Q在劣弧上，直線PB與圓Γ的另一交點為Q'.由調和四邊形的性質1，知AQ'CQ為調和四邊形.設∠AQC的平分線交AC于點T，則由角平分線的性質，知.又由性質11，在調和四邊形AQ'CQ中，有

故點T不依賴于圓Γ的選取.

例3 在銳角△ABC中，AB＞AC，M是邊BC的中點，P是△ABC內的一點，使得∠MAB=∠PAC.設△ABC，△ABP，△ACP的外心分別為O，O1，O2，證明：直線 AO 平分線段 O1O2.

(2010年國家集訓隊選拔賽試題)

故圓內接四邊形ABDC為調和四邊形.于是由性質12知直線AO平分線段O1O2.

注由性質12，知例3的條件“P是△ABC內一點”，可改為“P是△ABC的外接圓內一點”，即圖8中的線段AD上的點(異于端點)均可.

例4 設銳角△ABC的外接圓為W，過點B，C作W的2條切線，相交于點P.連結AP交BC于點D，點 E，F 分別在邊 AC，AB 上，使得 DE∥BA，DF∥CA.

(1)求證：F，B，C，E 四點共圓;

(2)若記過點 F，B，C，E 的圓的圓心為 A1，類似地定義 B1，C1，則直線 AA1，BB1，CC1共點.

(2005年國家集訓隊測試題)

證明(1)如圖9，欲證 F，B，C，E四點共圓，只需證

因此欲證式(7)，只需證

設AP交圓W于點Q，連結BQ，QC.由調和四邊形性質4，知ABQC為調和四邊形.由性質11，知在調和四邊形ABQC中，式(8)顯然成立，故 F，B，C，E四點共圓.

圖9

圖10

由△AM1N1與△ABC位似，得

從而由第(1)小題知，F1，M1，N1，E1四點共圓.同理可得，F1，M1，S1，T1及 S1，T1，N1，E1分別四點共圓.于是

即 M1，S1，T1，N1，E1五點共圓.由對稱性，知點 F1也在此圓上，即六點共圓.

設此六點圓的圓心為O.由于⊙OA1與⊙O的位似中心為A，因此直線AA1過點O.同理可得，直線BB1，CC1也過點O.

［1］ 沈文選.論調和四邊形的性質及應用——兼談全國高中數學聯賽2道加試題的解法［J］.中學教研(數學)，2010(10)：35-39.

［2］ 沈文選.幾何瑰寶——平面幾何500名題暨1 000條定理［M］.哈爾濱：哈爾濱工業大學出版社，2010.