新課程高考創(chuàng)新題型剖析

●黃根聯(lián) (職業(yè)技術(shù)學(xué)校 浙江浦江 322200)

近幾年全國各地高考試題逐漸強(qiáng)調(diào)創(chuàng)新意識和應(yīng)用意識的考查，強(qiáng)調(diào)理論與實(shí)踐相統(tǒng)一.一些新穎的試題背景、類型在近幾年的試卷中從無到有，從粗糙到精致，這些變化都體現(xiàn)了高考命題在有意識地將新課程的理念落實(shí)到高考試題中.最近幾年的新課程高考變革，在穩(wěn)定中求發(fā)展，在漸變中求提升.既重視了基礎(chǔ)知識、基本思想方法的考查;又重視了數(shù)學(xué)本質(zhì)、數(shù)學(xué)文化、數(shù)學(xué)精神的體現(xiàn).命題專家精心設(shè)計(jì)了一批有特色、有味道、有思想的新穎、別致的能力型考題.

1 結(jié)論開放，培養(yǎng)學(xué)生的探究精神

“開放”是相對于“封閉”而言的，傳統(tǒng)數(shù)學(xué)題多屬封閉型.譬如一種明確的條件，一種確定的結(jié)論，甚至連解答過程和方法都是確定的.開放題與此相異.有的有明確的條件而無明確的結(jié)論，甚至連結(jié)果存在與否也不知道;有的有明確結(jié)論而無明確的條件，甚至連條件是否存在還不知道.研究性學(xué)習(xí)逐步在數(shù)學(xué)學(xué)科中滲透，它的精髓是開放式教學(xué)，在高考中的體現(xiàn)就是開放性試題，體現(xiàn)了數(shù)學(xué)活動的開放性和非常規(guī)化，以及活動過程中的探究性、實(shí)踐性和創(chuàng)新性，是高考數(shù)學(xué)原創(chuàng)題命制的方向之一.一般考試題目的開放度是比較小的，這有利于評價(jià)的度的把握.開放可以分為條件開放、結(jié)論開放、解答方式多樣等.

例1 已知函數(shù)f(x)=|x2-ax-b|(x∈R，b≠0)，給出以下3個條件：

(1)存在x0∈R，使得f(-x0)≠f(x0);

(2)f(3)=f(0)成立;

(3)f(x)在區(qū)間［-a，+∞)上是增函數(shù).

若f(x)同時滿足條件_______和_______(填入2個條件的編號)，則f(x)的一個可能的解析式為f(x)= ______.

分析當(dāng)滿足條件(1)和(2)時，y=|x2-3x+1|等;當(dāng)滿足條件(1)和(3)時，y=|x2+2x+1|等;滿足條件(2)和(3)時，y=|x2+3x-9|等.

例2 如圖1是某汽車維修公司的維修點(diǎn)環(huán)形分布圖，公司在年初分配給A，B，C，D這4個維修點(diǎn)某種配件各50件，在使用前發(fā)現(xiàn)需將A，B，C，D這4個維修點(diǎn)的這批配件分別調(diào)整為40，45，54，61件，但調(diào)整只能在相鄰維修點(diǎn)之間進(jìn)行，那么要完成上述調(diào)整，最少的調(diào)動件次(n件配件從一個維修點(diǎn)調(diào)整到相鄰維修點(diǎn)的調(diào)動件次為n)為( )

A.18 B.17 C.16 D.15

圖1

圖2

分析由圖2，可得f=10+1+5=16.應(yīng)選C.

探究將上述選擇題改為探究題：

(1)請?jiān)O(shè)計(jì)一個調(diào)動件次最少的方案，并說明理由;

(2)請找出調(diào)動件次最少的所有方案并說明理由.

點(diǎn)評本題的背景是運(yùn)籌學(xué)問題，可以給出如下方程組解法：

設(shè)A→B件數(shù)為x1(當(dāng)x1＜0時，為B→A，以下同)，B→C為x2件，C→D為x3件，D→A為x4件，則

這里，4個未知數(shù)滿足3個獨(dú)立方程，因此無法解出這4個未知數(shù).由基本量思想，可用x1表示x2，x3與 x4，解得

故調(diào)動總件數(shù)為

其最小值為16.

2 定義新知，重視學(xué)生的創(chuàng)新意識

重視創(chuàng)新意識和實(shí)踐能力的培養(yǎng)，這是增加到新大綱中的一項(xiàng)重要目的和基本原則.新大綱對創(chuàng)新意識和實(shí)踐能力的含義作了必要的闡釋，并提供了“實(shí)習(xí)作業(yè)”、“研究性課題”等教育手段和一些具體的教學(xué)方法.在此類題目中，將創(chuàng)新元素具體地落實(shí)到新定義、新運(yùn)算中，與新課標(biāo)理念完全吻合，也是高考命題的熱點(diǎn)和必然趨勢.

例3 在R上定義運(yùn)算⊙：a⊙b=ab+2a+b，則滿足x⊙(x-2)＜0的實(shí)數(shù)x的取值范圍為( )

點(diǎn)評本題為定義新運(yùn)算型試題，正確理解新定義是解題的關(guān)鍵.只要譯出條件，就能轉(zhuǎn)化為一元二次不等式求解.

3 素材改編，探求教材內(nèi)容新意

以某些傳統(tǒng)內(nèi)容為載體進(jìn)行適當(dāng)改編，并賦予新意，設(shè)計(jì)出一些新穎的題目是近幾年高考的一大亮點(diǎn).此類試題形式新穎、解法多樣.而新情境的創(chuàng)設(shè)是原創(chuàng)的，對所有學(xué)生都是公平的，同時還能較好地考查學(xué)生的綜合能力，備受命題者的青睞.

例4 如圖3，一個正五角星薄片(其對稱軸與水面垂直)勻速地升出水面，記t時刻五角星露出水面部分的圖形面積為S(t)(S(0)=0)，則導(dǎo)函數(shù)y=S'(t)的圖像大致為( )

圖3

分析本題考查函數(shù)圖像、導(dǎo)數(shù)圖像、導(dǎo)數(shù)的實(shí)際意義等知識，重點(diǎn)考查的是學(xué)生對數(shù)學(xué)的探究能力.此題的命題角度新穎、獨(dú)特、創(chuàng)新，可以使用排除法求解，答案為A.

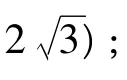
(1)求A，ω的值和點(diǎn)M，P間的距離;

(2)應(yīng)如何設(shè)計(jì)，才能使折線段賽道MNP最長?

分析(1)依題意得

(2)在 △MNP 中，∠MNP=120°，MP=5.設(shè)∠PMN=θ，則0°＜θ＜60°.由正弦定理得

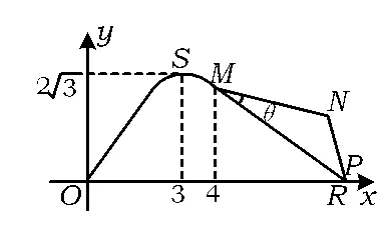
圖4

又因?yàn)?°＜θ＜60°，所以當(dāng) θ=30°時，折線段賽道MNP最長，即將∠PMN設(shè)計(jì)為30°時，折線段道MNP最長.

點(diǎn)評三角函數(shù)與實(shí)際應(yīng)用性問題是近幾年新課程高考命題的一個熱點(diǎn).

4 立意深刻，挖掘?qū)W生的學(xué)習(xí)潛能

近幾年來，高等數(shù)學(xué)的基本思想、基本方法和基本問題為高考試題的命制提供了新的背景和新的思路.

例6 如圖5，在平面直角坐標(biāo)系中，Ω是一個與x軸的正半軸、y軸的正半軸分別相切于點(diǎn)C，D的定圓所圍成的區(qū)域(含邊界)，A，B，C，D 是該圓的四等分點(diǎn).若點(diǎn) P(x，y)，點(diǎn) P'(x'，y')滿足 x≤x'且y≥y'，則稱點(diǎn)P優(yōu)于點(diǎn)P'.如果Ω中的點(diǎn)Q滿足：不存在Ω中的其他點(diǎn)優(yōu)于點(diǎn)Q，那么所有這樣的點(diǎn)Q組成的集合是劣弧 ( )

分析由題意知，若點(diǎn)P優(yōu)于點(diǎn)P'，則點(diǎn)P在點(diǎn)P'的左上方.因?yàn)楫?dāng)點(diǎn)Q在)DA上時，左上的點(diǎn)不在圓上，不存在其他優(yōu)于點(diǎn)Q的點(diǎn)，所以點(diǎn)Q組成的集合是劣弧.應(yīng)選D.

點(diǎn)評本題是新定義圖形的一種解析幾何模型的新穎題，實(shí)質(zhì)是借助定義，確定點(diǎn)Q形成的圖形，然后恰當(dāng)?shù)剡x擇.

圖5

5 信息交匯，培養(yǎng)學(xué)生的轉(zhuǎn)換能力

信息試題是高考數(shù)學(xué)試題的創(chuàng)新源，信息題就是根據(jù)文字、圖表、圖形等給出的數(shù)據(jù)信息，通過整理、加工、處理等手段去解決實(shí)際問題的一類題目.在解答信息題時，首先要仔細(xì)閱讀題目所提供的材料，從中捕捉有關(guān)信息(譬如數(shù)據(jù)間的關(guān)系與規(guī)律圖像的形狀特點(diǎn)、變化趨勢等)，然后對這些信息進(jìn)行加工處理，并聯(lián)系相關(guān)數(shù)學(xué)知識，從而實(shí)現(xiàn)信息的轉(zhuǎn)換，使問題順利獲解.

例7 記實(shí)數(shù) X1，X2，…，Xn中的最大數(shù)為max{X1，X2，…，Xn}，最小數(shù)為mix{X1，X2，…，Xn}.已知△ABC的3條邊長為 a，b，c(a≤b≤c)，定義它的傾斜度為

則“l(fā)=1”是“△ABC為等邊三角形”的 ( )

A.充分而不必要的條件

C.必要而不充分的條件

B.充要條件

D.既不充分也不必要的條件

分析若△ABC為等邊三角形，即a=b=c，則

因此l=1;若△ABC為等腰三角形，得

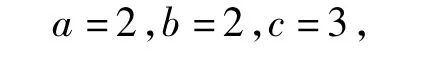
此時l=1仍成立.但△ABC不為等邊三角形，所以選項(xiàng)B正確.

點(diǎn)評集合和常用邏輯用語中的信息問題也不例外.這方面試題的破解一要認(rèn)真審題，二要結(jié)合集合、常用邏輯用語的意義.信息交匯問題因?yàn)樯婕暗降闹R背景新穎，因此對考生而言更具公平性，破解時更需獨(dú)立思考以分析、解決問題.

例8 若數(shù)列{an}滿足：對任意的n∈N*，只有有限個正整數(shù)m使得am＜n成立，記這樣的m的個數(shù)為(an)*，則得到一個新數(shù)列{(an)*}.例如，若數(shù)列{an}是1，2，3…，n，…，則數(shù)列{(an)*}是0，1，2，…，n-1，….已知對任意的 n∈N*，an=n2，則(a5)*= ______，((an)*)*= ______.

分析本題以數(shù)列為背景，通過創(chuàng)設(shè)適度開放，引導(dǎo)考生進(jìn)行適度的推理探索，此類題型可以說是新課標(biāo)高考數(shù)學(xué)試題的一大亮點(diǎn).答案為2，n2.

點(diǎn)評高考命題對數(shù)學(xué)思維能力作了新的闡釋，它不但包含了原大綱提到的三大數(shù)學(xué)能力，即邏輯思維能力、空間想象能力與計(jì)算能力，而且將其擴(kuò)展為直觀感知、觀察發(fā)現(xiàn)、歸納類比、空問想象、抽象概括、符號表示、運(yùn)算求解、數(shù)據(jù)處理、演繹證明、反思與構(gòu)建等思維能力.這些正顯示了對數(shù)學(xué)探究能力的更高要求，這一點(diǎn)不僅說明了我國對數(shù)學(xué)問題的研究在高考的促進(jìn)下有了一定的發(fā)展，也為今后的教學(xué)指明了新的方向.

構(gòu)圖對新聞攝影作品的質(zhì)量及實(shí)效性產(chǎn)生直接影響，良好的構(gòu)圖能夠快速吸引觀眾視線，提升攝影作品的震撼力與影響力。[5]與藝術(shù)攝影對構(gòu)圖的要求不同，新聞攝影構(gòu)圖應(yīng)以營造良好的現(xiàn)場感為主，使圖片具有較強(qiáng)的視覺沖擊力，需攝影人員良好地應(yīng)用攝影技巧及藝術(shù)手法，提升攝影作品靈活性，使其具有獨(dú)特的藝術(shù)感染力。

6 創(chuàng)設(shè)情境，體現(xiàn)學(xué)生能力差異

一些綜合型的情境創(chuàng)設(shè)能給學(xué)生一個很好的施展才華、發(fā)揮能力的機(jī)會.高考是為高校招生而進(jìn)行的選拔性考試，而此類以能力立意的創(chuàng)新試題非常適合設(shè)計(jì)一些既體現(xiàn)數(shù)學(xué)學(xué)科特點(diǎn)，又考查繼續(xù)學(xué)習(xí)潛能的試題.既能很好地體現(xiàn)新課標(biāo)的理念，又有利于實(shí)現(xiàn)數(shù)學(xué)高考的選拔功能，可謂一箭雙雕.

例9 甲、乙2人用4張撲克牌(分別是紅桃2，紅桃3，紅桃4，方片4)玩游戲，他們將撲克牌洗勻后，背面朝上放在桌面上，甲先抽，乙后抽，抽出的牌不放回，各抽1張.

(1)設(shè)(i，j)分別表示甲、乙抽到的牌的數(shù)字，寫出甲、乙2人抽到的牌的所有情況.

(2)若甲抽到紅桃3，則乙抽出的牌面數(shù)字比3大的概率是多少?

(3)甲、乙約定：若甲抽到的牌的牌面數(shù)字比乙大，則甲勝，否則乙勝.你認(rèn)為此游戲是否公平，說明你的理由.

分析(1)甲、乙2人抽到的牌的所有情況(方片 4 用4'表示)為：(2，3)、(2，4)(2，4')、(3，2)、(3，4)、(3，4')、(4，2)、(4，3)、(4，4')、(4'，2)、(4'，3)、(4'，4)，共有 12 種不同情況.

例10 若A，B是拋物線y2=4x上不同的2個點(diǎn)，弦AB(不平行于y軸)的垂直平分線與x軸相交于點(diǎn)P，則稱弦AB是點(diǎn)P的一條“相關(guān)弦”.已知當(dāng)x＞2時，點(diǎn)P(x，0)存在無窮多條“相關(guān)弦”.給定 x0＞2.

(1)求證：點(diǎn)P(x0，0)的所有“相關(guān)弦”的中點(diǎn)的橫坐標(biāo)相同.

(2)試問：點(diǎn)P(x0，0)的“相關(guān)弦”的弦長中是否存在最大值?若存在，求其最大值(用x0表示);若不存在，請說明理由.

分析此題是一道綜合創(chuàng)新題，結(jié)合了新定義、探索性等創(chuàng)新元素.

(1)設(shè) AB為點(diǎn) P(x0，0)的任意一條“相關(guān)弦”，且點(diǎn) A，B 的坐標(biāo)分別是(x1，y1)，(x2，y2)(x1≠x2)，則

因?yàn)閤1≠x2，所以 y1+y2≠0.設(shè)直線 AB的斜率為k，弦 AB 的中點(diǎn)是 M(xm，ym)，則

從而AB的垂直平分線l的方程為

又由點(diǎn) P(x0，0)在直線 l上，得

而 ym≠0，于是

故點(diǎn)P(x0，0)的所有“相關(guān)弦”的中點(diǎn)的橫坐標(biāo)都是x0-2.

(2)由第(1)小題知，弦AB所在直線的方程是

代入y2=4x中，整理得

則x1，x2是方程(1)的2個實(shí)根，且

設(shè)點(diǎn)P的“相關(guān)弦”AB的弦長為l，則

綜上所述，當(dāng) x0＞3時，點(diǎn) P(x0，0)的“相關(guān)弦”的弦長中存在最大值，且最大值為2(x0-1);當(dāng)2＜x0≤3時，點(diǎn) P(x0，0)的“相關(guān)弦”的弦長中不存在最大值.

高考試題對創(chuàng)新意識的考查，主要是要求考生不僅能理解一些概念、定義，掌握一些定理、公式，更重要的是能夠應(yīng)用這些知識和方法解決數(shù)學(xué)和現(xiàn)實(shí)生活中比較新穎的問題.數(shù)學(xué)教育的目的不只是讓學(xué)生掌握一些知識，也不是把每個學(xué)生都培養(yǎng)成數(shù)學(xué)家，而是把數(shù)學(xué)作為材料和工具，通過數(shù)學(xué)的學(xué)習(xí)和訓(xùn)練，在知識和方法的應(yīng)用中提高綜合能力和基本素質(zhì)，形成科學(xué)的世界觀和方法論.因此，高考試題加強(qiáng)對創(chuàng)新意識的考查，其意義已超出了數(shù)學(xué)學(xué)習(xí)，對提高學(xué)習(xí)和工作能力、對今后的人生都有重要的意義.