四開關三相永磁同步電機磁場定向控制系統

王曉丹， 李 端， 郭希錚

(1.河南理工大學電氣工程與自動化學院，河南焦作 454001;

2.北京交通大學電氣工程學院，北京 100044)

0 引言

20世紀70年代初，文獻［1］提出異步電機磁場定向的控制原理，該方法以其控制簡單、魯棒性好，以及快速的動態性能被廣泛研究。永磁同步電機(PermanentMagnetSynchronousMotor，PMSM)具有功率密度高、效率高、低速大轉矩及調速范圍寬等優點，在電動汽車、艦船驅動領域有著廣闊的應用前景［2］。磁場定向控制(Field Oriented Control，FOC)方法以其優良的性能也得到了廣泛應用。

傳統PMSM的FOC系統中，采用三相六開關逆變器(Six-Switch Three-Phase Inverter，SSTPI)供電。但是，由于電力電子器件是系統最為脆弱的一部分，因此當其出現故障時，如何采取相應的應對措施是學者研究的熱點［3］。通常的解決方法有兩種:第一種是采用開關器件冗余方法;第二種是實施四開關三相運行［4-6］。第一種方法會增加系統硬件成本，而第二種方法是低成本的選擇，且當其單獨應用于PMSM的FOC系統時，可以降低系統成本，并簡化系統拓撲結構。

四開關三相逆變器(Four Switch Three Phase Inverter，FSTPI)只有4個開關器件，與 SSTPI相比，只有4個開關矢量，并且沒有零矢量，其空間矢量脈寬調制方法(Space Vector Pulse Width Modulation，SVPWM)是應重點研究的問題［7］。本文以四開關三相PMSM的FOC系統為研究對象，首先分析了FSTPI空間矢量調制方法，其次分析了PMSM的FOC原理，并以此為基礎建立了系統的控制模型。分析結果表明:四開關三相PMSM的FOC系統可以穩定運行，并且具有較好的轉矩動態響應性能。

1 FSTPI空間矢量調制

四開關三相PMSM系統拓撲如圖1所示。與采用傳統SSTPI系統不同，FSTPI節省了1個橋臂，即節省了2只大功率全控開關器件，直流側增加了1只電容，但是電容耐壓值為SSTPI的1/2。

圖1 FSTPI-PMSM系統拓撲結構圖

1.1 電壓矢量表

定義Sa、Sb為開關變量，其中:Sa=1時表示A相上橋臂T1導通;Sa=0時表示A相下橋臂T3導通。因此，FSTPI共有22=4種開關狀態，每種開關狀態對應一定的三相電壓瞬時值。相對于SSTPI具有8個電壓矢量(6個有效電壓矢量，2個零矢量)，FSTPI開關矢量的分布還與負載連接方式有關，對于PMSM的FOC系統來說，相當于星型負載連接。FSTPI-PMSM電壓開關矢量表如表1所示，圖2是其空間分布。

表1 FSTPI電壓開關矢量表

圖2 FSTPI-PMSM系統開關矢量分布

上述開關矢量有如下特點:

(1)開關矢量幅值不同，|u2|=|u1|;

(2)不存在零矢量;

(3)只有4個開關矢量可以利用，控制自由度降低。

1.2 FSTPI空間矢量調制算法

設u*為合成的電壓矢量，根據脈沖等量原則:合成矢量與時間的乘積等于四個基本矢量與相應時間乘積之和，存在如下關系:

Ts為開關周期，t1、t2、t3、t4滿足式(2):

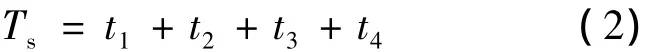
u*在靜止坐標系時表示為u*=uα*+juβ

*，

且FSTPI開關矢量存在以下關系:

可以得到式(3):

其中:t13=t1-t3，t24=t2-t4。

由式(3)可以得到:

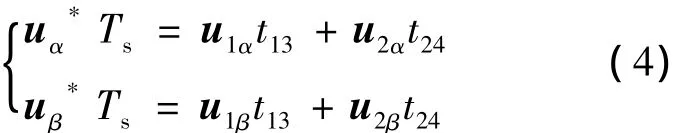
其中:u1α=-Ud/12，u1β=-Ud/4，u2α=Ud/4，u2β=-Ud/4。由式(4)可以得到:

由上文分析可知，結合式(2)、(5)無法求解t1、t2、t3、t4，且 FSTPI不存在零矢量，根據式(3)推得零矢量的作用時間為

由圖 2 可以看到，u1=-u3，u2=-u4，那么零矢量可以等效為以下3種方式:

(1)u1，u3同時作用，如圖3(a)所示;

(2)u2，u4同時作用，如圖3(b)所示;

(3)將零矢量分為kδT和(1-k)δT(0≤k≤1)兩部分，即u1，u3和 u2，u4共同作用，如圖3(c)所示;此時，計算得到的t1、t2、t3、t4如表2 所示。

由表2可以看出:當k=1時，即選擇矢量u1、u3共同作用等效為零矢量;當k=0時，即選擇矢量u2、u4共同作用等效為零矢量。由表2計算得到的t1、t2、t3、t4滿足式(2)、(5)。

圖3 FSTPI零矢量的選擇方式

表2 FSTPI不同扇區各矢量作用分布表

1.3 矢量切換順序

在SSTPI空間矢量算法中，通過插入零矢量，在不同扇區通過合理的選擇矢量開關順序，保證每次電路拓撲結構三個橋臂中只有一個橋臂的開關狀態發生變化，從而減少開關損耗。以第一扇區為例，選擇開關矢量u1(001)，u2(011)，那么其矢量切換順序為u0(000)—u1(001)—u2(011)—u7(111)—u2(011)—u1(001)—u0(000)。

這里所遵循的原則是每次切換時只有一個開關狀態發生變化。因此，在FSTPI中滿足此原則的矢量切換順序如圖4所示。

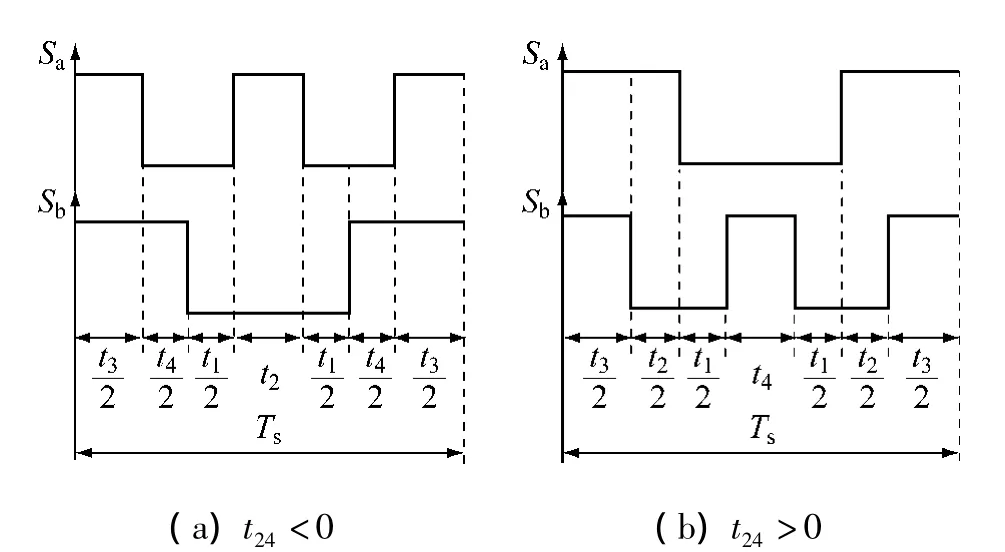
圖4 矢量切換順序

2 四開關三相PMSM的FOC系統實現

PMSM在同步旋轉坐標系下的dq軸數學模型［1］如下。

(1)電壓方程:

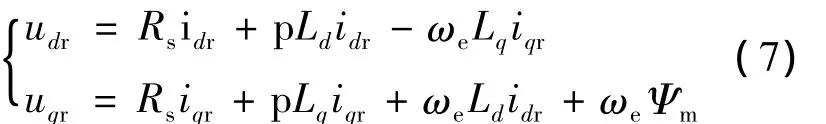
式中:p——微分算子;

Rs——定子電阻;

Ld、Lq——d、q軸等效電感;

P——電機極對數;

Ψm——轉子固有磁鏈。根據上述模型，四開關三相系統控制框圖如圖5所示。圖中:Is*為根據轉矩指令查表獲取的電流指定，通過MTPA曲線［9］得到d、q軸電流指令idr

*、iqr

*，電流指令與反饋相比較經過PI調節

對于FSTPI或SSTPI來說，其輸出電壓范圍是一定的。當PMSM轉速升高時，其轉子反電勢由永磁體產生而無法調節，電機定子電壓會超過逆變器最大輸出電壓uslim限制。圖5中將uslim與參考電壓幅值us比較后通過單向PI調節器產生弱磁電流分量Δidr，使得逆變器輸出最大線電壓并保持不變。

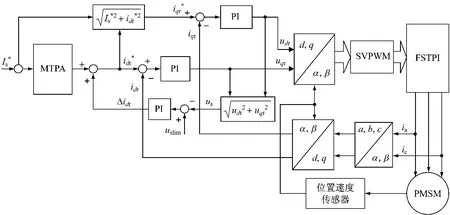
圖5 四開關三相PMSM的FOC系統控制框圖

3 仿真研究

為了研究FSTPI-PMSM的FOC系統性能，對圖5所示系統建模，并采用MATLAB進行仿真研究，其中SVPWM部分采用S_function建模。仿真參數設置如下。

(1)永磁電機:Rs=0.107 Ω，Ld=Lq=2.5 mH，Ψf=0.175，P=4;

(2)逆變器:C1=C2=3 300e-6 μF，Ud=330 V，fsw=10 kHz;

圖 6(a)，(b)，(c)比較了k=0，0.5，1 時，FSTPI-PMSM的FOC系統仿真結果，其中轉矩給定為20 N·m，電機轉速為320 r/min。圖6表明:選取不同的k值時，系統均能穩定運行;但是，k=0.5時的電流波形正弦性和轉矩脈動情況要明顯優于其他兩種情況;k=0時，轉矩脈動最大，電流波形中的諧波分量加大。圖6(d)為SSTPIPMSM系統仿真結果，相對于圖6(b)，其電流波形光滑，諧波分量減小，轉矩脈動降低。這表明，在減少系統成本和提高系統性能之間存在折中。

圖7為FSTPI-PMSM的FOC系統轉矩響應曲線，0.3 s時轉矩指令突增為30 N·m，0.35 s時轉矩突降為15 N·m，可以看到，電機輸出電磁轉矩能夠快速響應轉矩指令變化，保持了FOC系統轉矩動態響應快的特點。

在FSTPI中采用SVPWM算法時，其零矢量是將兩個位置互差180°的矢量同時作用來等效的。該方法所帶來的直接影響使得逆變器直流側的兩支電容電壓產生波動，如圖8所示，可以通過增加直流側電容值來增加電容儲能能量，從而減小電壓波動幅值。

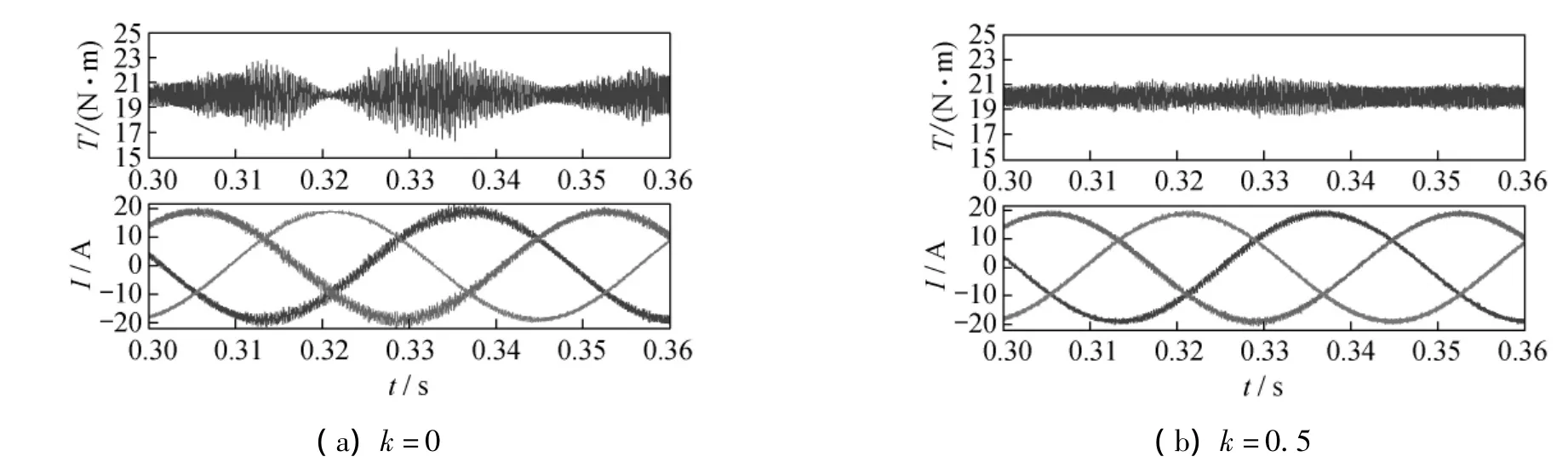
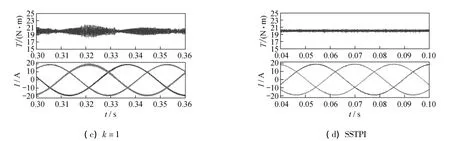
圖6 FSTPI-PMSM的FOC系統仿真結果

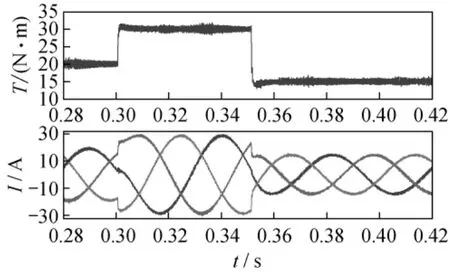
圖7 FSTPI-PMSM的FOC系統轉矩響應曲線

圖8 FSTPI直流側電容電壓波形

4 結語

本文將FSTPI應用于三相PMSM的FOC系統，針對其僅有4個有效電壓矢量，采用通過兩個互差180°的電壓矢量疊加等效的方法產生零矢量作用。通過對三種SVPWM策略進行仿真研究，結果表明:

(1)k=0.5時，即采用4個電壓矢量同時作用等效零矢量時，電機電流波形、轉矩脈動均得到了改善。

(2)FSTPI-PMSM的FOC系統保持了FOC系統轉矩動態響應快的特點，是一種具有實用前景的控制拓撲結構。

［1］Blaschke F.The principles of field orientation as applied to the new RANSVEKTOR closed-loop control system for rotating field machines［J］.Siemens Review，1972:217-220.

［2］金能強，何洪濤.稀土永磁電機的應用和發展狀況［J］.電工電能新技術，1995(3):17-21.

［3］Kastha D，Bose B K.Investigation of fault modes of voltage-fed inverter system for induction motor drive［J］.IEEE Transactions on Industry Applications，1994，30(4):1028-1038.

［4］Salazar L，Vasquez F C，Wiechmann E.On the characteristics of a PWM AC controller using four switches［J］.PESC’93，1993:307-313.

［5］Jacobina C B.Vector and scalar control of a four switch three phase inverter［J］.IAS，1990(5):2422-2429.

［6］Lee Hong Hee，Dzung P Q.The development of space vector PWM for four switch three phase inverter fed induction motor with DC-link voltage imbalance［J］.ICIT，2009:1-6.

［7］Beltrao De Rossiter Correa.A general PWM strategy for four-switch three-phase inverters［J］.IEEE Transactions on Power Electronics，2006，21(6):1618-1627.

［8］唐任遠.現代永磁電機理論與設計［M］.北京:機械工業出版社，1997.

［9］Hu Jun，Wu Bin.New integration algorithms for estimating motor flux over a wide speed range［J］.IEEE Transactions on Powe Electronics，2006，13(5):969-977.