無源控制的超混沌Chen系統的自適應同步

傅桂元，李鐘慎

（華僑大學機電及自動化學院，福建 泉州 362021）

無源控制的超混沌Chen系統的自適應同步

傅桂元，李鐘慎

（華僑大學機電及自動化學院，福建 泉州 362021）

在不同初始條件下，提出一種基于無源控制理論的控制方法，實現具有參數不確定性的兩超混沌Chen系統的自適應同步.通過引入自適應控制，在線估計系統的參數，并設計一個自適應無源控制器，使兩系統的同步誤差方程轉化為無源系統.根據無源系統理論，系統的動態誤差方程將穩定于狀態空間原點，即兩超混沌Chen系統完全同步.仿真結果表明，所設計的控制器簡單明了，控制方法有效.

超混沌Chen系統；同步；無源控制；自適應控制

近年來，人們提出各種控制方法實現兩混沌系統的同步，包括自適應控制［1］、反步法控制［2］、滑模變結構控制［3］、線性及非線性反饋控制［4］、主動控制方法［5］、線性矩陣不等式［6］等.但是，上述方法設計的控制器或過于復雜，或是只適用于具有參數嚴格反饋形式的一類混沌系統，在實際應用中仍受到很大的限制.對于存在振蕩的不穩定性系統，為了使系統內部穩定，可以依據無源理論構造反饋控制器，使得相應的閉環系統無源而保持內部穩定.文［7］將無源系統理論應用到非線性系統的鎮定.文［8］基于無源控制的方法，實現對Lorenz混沌系統的控制，使其穩定到零平衡點和非零平衡點.本文提出一種基于自適應無源控制的方法實現兩超混沌系統的同步.

1 無源控制系統

考慮仿射非線性系統，有

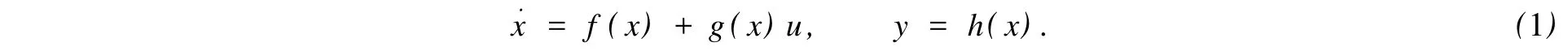
式（1）中：狀態變量x∈Rn；外部輸入u∈Rm；系統輸出y∈Rm；f和g的m列為光滑的向量場；h為光滑映射.

定義1 系統（1）稱為無源系統，如果其滿足對于?t≥0，存在一個實常數β，使得不等式

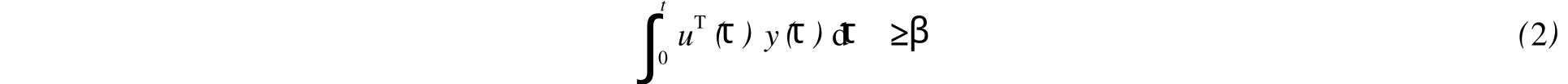
成立，或者存在ρ＞0和一個實常數β，使不等式

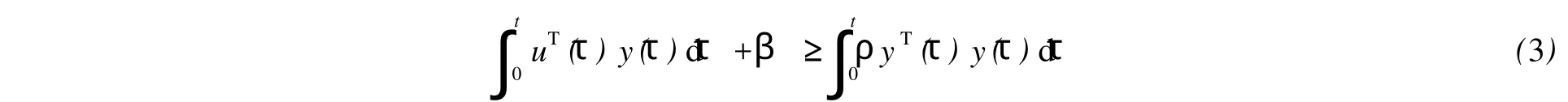
成立.

從定義1可以看出，無源非線性系統的物理意義非常明顯，即系統只能通過外部輸入來增加能量.從反方面考慮，可以利用無源系統的這個物理特性，通過施加外部控制來逐步減少非線性振蕩系統的能量，從而降低系統輸出幅度，實現系統的穩定.

引理1［9］如果系統為無源系統，令φ為光滑函數，則必然存在控制律u（t）=-φ（y），使非線性系統在平衡點處漸近穩定.

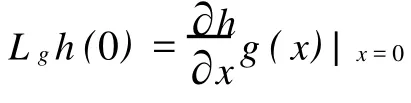
令z=θ（x），則系統（1）可以化為如下形式

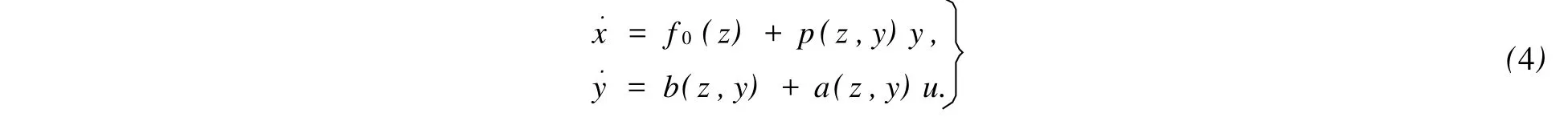
定理1 假定系統（1）為最小相位系統，x=0是系統（1）的平衡點.若系統（1）在x=0處具有相對階［1，1，…，1］，則系統（4）可以通過局部反饋控制等效為一個無源系統，且其選擇的反饋控制器為

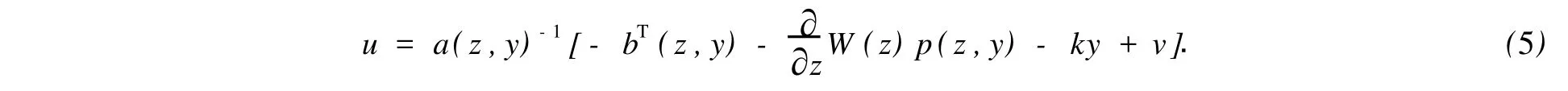
式（5）中：W（z）為f0（z）的Lyapunov函數；k為任意大于零的常數；v是與輸入u有關的外部輸入量.

證明 選取系統的Lyapunov函數為

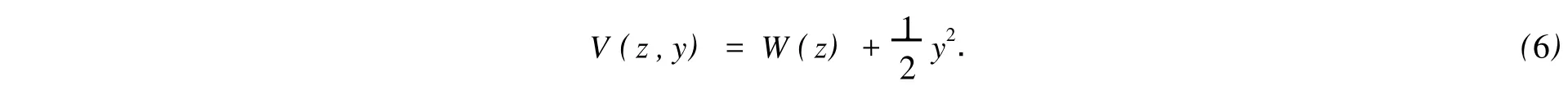
兩邊求導后，可得

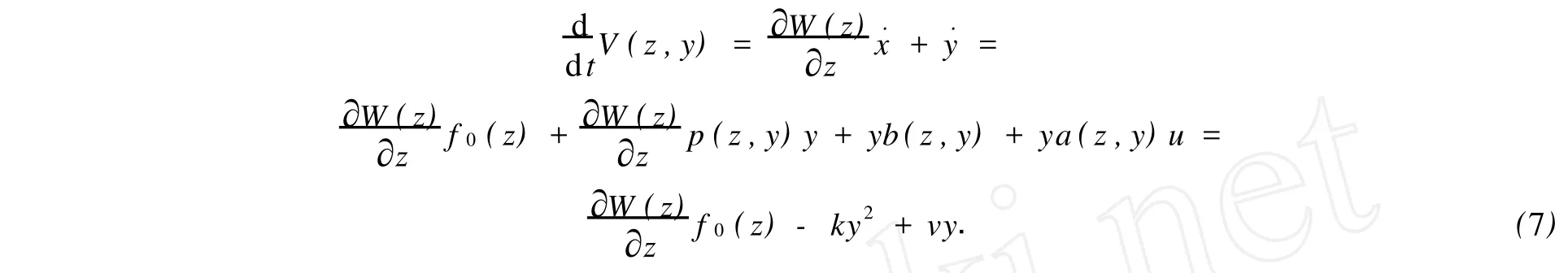
由于系統（1）為最小相位系統，即系統（4）也為最小相位系統，則有

由此可得

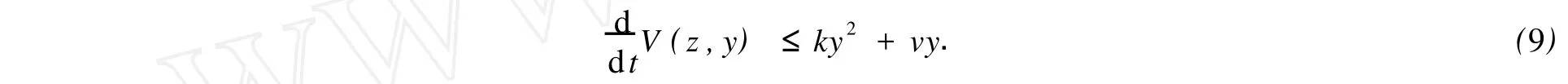
對式（9）兩邊積分可得

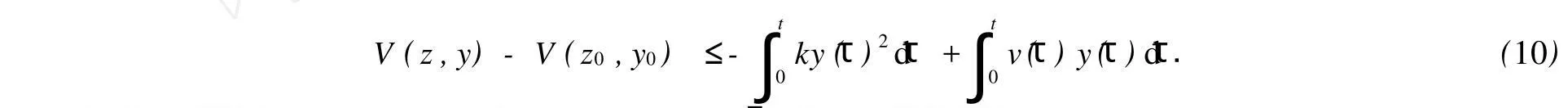
由式（6）可知，V（z，y）≥0.令V（z0，y0）=μ，則式（10）可改寫為

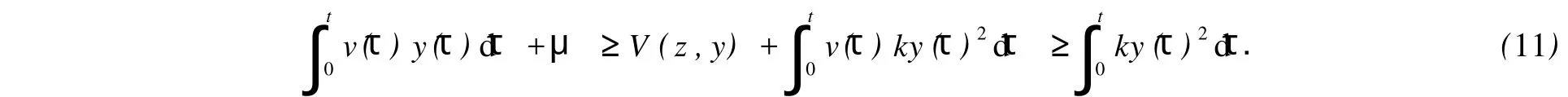
因此，由定義1可知，系統（4）為無源系統.

2 基于無源控制的超混沌Chen系統的同步

Chen系統的動態微分方程［10］為

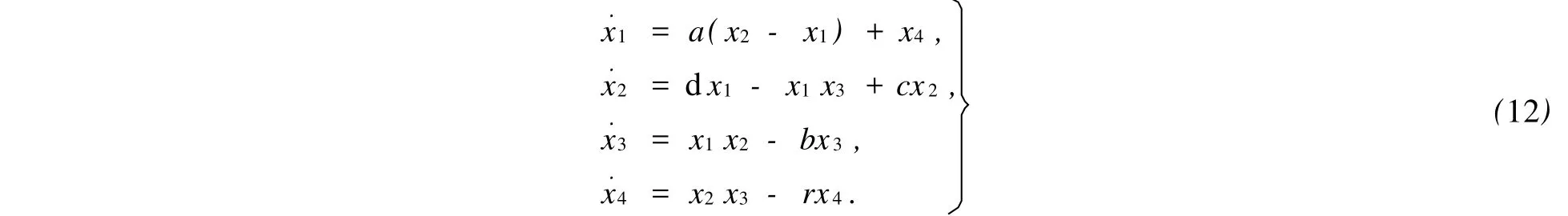
式中：xi（i=1，2，3，4）為系統的狀態量；a，b，c，d，r為系統參數.當a=35，b=3，c=12，d=7，0≤r≤0.085時，系統（12）表現出混沌特性；而當0.085≤r≤0.798時，系統（12）為超混沌系統.

假定系統（12）為驅動系統，其響應系統的動態微分方程為

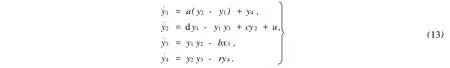
定義同步誤差e1=y1-x1，e2=y2-x2，e3=y3-x3，e4=y4-x4，且系統參數a，b，c，d，r未知.控制目標是在控制器u的作用下，使驅動系統（12）與響應系統（13）在不同初始條件下，其誤差滿足

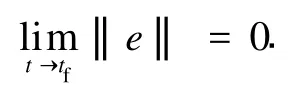
其中：tf為大于零的一時間值.兩超混沌系統的同步動態誤差方程為

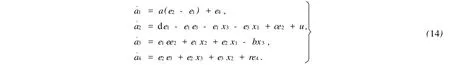
定理2 對于系統（2），根據定理1，當控制量u為

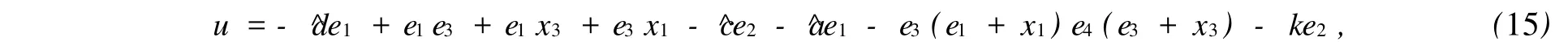
系統（14）將漸近穩定于狀態空間原點，即系統（12）與系統（13）將達到完全同步.式（15）中：^a，^c，^d分別為系統參數a，c，d的估計值，且其自適應更新律為

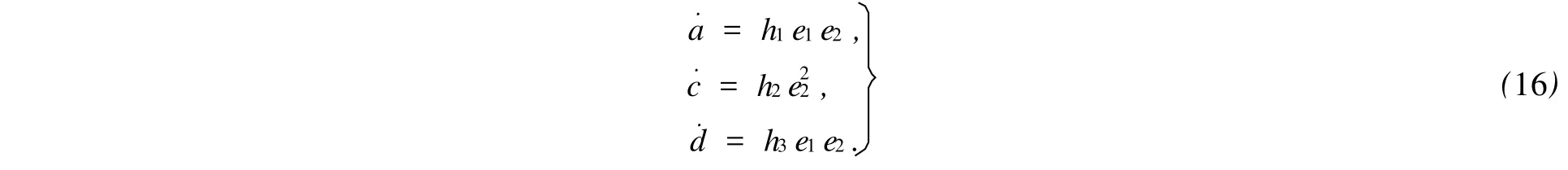
式（16）中：hi（i=1，2，3）為任意大于0的常數.

注1 由于控制器u只與系統參數a，c，d有關，而與b，r無關，因此只需估計參數a，c，d即可.

證明 令z1=e1，z2=e3，z3=e4，y=e2，則動態誤差方程（14）可改寫為

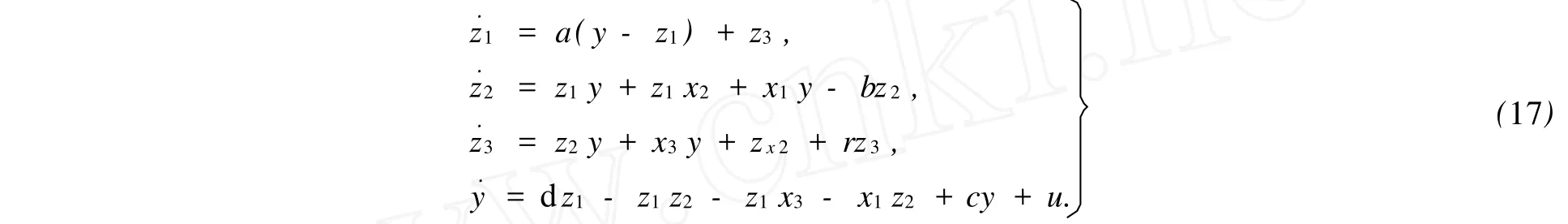
將式（17）改寫成式（4）的形式，則有

由定義2可知，系統（17）為最小相位系統.取系統（17）的Lyapunov函數為

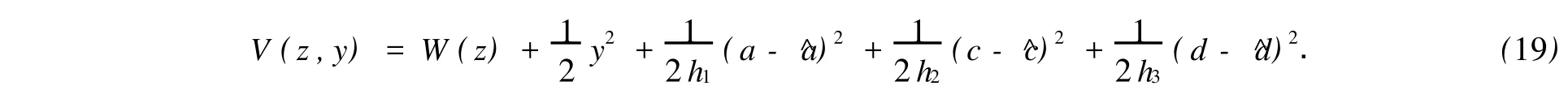
兩邊求導后可得

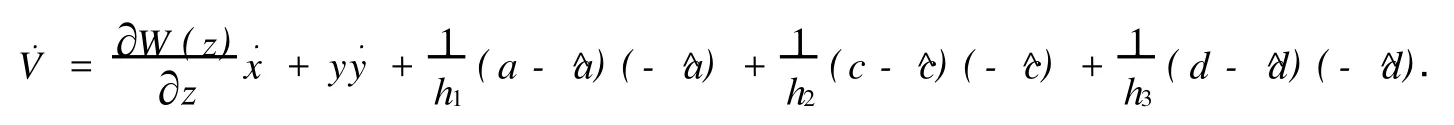
聯立式（15），（16），（17），可得

因此，由定理1可知，系統（17）為無源系統.證畢.

3 數值仿真

令驅動系統（12）各狀態變量的初始值［x1（0），x2（0），x3（0），x4（0）］=［0.5，0.5，0.5，0.5］；響應系統（13）狀態量的初始值［y1（0），y2（0），y3（0），y4（0）］=［1，1，1，1］；系統的動態誤差初始值為［0.5，0.5，0.5，0.5］.由于驅動與響應系統均為超混沌Chen系統，選取其系統參數的估計初值為（0）=1，（0）=1，（0）=1，設計參數h1=5，h2=7，h3=9，k=5.

為了便于比較，在t=10s時，響應系統（13）才加入控制器u.驅動系統和響應系統的同步輸出及誤差曲線，分別如圖1，2所示.由圖2可知，驅動系統（12）與響應系統（13）在控制器u的作用下很快達到同步，其誤差快速趨于零，即兩系統很快達到完全同步.

系統的參數a，c，d的估計值（P）曲線，如圖3所示.從圖3可知，隨著時間的推移，參數a，c，d的估計也逐漸收斂于某一常數值.

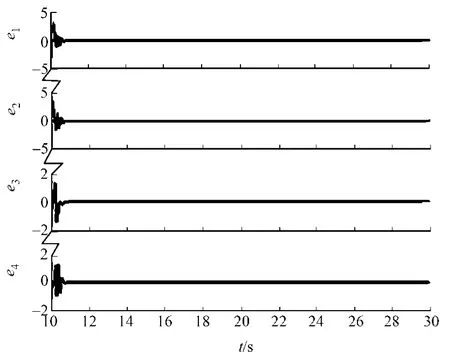
圖2 系統同步誤差曲線Fig.2 Curve of system synchronization error

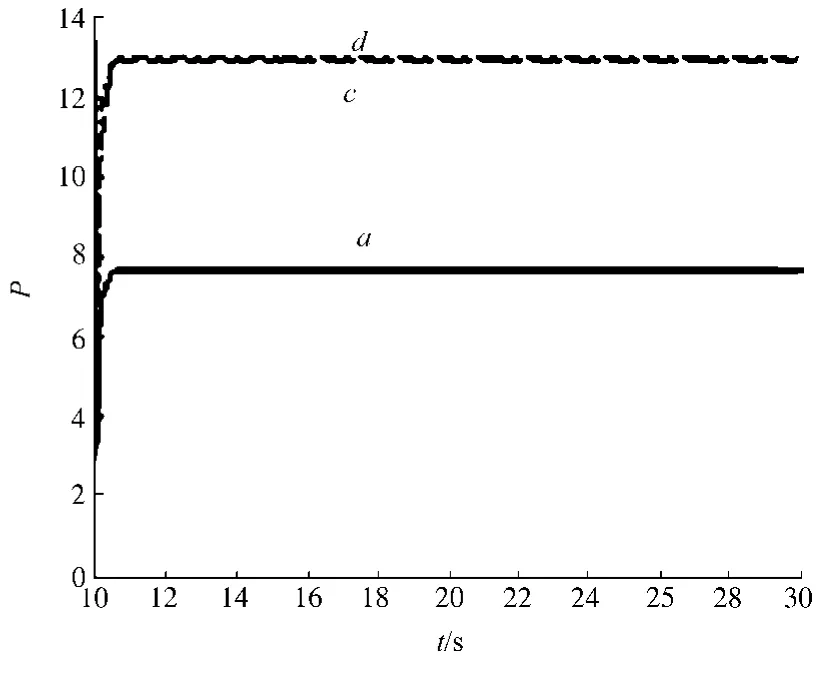
圖3 系統參數的估計值曲線Fig.3 Curve about estimation value for system parameters

4 結束語

提出一種基于無源控制的方法實現，具有參數不確定性超混沌Chen系統的同步.通過自適應控制在線估計系統的參數，設計一個自適應控制器使系統的同步動態誤差方程為無源系統.根據無源控制理論，將動態誤差系統穩定到零平衡點，即實現兩Chen系統完全同步.采用無源控制設計的控制器簡單明了，其物理意義更為明顯.

［1］PARKJ H.Adaptive synchronization of hyperchaotic Chen system with uncertain parameters［J］.Chaos，Solitons＆ Fractals，2005，26（3）：959-964.

［2］WANG Bo，WEN Guang-jun.On the synchronization of a class of chaotic systems based on backstepping method［J］.Physics Letters（A），2007，370（1）：35-39.

［3］HUANG Li-lian，FENG Ru-peng，WANG Mao.Synchronization of uncertain chaotic systems with perturbation based on variable structure control［J］.Physics Letters（A），2006，350（3/4）：197-200.

［4］CHEN H S.Global chaos synchronization of new chaotic systems via nonlinear control［J］.Chaos，Solitons＆Fractals，2005，23（4）：1245-1251.

［5］ZHANG Hao，MA Xi-kui.Synchronization of uncertain chaotic systems with parameters perturbation via active control［J］.Chaos，Solitons＆Fractals，2004，21（1）：39-47.

［6］CHEN F X，ZHANG W D.LMI criteria for robust chaos synchronization of a class of chaotic systems［J］.Nonlinear Analysis，2007，67（12）：3384-3393.

［7］LIN W.Feedback stabilization of general nonlinear control systems：A passive system approach［J］.Systems＆Control Letters，1995，25（1）：41-52.

［8］YU Wen.Passive equivalence of chaos in Lorenz system［J］.IEEE Transactions on Circuits and Systems（Ⅰ）：Fundamental Theory and Applications，1999，46（7）：876-878.

［9］BYRNES C I，ISIDORI A，WILL EMS J C.Passivity，feedback equivalence，and the global stabilization ofminimum phase nonlinear systems［J］.IEEE Transactions on Automatic Control，1991，36（11）：1228-1240.

［10］LI Y X，TANG W K S，CHEN G R.Generating hyperchaos via state feedback control［J］.International Journal of Bifurcation and Chaos in Applied Sciences and Engineering，2005，15（10）：3367-3375.

Adaptive Synchronization of Hyperchaotic Chen Systems via Passive Control

FU Gui-yuan，LI Zhong-shen
（College of Mechanical Engineering and Automation，Huaqiao University，Quanzhou 362021，China）

Under different initial conditions，a control method based on passive control is proposed to achieve the adaptive synchronization of two hyperchaotic systems with uncertain parameters.The system parameters are estimated by introducing adaptive control，and an adaptive passive controller is designed to transfer the synchronization erroneous equation into a passive system.In terms of the passivity theory，the dynamic erroneous equation can be stable on the original point of the state space，namely，the two hyperchaotic systems can be completely synchronized.The simulation results have proven the simplicity and effectiveness of the designed controller.

hyperchaotic Chen system；synchronization；passive control；adaptive control

TP 273

A

1000-5013（2010）04-0378-05

（責任編輯：黃仲一 英文審校：鄭亞青）

2009-10-21

李鐘慎（1971-），男，教授，主要從事最優控制、時滯系統的控制和抗飽和控制的研究.E-mail：lzscyw@hqu.edu.cn.

福建省自然科學基金計劃資助項目（E0710018）