Schrodinger方程的數(shù)值解

張子珍，呂仕儒

(山西大同大學(xué)物理與電子科學(xué)學(xué)院，山西大同 037009）

Schrodinger方程的數(shù)值解

張子珍，呂仕儒

(山西大同大學(xué)物理與電子科學(xué)學(xué)院，山西大同 037009）

利用實穩(wěn)定方法,借助Fortran程序求解薛定諤方程的束縛態(tài)問題.以諧振子勢為例,并與解析解進行比較,得到了滿意的結(jié)果.為求解薛定諤方程提供了一種較簡單的方法.

薛定諤方程 束縛態(tài) 解析解 數(shù)值解

微觀粒子的量子態(tài)用波函數(shù)來描述,波函數(shù)隨時間變化的方程就是Schrodinger方程,Schrodinger方程是量子力學(xué)中最基本的方程,其地位與Newton方程在經(jīng)典力學(xué)中的地位相當(dāng).在諧振子勢、方勢阱等勢場作用下,從數(shù)學(xué)上找出Schrodinger方程的解析解比較困難,對較復(fù)雜的勢如woods-Saxon作用下,幾乎無法求出Schrodinger的解析解.為了解決此問題,本文利用Fortran語言,求Schrodinger方程的數(shù)值解.利用實穩(wěn)定方法來找出Schrodinger方程的束縛態(tài),并將結(jié)果與解析解進行比較.

1 Schrodinger方程的引入

與具有一定能量E及動量p→的粒子相聯(lián)系的波是平面單色波,其表達式是

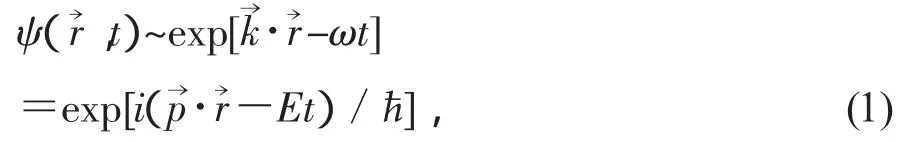
將上式對時間及坐標(biāo)求導(dǎo),并利用自由粒子的能量動量關(guān)系E=p2/2m,可得

假設(shè)勢場V中不顯含t,方程(4)可以用分離變量法求其特解,令ψ(r→,t)=ψ(r→)f（t）,代入(4)式,分離變量,得

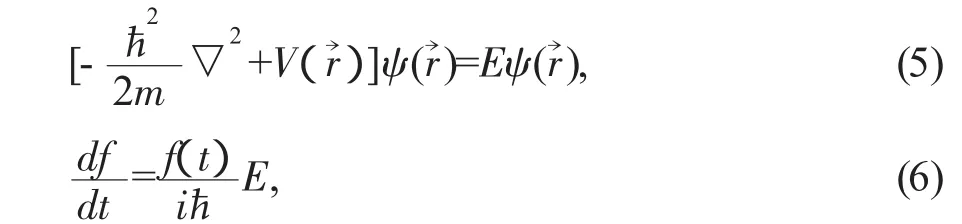
其中E是分離變量時引入的常數(shù).方程(4)的解是

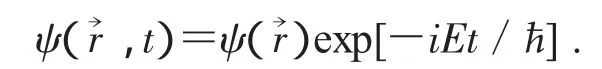
(5)式就是定態(tài)Schrodinger方程.

2 定態(tài)Schrodinger方程的解

2.1 在不同勢場作用下的解析解

2.1.1 諧振子勢

在一維諧振子勢下,Schrodinger方程變?yōu)?/p>

2.1.2 無限深方勢阱

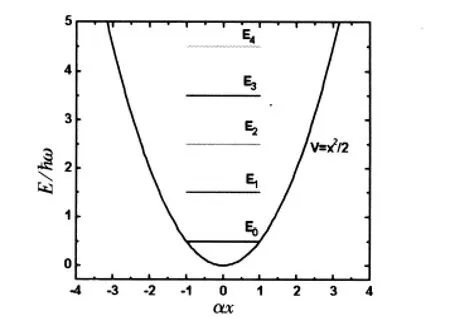
圖1 勢能曲線及解析求解得到的能級

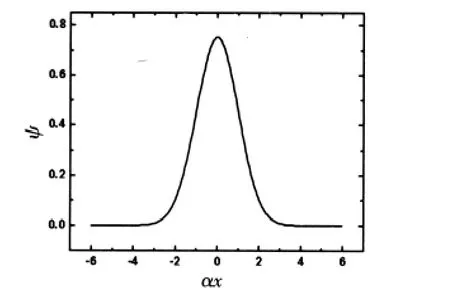
圖2 解析求解得到的零級波函數(shù)

在勢阱外,波函數(shù)為0,且

在求解過程中,得出其能量的本征值及本征函數(shù)分別為

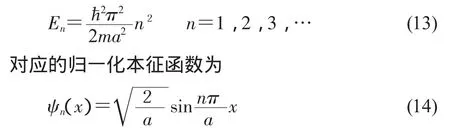
2.2 Schrodinger方程的數(shù)值解

2.2.1 坐標(biāo)空間的實穩(wěn)定方法

實穩(wěn)定方法是通過基展開的方法進行求解.在分立能區(qū),各本征態(tài)(束縛態(tài))的能量不會隨基空間的維數(shù)而改變;而在連續(xù)能區(qū),本征態(tài)的能量多數(shù)會隨著基空間維數(shù)的增加而逐漸降低,這些態(tài)對應(yīng)于散射態(tài);還有一些本征態(tài)能量隨基空間維數(shù)的增加會出現(xiàn)一個平臺,這些態(tài)對應(yīng)于共振態(tài)[2].束縛態(tài)的問題也可以在坐標(biāo)空間(離散的空間格點上)求解.通過改變坐標(biāo)空間的大小,可以得到本征能量隨格點數(shù)的變化關(guān)系.與基展開的方法類似,能量不隨坐標(biāo)空間格點數(shù)而改變的態(tài)就對應(yīng)于束縛態(tài)[3].

2.2.2 數(shù)值求解過程

1)給定初始能量,兩端初始波函數(shù)及其一階導(dǎo)數(shù)值.

2)通過Runge-Kutta[4]方法向match點推近.

3)利用match點波函數(shù)是否光滑對接及節(jié)點數(shù)判斷初始能量是否合適.

4)若節(jié)點數(shù)符合,波函數(shù)光滑對接,歸一化波函數(shù)之后輸出計算結(jié)果.

5)若節(jié)點數(shù)不符,則改變能量初值,重新進行計算,直到求得本征能量[5].

2.2.3 數(shù)值計算結(jié)果

1)諧振子勢.V（x）＝mω2x2/2,圖3～6分別給數(shù)值計算得到的能級及其波函數(shù).計算中均采用自然單位制m=ω=?=1.

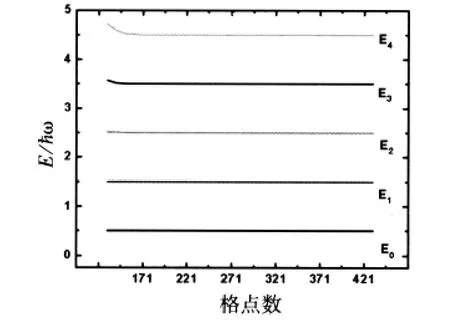
圖3 諧振子勢的能級隨格點數(shù)的變化規(guī)律

從圖3中可以看出,空間格點數(shù)從171增加到421時,各級諧振子的能量沒有發(fā)生任何變化,所以這些態(tài)對應(yīng)于束縛態(tài),它們的能級分別是0.5,1.5, 2.5,3.5,4.5?ω等.與解析求解得到的結(jié)果相當(dāng)吻合.

從圖4、圖5、圖6可以看出數(shù)值求解得到的波函數(shù)與解析求解得到的各級波函數(shù)也是完全一致的.

2)有限深方勢阱.

以下面有限深方勢阱為例來進行數(shù)值求解:

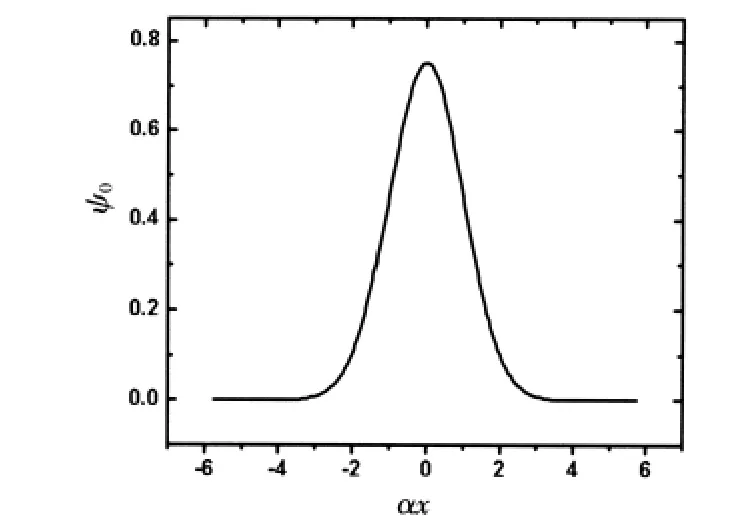
圖4 諧振子勢的第零級波函數(shù)

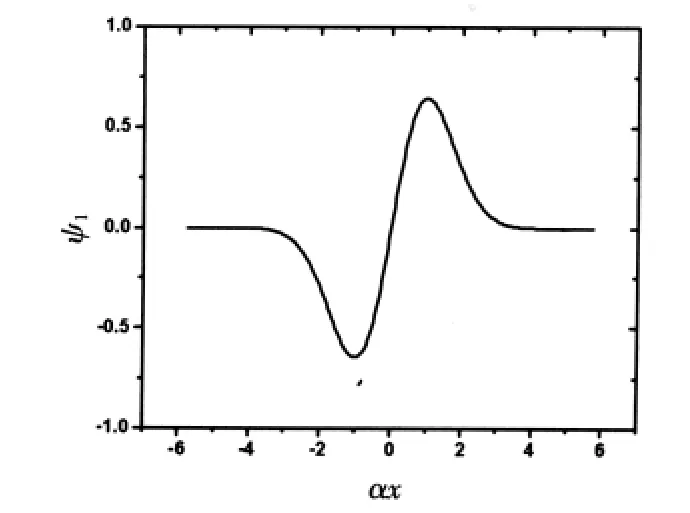
圖5 諧振子勢的第一級波函數(shù)

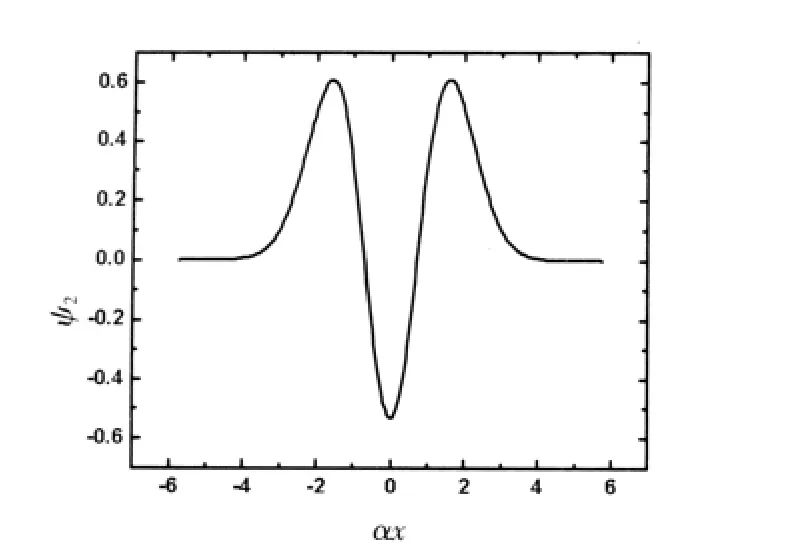
圖6 諧振子勢的第二級波函數(shù)

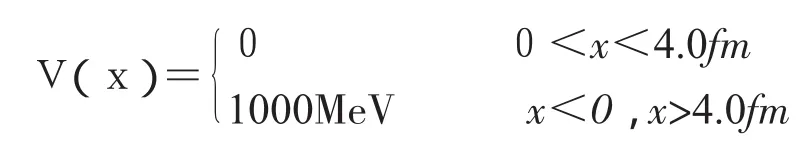
當(dāng)空間格點數(shù)從171變到571時,對應(yīng)于一些態(tài),它們的能量不隨格點數(shù)變化而變化,這些態(tài)就是束縛態(tài),它們的能級如下(單位是MeV):

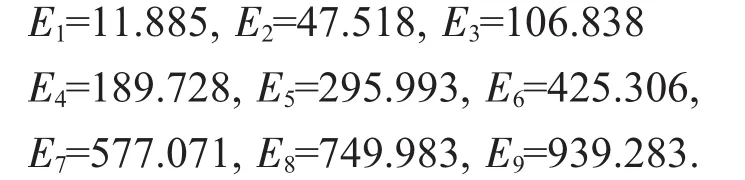
對數(shù)值求解得到的這些能級進行分析,發(fā)現(xiàn)隨著能級的升高,能級的間隔逐漸加大.而且各能級仍保持與量子數(shù)n2成正比的關(guān)系.

數(shù)值求解得到的與不同能級對應(yīng)的波函數(shù)如下:

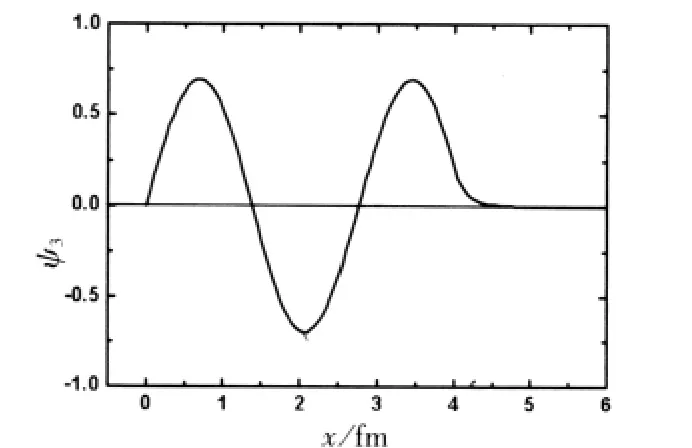
圖7 方勢阱的第三級波函數(shù)

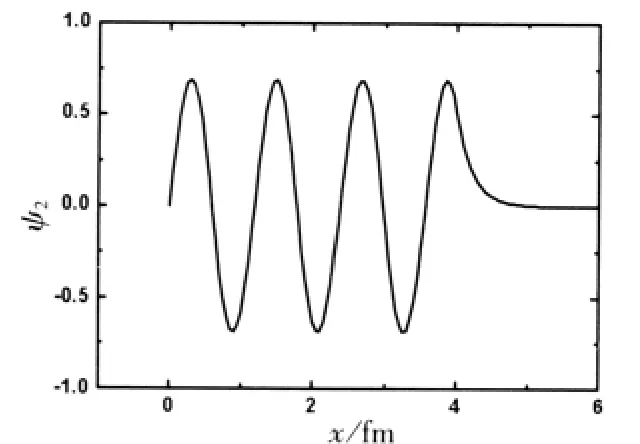
圖8 方勢阱的第七級波函數(shù)

從圖7～9可以看出,數(shù)值求解得到的各級波函數(shù)的節(jié)點數(shù)比它的級數(shù)剛好少一,這與無限深方勢阱的情況完全對應(yīng)。

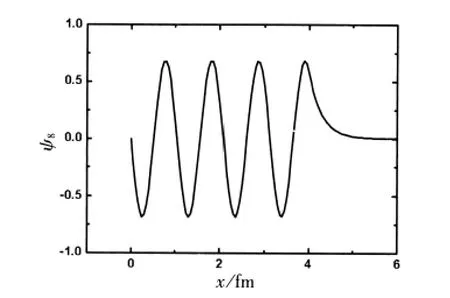
圖9 方勢阱的第八級波函數(shù)

2.3 兩種解的比較

對比在諧振子勢作用下的能級,圖1是解析求解得到的能級,而圖3是數(shù)值求解得到的能級,兩圖均采用自然單位制,從這兩圖中可以發(fā)現(xiàn),兩種方法得到的結(jié)果完全相同.再看在諧振子勢作用下的波函數(shù),圖2是解析求解得到的第零級波函數(shù),而圖4是數(shù)值解得到的第零級波函數(shù),這兩條圖線也完全一致.實際上其它級波函數(shù)也是完全一致的,本文中沒必要一一列出.圖5和圖6是數(shù)值求解得到的諧振子勢作用下的第一級和第二級波函數(shù).在有限深方勢阱作用下數(shù)值求解得到能級已給出,圖7～9是對應(yīng)的波函數(shù).從以上的分析可見,數(shù)值解與解析解得到的結(jié)論完全一致.而數(shù)值解最大的優(yōu)點在于只要編好Schrodinger方程解的程序,在不同勢場下求解時只要把勢場換一下問題就可迎刃而解,具有方便、快捷而且準(zhǔn)確的特點.

3 展望

本文利用實穩(wěn)定方法求出一維Schrodinger方程在不同勢作用下的束縛態(tài)問題,對三維Schrodinger方程的求解程序,以及散射態(tài)及共振態(tài)問題是下一步工作的方向.當(dāng)然實穩(wěn)定方法只是求解Schrodinger方程的一種方法,還可以考慮用其它不同的方法對Schrodinger方程進行數(shù)值求解.

[1]曾謹(jǐn)言.量子力學(xué)（卷Ⅰ）[M].北京:科學(xué)出版社,1995：101-105.

[2]Hazi A U,Taylor H S.Stabilization Method of Calculating Resonance Energies：Model Problem[J].Phys RevA，1970，1：1109.

[3]張力，周善貴，孟杰.單粒子共振態(tài)的實穩(wěn)定方法研究[J].物理學(xué)報，2007，56（7）：38－39.

[4]黃云清，舒適，陳艷萍，等.數(shù)值計算方法[M].北京：科學(xué)出版社，2009：274－286.

[5]劉衛(wèi)國，蔡旭暉.FORTRAN 90程序設(shè)計教程[M].北京：北京郵電大學(xué)出版社，2003.

N umerical S olution of Schrodinger E quation

ZHANG Zi-zhen，LU Shi－ru
(School of Mathematics and Computer Science,Shan x iDa t ong University,Da t ong Shan x i，037009)

The numerical solutions of schrodinger equation are studied by real stabilization.Taking Harmonic Oscillator potential as an example,the results are also compared with analytical solutions,and satatisfy agreements are found.We provide a new way to solve schrodinger equation.

schrodinger equation;bound state;analytical solution;numerical solution

O 41

A

〔編輯 李海〕

1674－0874（2010）02－0022－03

2009-03-26

張子珍(1965-),女,山西陽高人,教授,研究方向:原子核結(jié)構(gòu)理論.