波浪在緩變海底上傳播的一個簡單數學模型

彭延建，劉應中，時鐘

（上海交通大學船舶海洋與建筑工程學院 海洋工程國家重點實驗室 港口與海岸工程系，上海 200030）

波浪在緩變海底上傳播的一個簡單數學模型

彭延建，劉應中，時鐘

（上海交通大學船舶海洋與建筑工程學院 海洋工程國家重點實驗室 港口與海岸工程系，上海 200030）

基于Liu和Shi（2008）的波浪勢函數零階、一階近似解，采用四階龍格-庫塔法，對緩變海底上一維波浪傳播理論模型進行了數值求解，并對波浪在定常坡度的斜坡地形、雙曲正切地形為例的傳播、變形進行了研究。為了更逼真地描述流體質點的波動特性，將在Euler坐標系下得到的解轉換至Lagrange坐標下的解，并繪制Lagrange坐標下坡度為0.2的海灘上的一個波周期內臨近破碎前的波形的詳細變化過程。此外，計算得到了變水深區域波浪速度勢以及自由面的分布，并與Athanassoulis and Belibassakis[34]的結果進行了對比，表明本文模型比保留了六個瞬息項的后者更有效。

波浪傳播；緩變海底；波形；攝動

波浪在向近岸傳播的過程中，因為受到海岸地形等因素的影響，會發生淺化、折射與繞射；波況也隨之變化，如：波長變短、波高先減小后增大、波速變慢、波向也會趨于與岸線垂直。波浪在緩變海底上傳播的研究，對物理海洋學、海岸動力學等有科學意義，同時，對港口航道海岸工程亦有實踐意義。

對波浪折射、繞射的研究最初來源于光學的啟發，Penny和Price[1]指出光學中經典的Sommerfeld[2]解也是波浪繞射問題的解。利用反射原理，Lewy[3]得到了波浪在變水深傳播的控制方程和解析解，但是其結果在近岸處發生奇異，波幅無限大，與實際物理現象不符。基于光學中的折射理論，Arthur[4]以及Munk和Arthur[5]根據Fermat原理(Fermat principle)，推導出特征線方程和其常微分方程形式，后來射線理論成為求解波浪折射的主要方法。自20世紀1950年代起，波浪的傳播進一步引起科學家和工程師的關注，得到了一些理論解析解。當然，有關波浪折射與繞射的數值方法也得到發展[6-12]。以下簡要地對理論解析解的研究做一綜述。

在線性化自由邊界條件下，Eckart[13]提出描述波浪從深水向淺水傳播的數學模型，對于斜坡地形特例，解出了級數形式的解析解。同樣在線性化自由邊界條件下，Peters[14]和Roseau[15]推導得到積分形式的解析解。對于波浪垂直入射坡度為 的緩坡的問題，Biesel[16]將波浪的勢函數以坡度為參數攝動展開，提出一個一階的勢函數的解析解，和波幅變化的表達式。利用波浪射線理論和波能守恒理論，Battjes[17]推導出波浪在緩坡上傳播的勢函數的解析表達式。對于等深線平直的情形，Mei和LeMehaute[18]利用WKB (Wentzel-Kramers-Brillouin approximation)法漸進展開，得到波浪勢函數的一階解和二階解。對于不同的波幅水深比，Mei等[19]給出一組擬線性雙曲型方程，描述波浪的繞射。利用攝動法，以波陡為攝動參數，Chu和Mei[20]推導得到波浪速度勢函數的解析解，此解析解含有坡度的一階參數 ，能夠反映床底坡度對波動解的影響。Liu和Dingemans[21]針對斜坡底床上的前進波列，利用多重尺度法，將水平面上的坐標分為快變變量和慢變變量，推導出包含弱非線性及底床坡度效應的Ο(ε2)階波動勢函數的解，此解可以認為是對Chu和Mei[20]的修正。Massel[22]以Galerkin的特征函數法推導出一個緩坡方程，其中保留了地形變化的高階量，因此，對于床底之微小變形造成的反射有良好反應。基于線性自由表面邊界條件，為了反映床底坡度效應，Chen等[23]將波動場以床底坡度

攝動展開，求得包含底床斜坡效應的前進波勢函數的解析解。Chen等[24]通過攝動展開求得非線性參數到3階、坡度到1階的勢函數解析解，并轉換至Lagrange坐標系下。Hsu等[25]將Chen等[23]提出的包含底床斜坡效應的前進波勢能函數的解析解，加以處理后，代入沿水深積分的方程，得到一種新型的補充緩坡方程(complementary mild-slope equation)。

鑒于Biesel[16]沒有給出具體的推導過程，文圣常、余宙文[26]重新推導，給出了一個級數形式的波幅解。基于射線理論，李德筠、沈國光[27]提出了一種解決射線相交的簡便方法。運用水波Hamilton變分原理，黃虎[28]得到一個近岸不平海底的緩坡方程，其中考慮了水深一般變化的二階效應。對波浪折射繞射問題的研究，大陸學者多集中于對緩坡方程和Boussinesq方程的理論改進和數值方法研究[29-32]，對用理論解析解決波浪折射繞射問題研究可能還是相對較少。

盡管國內、國外對波浪傳播進行了大量的研究，但由于波浪傳播本身物理過程的復雜性，一些基本過程仍需研究和探討。基于線性波浪理論，利用攝動理論中的多重尺度法，以坡度 為小參數，Liu和Shi[33]推導出波幅方程，以及一階勢函數的解析解，但未對模型實現與驗證。

本文的目的：(1)將Liu和Shi[33]中的理論模型加以實現；(2)采用此模型描述流體質點的波動特性，即Lagrange坐標下的一個波周期內臨近破碎前的波形的變化過程；(3)通過與文獻Athanassoulis和Belibassakis[34]的結果進行比較，以驗證本模型的有效性。

1 數學模型

本文的數學模型理論部分也可參見Liu和Shi[33]，為了使此中文文稿具完整性，故將Liu和Shi[33]中理論模型在此做簡要地介紹。以笛卡爾坐標系為參考坐標，水平 軸位于靜水面，與岸線的交點為坐標原點(0,0)，指向外海，z軸垂直向上，如圖1所示。

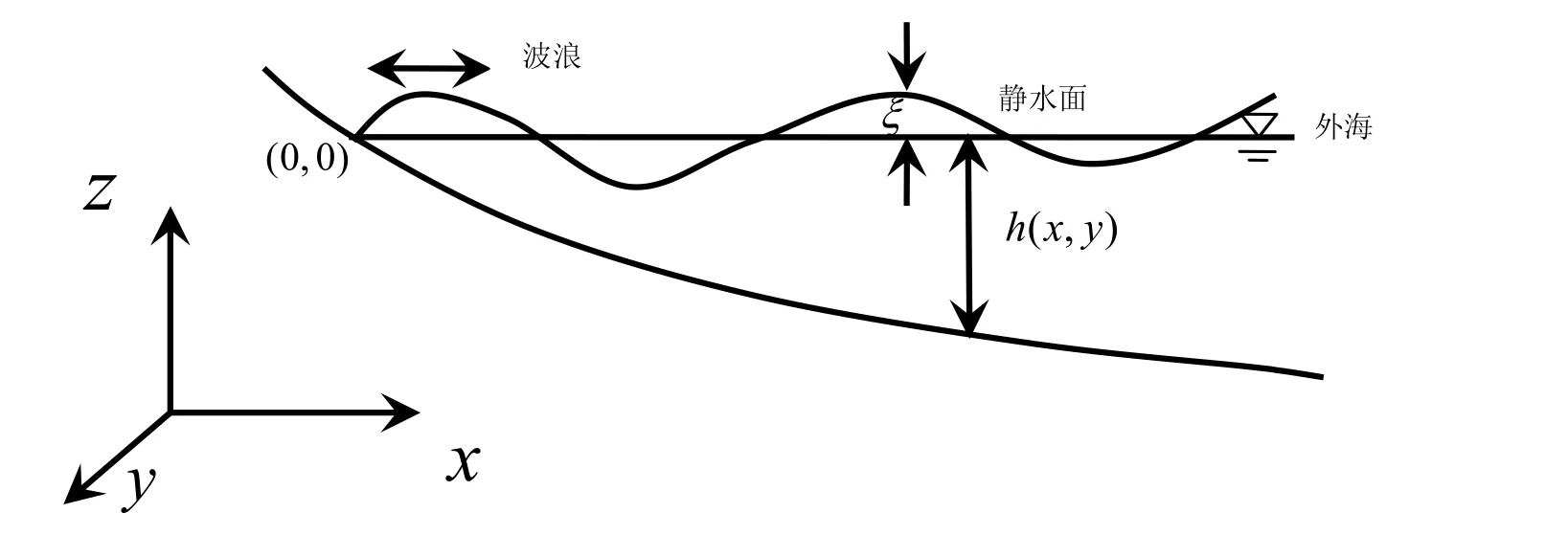
圖1 波浪在不平坦底床傳播示意圖及笛卡爾坐標系Fig. 1 Sketch of wave propagation over an uneven bottom and the Cartesian coordinate system

數學模型的推導基于經典的線性波理論和攝動理論中的多重尺度法。假設外海入射波為單色波，無窮遠處水深不變，比如z=?h0，h0是常數。其速度勢函數如下：

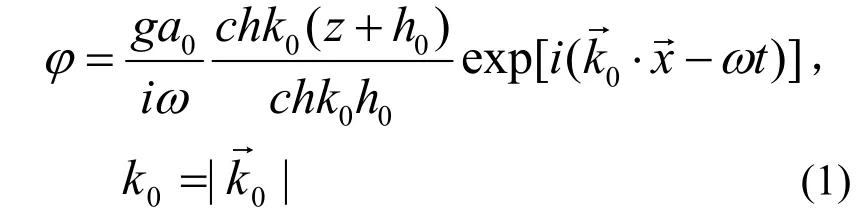
波浪的相對頻率 與波數k0滿足色散關系式：

假設底床為緩變海底，|?h|/kh 為一小量 ，即在一個波長范圍內，h的變化很小。

1.1 零階近似解

零階解的推導與在常水深條件下的解具有相同的形式，但同樣適用于水深緩變的情況，它的解為：

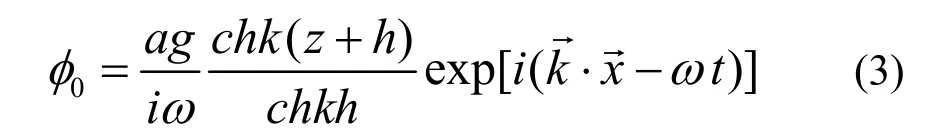
對應的波面函數為：

零階解是滿足底部邊界條件的。根據自由表面邊界條件，得到色散關系式：

在無窮遠處，

可求得每個水深點的k1和k2。

1.2 一價近似解

在式(3)中，對x求偏導：

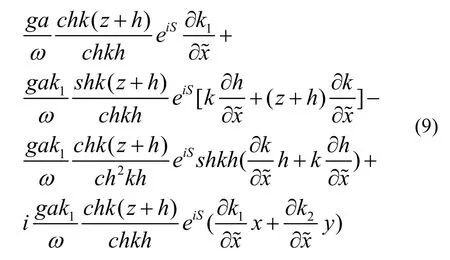
一階近似解的方程和條件變為：

以上推導中的參數A、B、C、C0、C1和C2均為關于水平尺度(x, y)的函數。假設一階解的形式為：

將式(11)代入式(10a)，比較等式兩邊的系數，得到：

容易驗證這個解是滿足底部邊界條件的。結合色散關系式，將式(11)代入式(10b),自由表面邊界條件為：

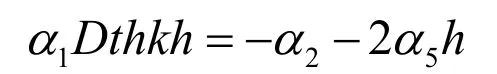
波幅函數確定后，勢函數的解析解也就隨之確定：

波浪場的流速具有以下形式：

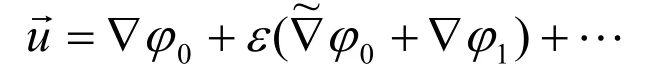
自由面的表達式為：

如果y方向上地形沒有變化，來波正向入射，波幅的變化是一維的，式(12)變為：

積分后得到：

其中，a0為初始波幅，也即x～→∞時入射波的波幅。

2 計算方法

對于h=x的特殊算例，在物理尺度下實際是坡度為 的斜坡，波幅的變化已經給出顯式解。如果坡度不是常數的緩坡，波幅方程轉化為一個常微分方程，整理后得：

可采用四階龍格-庫塔 (Runge-Kutta)方法計算。波幅求出后，勢函數、波形等物理量，在1.2節的推導中，已有顯式的解析解，代入波幅即得到速度勢和波形。

根據Mason[35]的試驗證實，由Lagrange坐標系表示的波形能夠更好地保持波動的真實性。為了采用本模型盡可能更好地保持波形的真實性，將以上方程求得的波形解轉化為Lagrange坐標系下的解。下面將本文的解轉換為Lagrange坐標系的解。根據u, w的表達式，求得起始位置在(x, y)處的流體質點水平方向和垂直方向位移(X, Z)分別為：

Lagrange坐標系的波形函數如下所示：

3 結果與討論

對于坡度為常數的情形，采用本文方法所得的波幅，即式(16)，與Biesel[16]的結果在形式上是相同的，所以本文模型包含了Biesel[16]的解。圖2為Lagrange坐標系下波浪入射到斜坡時，一個波周期內波形連續變化的過程。起始的時間為t=0，連續兩個相位之間的時間差為T/8。由圖2中可以看出，波浪傳播到海岸時，波浪尾部逐漸拉長，有變平滑的趨勢，而波浪前緣變得越來越陡，在6T/8時刻左右，波浪臨近破碎，波峰變得很尖，這與真實的波浪是吻合的。值得一提的是，圖2中，7T/8時刻及T時刻近岸處波浪實際已破碎，破碎帶內本模型已不再適用。

為了更清晰地觀察波峰臨近破碎的情況，在模擬過程中，Δt取為T/48，模擬得出連續6個連續時刻的波形，從中能夠清楚地觀察到波峰變陡并逐漸向內卷曲的過程(圖3)。

值得一提的是，以波陡和底床坡度為小參數，Chen等[24]推導得到一個應用于傾斜海底的考慮非線性效應的勢函數的解析解，坡度展開到二階，并同樣轉化至Lagrange坐標系。按照Chen等[24]的結論，在入射波陡為0.05、坡度為0.2的條件下，破碎形態應為卷波型(Plunging breaker)。本模型所得到的圖3結果與Chen等[24]結論是吻合的。

此外，本文還研究相同波浪條件下不同坡度情況的正向傳播，以進一步說明理論模型的適用性。限于篇幅，圖從略，結果簡述如下：本文選取0.01、0.02、0.05和0.10四個坡度進行比較，外海波浪正向入射，深海波陡k0a0=0.05、波周期T=1 s。從四種不同坡度下波形的變化圖可以看出，它們與Biesel[16]的結果非常接近。相比零階解，一階解的波幅和相位均有所變化。波浪在坡度較緩(0.01, 0.02)的底床上波高先增大，波長變短，并且破碎早于較陡的底床。在坡度為0.05和0.10的情形中，波浪在非常靠近岸邊的地方才開始出現變形效應，波高增大，波長變短。分析其原因，可能由于在坡度較大的情況下，從外海入射邊界算起，在很長的一段距離內kh＞ ，水深為深水條件，波長等于

2/2 gT；而我們假設波浪傳播過程中周期是不變的，因而，波長也不變。其中的原理可以理解為：底床坡度大，水深較深，所以，海底底床對波浪的影響小。

需說明的是，如圖2所示，雖然本文模型可以較好地描述波浪卷破前的形態，但是，模型是否可以得到波浪“坍破”和“涌破”前形態仍須進一步的研究。

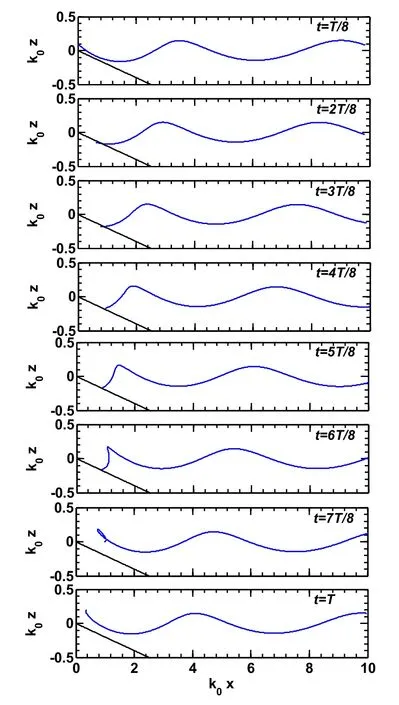
圖2 波浪在坡度為0.2的海灘上傳播中一個波周期內波形連續變化和破碎前的過程，時間間隔為T/8Fig. 2 Time series of modeled wave profiles prior to breaking on a beach over one wave period T at a slope 0.2 and the time interval of T/8

為了進一步了解本模型的適用性，現在將模型用于斜坡斜率非恒定的地形。現將本文模型也應用于Massel[22]的雙曲正切函數地形，該地形的水深函數的形式為：

其中h1=6m，h3=2m，緩坡海底的長度b=20m。波浪正向入射，波高1.0m，周期T=3.14s。

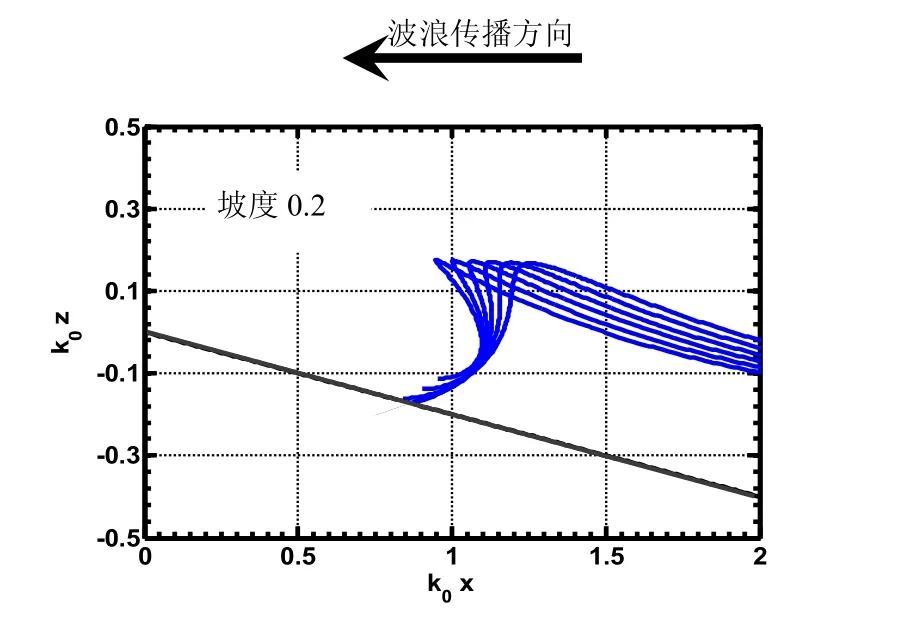
圖3 模擬得到的海灘上 t=6T/8時刻附近波浪臨近破碎時波形連續變化的詳細圖，坡度為0.2，時間間隔為T/48Fig. 3 Details of modeled successive wave profiles prior to breaking around t=6T/8 on a beach at a slope of 0.2 and the time interval of T/48.

為了驗證求解波幅方程式(14)的數值方法的合理性，首先，將本文模型算得的波形與Dean和Dalrymple[36]中基于波能守恒原則的淺化公式(4.117)的結果進行對比(圖4)，本文模擬得到的波形，與淺化公式結果是非常吻合的。

其次，本文模擬得到了在變水深區域波浪場勢函數的解，如圖5 (I)所示。Athanassoulis和Belibassakis[34]中速度勢的表達式為：

而在本文速度勢的表達式中虛數單位i在分母上，注意圖5(I)中的實部其實是式(13)的虛部。Athanassoulis和Belibassakis[34]的結果如圖5 (II)中所示。圖5表明：

(i) 本文速度勢分布結果與Athanassoulis和Belibassakis[34]的結果是很相似的，而且一階解比零階解更為接近ER的結果，尤其是速度勢的虛部。

(ii) 雖然在精確度上尚不如ER模型，但是Athanassoulis和Belibassakis[34]保留了衰減項(Evanescent mode)，或稱作非傳播項(Non-propagating mode)，這些局部項包含了波浪的繞射和反射作用。

圖4 0到20m斷面內t=0.6s時刻本文模型計算得到的波形(實線)與Dean 和Dalrymple[36]基于波能守恒原則的淺化公式(4.117)的結果(空心圓)的對比，對應的地形見圖5Fig. 4 Comparison of wave profiles at t=0.6s for a cross-section between 0 and 20m calculated by the present model (solid lines) and Dean and Dalrymple[36]shoaling equation (4.117) based on the conservation of wave energy (open circles). The corresponding bathymetry is shown in Fig. 5

(iii) 圖5 (II)所示ER模型的結果保留了7項局部項，而本文模型只對速度勢攝動展開到1階，并且不考慮繞射和反射，能達到圖5的相似程度，說明本文模型是較為有效的。

圖5 變水深區域波浪勢函數的等勢線以及自由面高度的對比，虛線代表零階解，實線代表一階解。注：(I) 本模型的結果: (A)為勢函數的實部；(B)為勢函數的虛部。(II) Athanassoulis and Belibassakis[34]的結果: (a)為勢函數的實部；(b)為勢函數的虛部。Fig. 5 Comparisons of equipotential lines of the wave potential function and free-surface elevation over variable bathymetry regions as obtained by the zero-order solution (dashed line) and 1st-order solution (solid line), respectively. Note that (I) the present model: (A) Real parts of the wave potential; and (B)Imaginary parts of the wave potential. (II) Athanassoulis and Belibassakis[34]: (a) Real parts of the wave potential; and (b) Imaginary parts of the wave potential.

4 結論與展望

本文初步研究結果可概括為以下幾點：

(i) 對于坡度為常數的斜坡特例，本文模型求解出顯式的波幅函數。將本文Euler坐標系下推導得到的波形解轉換至Lagrange坐標系后，結果顯示本文得到的一階解能夠呈現波動的特性。

(ii) 本文用于求解波幅方程的數值方法能夠得到較為精確的結果，所求得的一階解相比零階解更精確，表明本文模型同樣適用于坡度斜率有變化的情形。

(iii) 本文模型的不足之處是波動場勢函數的等勢線與海底底床不是處處垂直，如果在攝動展開過程中保留更高階項，上述不足或將得到改善。

綜上所述，本文模型可以認為是Biesel[16]解的擴展。不但收斂于Biesel[16]的解，而且本文模型可以適用于坡度變化的地形，并且具有較為滿意的精度。本文得到的解析解及數值解最好能夠與實測資料進行比對分析，這也是本項研究工作下一步應該努力的方向。顯然，本文的研究結果僅限于一維波浪傳播問題，今后，擬將本文模型應用到平面二維波浪傳播問題，屆時，可以嘗試著采用經典的試驗實測資料，對本模型進行對比分析。本文中所求解的問題都是簡化了的一維情形，即等深線是平行于海岸線的直線，水深只在波浪傳播方向上變化，波浪正向入射且傳播方向保持不變。針對于二維情形，水深在 和y方向上均有變化，波浪會發生折射與繞射，求解波幅方程的數值方法相比一維情形將復雜一些。更高階解的推導，以及二維問題波幅方程的數值求解和驗證，有待進一步的研究。

致謝：感謝史鋒巖從美國University of Delaware寄來文獻[16]。臺灣中山大學海洋環境及工程系陳陽益教授就坐標轉換問題給予了作者極大的幫助。

[1] Penny W G, Price A T. Diffraction of sea waves by breakwaters [J].Philosophical Transactions of the Royal Society London, 1944,A-244: 236–253.

[2] Sommerfeld A. Mathematische Theorie der Diffraction [J].Mathematische Annalen, 1896, 47: 317–374.

[3] Lewy H. Water waves on sloping beaches [J]. Bulletin of the American Mathematical Society, 1946, 52 (9): 737-775.

[4] Arthur R S. Refraction of water waves by islands and shoals with circular bottom contours [J]. Transactions American Geophysical Union, 1946, 27 (2): 168-177.

[5] Munk W H, Arthur R S. Wave intensity along a refracted ray [S]. In:Gravity Waves. U.S. National Bureau of Standards Circula, 1952:521: 95-108.

[6] Berkhoff J C W. Computation of combined refraction-diffraction [C].Proceedings of the 13th International Conference on Coastal Engineering, Vancouver, ASCE, 1977: 471-490.

[7] Ito Y, Tanimoto K. A method of numerical analysis of wave propagation: application to wave diffraction and refraction [C].Proceedings of the 13th International Conference on Coastal Engineering, Vancouver, ASCE, 1972: 503-522.

[8] Radder A C. On the parabolic equation method for water-wave propagation [J]. Journal of Fluid Mechanics, 1979, 95 (1): 159-176.

[9] Kirby J T. Higher-order approximations in the parabolic equation method for water waves [J]. Journal of Geophysical Research, 1986,91: 933-952.

[10] Panchang V G, Wei G, Pearce B R, Briggs M J. Numerical simulation of irregular wave propagation over shoal [J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 1990, 116(3):324-340.

[11] Li B. An evolution equation for water waves [J]. Coastal Engineering, 1994a, 23 (3-4): 215-225.

[12] Li B. A generalized conjugate gradient model for the mild slope equation [J]. Coastal Engineering, 1994b, 23 (3-4): 227-242.

[13] Eckart C. The propagation of gravity waves from deep to shallow water [S]. In: Gravity Waves. U.S. National Bureau of Standards Circular, 1952, 521: 165-173.

[14] Peters A S. Water waves over sloping beaches [J]. Communications on Pure and Applied Mathematics, 1952, 9: 443-493.

[15] Roseau M. Contribution à la théorie des ondes liguides de gravité en profondeur variable [J]. Publications Scientifique et Techniques du Ministère de l’ air. Paris, 1958: 275.

[16] Biesel F. Study of wave progression in water of gradually varying depth [S]. In: Gravity Waves. U.S. National Bureau of Standards Circular, 1952: 521: 243-253.

[17] Battjes J A. Refraction of water waves [J]. Journal of the Waterways,Harbors and Coastal Engineering Division ASCE, 1968, WW4:437-451.

[18] Mei C C, LeMehaute B. Note on the equations of long waves over an uneven bottom [J]. Journal of Geophysical Research, 1968, 71:393-400.

[19] Mei C C, Tlapa G A, Eagleson P S. An asymptotic theory for water waves on beaches of mild slope [J]. Journal of Geophysical Research, 1968, 73: 4555-4560.

[20] Chu V H, Mei C C. On slowly-varying Stokes waves [J]. Journal of Fluid Mechanics, 1970, 41: 873-887.

[21] Liu P L F, Dingemans M W. Derivation of the third-order evolution equations for weakly nonlinear water waves propagating over uneven bottoms [J]. Wave Motion, 1989, 11: 41-64.

[22] Massel S R. Extended refraction–diffraction equation for surface waves [J]. Coastal Engineering, 1993, 19: 97–126.

[23] Chen Y Y, Yang B D, Ou S H, Hsu J R C. Transformation of progressive waves propagating obliquely on gentle slope [J].Journal of Waterway, Port, Coastal, and Ocean Engineering, 2004,130 (4): 162-169.

[24] Chen Y-Y, Hwung H-H, Hsu H-C. Theoretical analysis of surface waves propagation on sloping bottoms: Part 1 [J]. Wave Motion,2005, 42 (4): 335-351.

[25] Hsu T W, Lin T Y, Wen C C, Ou S H. A complementary mild-slope equation derived using higher-order depth function for waves obliquely propagating on sloping bottom [J]. Physics of Fluids,2006, 18 (8): 087106-14.

[26] 文圣常, 余宙文. 海浪理論與計算原理 [M]. 北京: 科學出版社,1984: 662.

[27] 李德筠, 沈國光. 變深區淺水波的繞射和折射計算 [J]. 海洋學報, 1995, 17 (2): 106-116.

[28] 黃 虎. 波-流相互作用的緩坡方程及其波作用量守恒 [J]. 力學學報, 2005, 37 (5): 627-631.

[29] 鄭永紅, 夏 進. 近岸大區域水波數學模型及其數值求解 [J].海洋學報, 2000, 22 (5): 106-112.

[30] 李孟國, 時 鐘, 李文丹. 綜合考慮多種變形因素的近岸多向不規則波傳播數學模型_I_模型的建立 [J]. 水動力學研究與進展,2006, 21 (4): 444-451.

[31] 柳淑學, 孫 冰. 考慮邊界波浪方向的緩坡方程自適應求解模型[J]. 海洋工程, 2007, 25 (1): 35-44.

[32] 張洪生, 趙紅軍, 丁平興, 繆國平. 非均勻水流水域波浪的傳播變形 [J]. 力學學報, 2007, 39 (3): 325-333.

[33] Liu Y Z, Shi John Z. A theoretical formulation for wave propagations over uneven bottom [J]. Ocean Engineering, 2008, 35(3-4): 426-432.

[34] Athanassoulis G A, Belibassakis K A. A consistent coupled-mode theory for the propagation of small-amplitude water waves over variable bathymetry regions [J]. Journal of Fluid Mechanics, 1999,389: 275-301.

[35] Mason M A. A study of progressive oscillatory waves in water [R].U.S. Army Corps of Engineers, Beach Erosion Board, Technical Report No. 1, 1941.

[36] Dean R G, Dalrymple R A. Water Wave Mechanics for Engineers and Scientists [M]. World Scientific Publishing Co., Pte, Ltd., 1984:353.

A simple mathematical model of wave propagation over a gently sloping sea bottom

PENG Yan-jian, LIU Ying-zhong, SHI Zhong
(School of Naval Architecture, Ocean and Civil Engineering, The Shanghai Jiao Tong University, Shanghai 200030, China)

Based on the zero-order and first-order approximate solutions of the wave potential function in Liu and Shi[33], using the fourth-order Runge-Kutta method, the numerical solution has been made for the theoretical model of one-dimensional wave propagation over a gently sloping sea bottom in this paper. This paper also elucidates how waves propagate and deform over sloping bottom with a constant slope and hyperbolic tangent-shaped topography. To clearly depict the undulating motions of water particles, calculated solutions of the present model are transformed from the Euler coordinate system into the Lagrange coordinate system. Details of successive wave profiles prior to breaking on a beach at a slope of 0.2 over one wave period are plotted in the Lagrange coordinate system. Furthermore, the wave potential and free-surface elevation over the variable bathymetry regions are calculated by the present model and then compared with Athanassoulis and Belibassakis’[34]results. The present results are more efficient than the latter obtained by retaining six evanescent modes.

wave propagation; sloping sea bottom; wave profiles; perturbation

TV139.2

A

1001-6932(2010)03-0302-08

2010-01-20；

2010-04-16

國家自然科學基金 (水利科學50679040)、上海交通大學特聘教授基金(DP2009012)

彭延建 (1983－)，男，碩士研究生，研究波浪數值模擬。電子郵箱：pengyanjian@gmail.com

時鐘 (1965－)，男，教授。電子郵箱： zshi@sjtu.edu.cn