深水細長柔性立管渦激振動響應形式判定參數研究＊

張立武 陳偉民

(中國科學院力學研究所環境力學重點實驗室)

深水細長柔性立管渦激振動響應形式判定參數研究＊

張立武 陳偉民

(中國科學院力學研究所環境力學重點實驗室)

利用有限元數值模擬方法研究了深水細長柔性立管在正弦形式渦激升力作用下的動響應,并通過量綱分析結合函數擬合方式給出了判定立管渦激振動響應形式的無量綱參數的表達式和臨界值,該參數與系統阻尼(包括流體阻尼和結構阻尼)、結構模態階數及結構長度等有關。在實際海洋工程中,當設計或監測人員在預測立管的渦激振動響應時,可以先利用本文方法判定振動響應形式,然后根據響應形式選擇合適的預報模型。

深水 立管 渦激振動 響應形式 判定參數

水深增加,海洋平臺水下結構(如輸油立管、平臺的張力腿或系泊錨鏈等)的長度也會增加,而且幾何結構更為復雜,這時深水細長柔性立管渦激振動會表現出一些特有的復雜現象,例如多模態振動、寬帶隨機振動以及渦致行波(又稱VIW)等,從而給深海細長柔性立管渦激振動研究帶來了新的挑戰。近年來的研究結果表明,當立管的長徑比超過103量級時,渦激振動經常呈現出行波效應,即 VIW。Vandiver[1]和 Moe等[2]將無限長結構模型應用到尾流振子等模型中;Facchinetti[3]等直接采用行波振動解的形式,利用唯象模型研究了結構動力和流體動力以及二者的相互作用。那么,對于海洋工程設計人員來說,在什么條件下可以采用駐波假設的預測模型,在什么條件下又需要采用行波假設的預測模型?是不是只由立管長徑比這個參數來判定立管渦激振動響應形式呢?

筆者利用有限元模型研究了深水細長柔性立管在正弦形式渦激升力作用下的動響應,并通過量綱分析結合函數擬合的方式給出了判定立管渦激振動響應形式的無量綱參數,該參數與系統的阻尼(包括流體阻尼和結構阻尼)、鎖頻模態的階數以及結構長徑比等相關;最后通過實例數值計算給出了該參數的具體表達式和臨界值,并對該參數的物理意義進行了討論。

1 計算模型與振動響應的描述

計算模型如圖1所示,渦激振動時立管的基本平衡方程[4]為

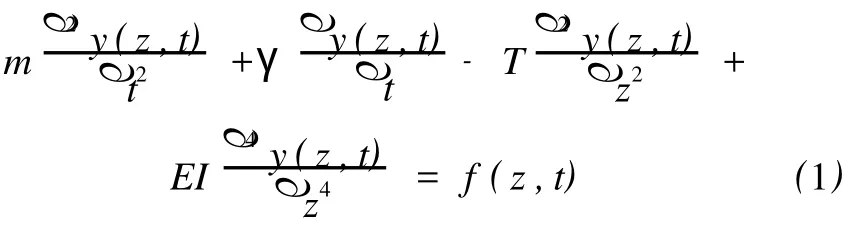
式(1)中:m為單位長度立管質量;γ為結構阻尼;T為立管軸向張力;f(z,t)為垂直流向的流體作用力,包括渦激升力 fv(z,t)和流體阻力 ff(z,t)兩部分。在渦激振動中,流體與固體的相互作用很復雜,目前為止還不能給出精確解。若立管處于鎖頻狀態,一般認為渦激升力和結構運動均為正弦振蕩形式,考慮到計算方便,本文的流體動力部分用系數法給出,即

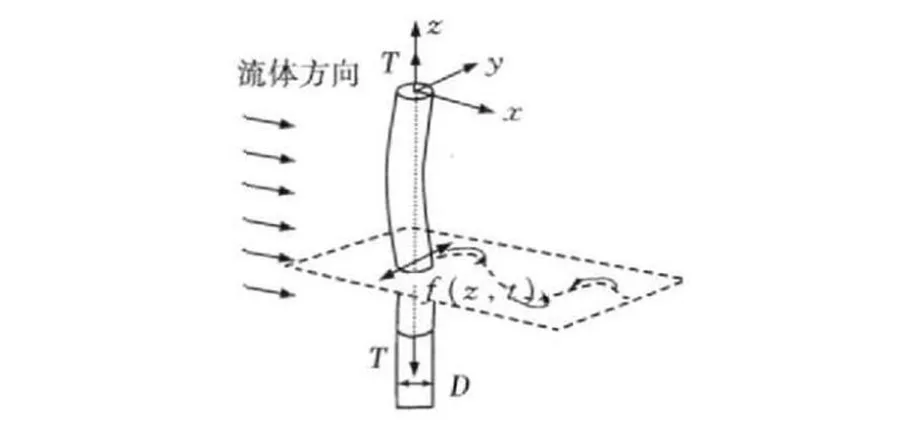
圖1 柔性立管計算模型示意圖[3]

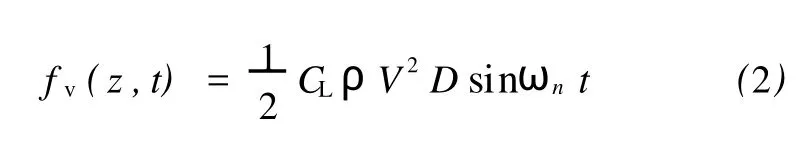
式(2)中:CL為渦激升力系數;ωn為結構的第n階自然頻率。

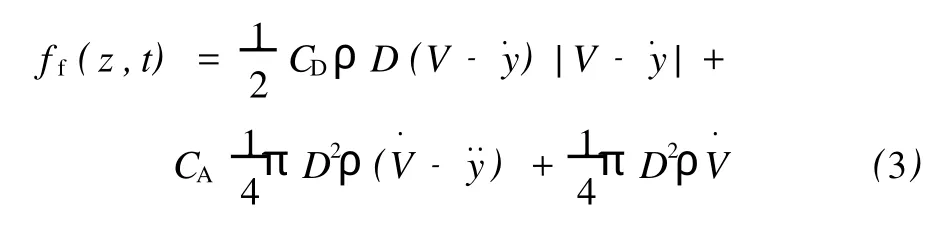
式(3)中水動力系數 CL、CD、CA可以根據經驗或實驗結果確定。

實際平臺立管的約束形式多為底部連接于海底井口的萬向節,頂部連在平臺浮體上。盡管立管頂部會隨平臺在海流作用下做長周期的慢漂運動,但由于其周期很長,相對立管的短周期振動可以不予考慮,所以可以用簡支梁模擬立管結構。簡支梁中任一段柔性立管示意于圖1,為具有代表性,本文將激勵力加載在簡支梁模型中間一點。立管結構的材料和幾何參數為:彈性模量 E為2.1×1011Pa;泊松比為0.3;外徑D、內徑 d分別為1.0、0.89m,長度L分別為250、500、1 000、2 000和3 000m;系統阻尼根據要求變化,起始值取阻尼比ζ為0.25;立管軸向張力 T為6.24×106N。

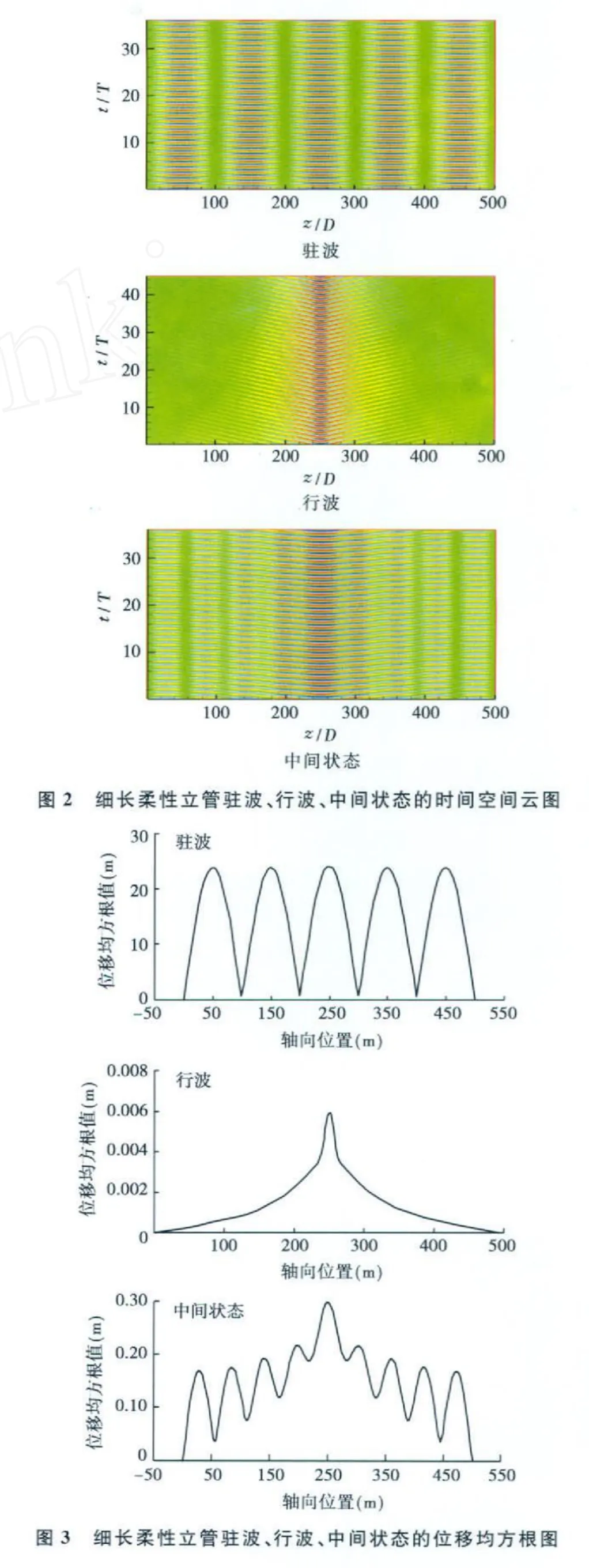
觀察立管響應計算結果,立管響應存在3種振動形式:駐波、行波、中間狀態。3種振動形式對應的時間空間云圖見圖2,3種響應的位移 Green函數均方根見圖3。

由圖3可以看出,駐波、行波是兩種理想的極端狀態。駐波響應存在節點,節點位移一直為零,駐波狀態表明結構發生了共振,沿結構長度方向的各個點上的相位是相同的;行波狀態則表現出無限長結構的特征,即振動波從激振點沿結構向兩端傳播,振幅逐漸衰減直至為零,沒有在端點反射;而中間狀態兼具了以上二者的特征,振動幅值衰減但又表現出一定的周期性。

需要指出的是,筆者在計算時發現,模型參數改變時理想的駐波狀態并不多見,而且它與中間狀態之間是逐漸過渡的,沒有明顯的分界線。目前已有的渦激振動計算軟件(例如SHEAR7、VIVNA等)均是針對駐波振動情況的,不能處理行波振動情況,當響應為中間狀態時,計算軟件給出的結果偏于保守。為了將行波振動區分出來,重點研究了響應何時達到行波。筆者提出用振幅衰減比來判斷響應的類型,即根據沿立管長度方向上同相位點振幅的衰減程度att)來判斷振動是否為行波,其判斷準則為

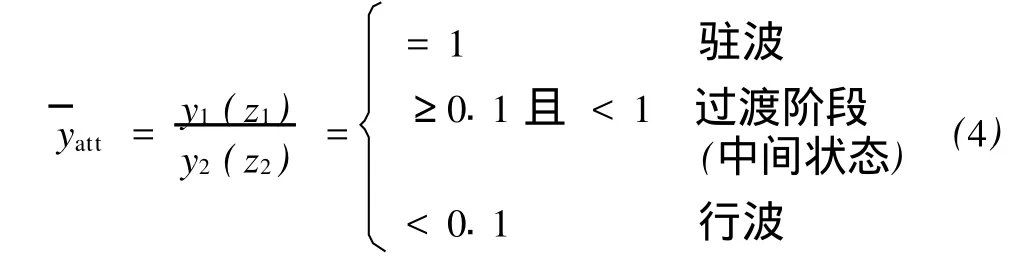
2 判定參數表達式及臨界值的確定

2.1 量綱分析

影響立管結構振動響應形式的因素可分為4類:

(1)幾何因素,包括長度L、外徑D、內徑 d;

(2)材料因素,包括彈性模量 E、結構密度ρm,材料阻尼系數ζs以及泊松比;

(3)結構約束,包括軸向張力 T;

(4)流體因素,包括流體速度V、流體密度ρ、粘性ζf。

根據方程(1)、(3),流體粘性阻尼和振動方向的流體阻尼效果都可以等效到與運動速度成正比的結構粘性阻尼中,即在有限元計算中總阻尼只取粘性阻尼,我們用粘性阻尼比ζ來表征阻尼的大小。

對于實際海洋工程問題,流體為海水,其流體密度ρ、粘性ζf及海流速度已知,立管材料通常選用鋼材或聚酯纖維復合材料,即材料參數和管材的厚度可確定,因此計算模型中結構的內外徑以及軸向張力也取常數。再利用量綱分析方法,將已確定因素的影響用函數Π表示,進行變量量綱處理后可得獨立的無量綱影響因素,包括長徑比 L/D、阻尼比ζ和模態階數n,所以有以下關系式

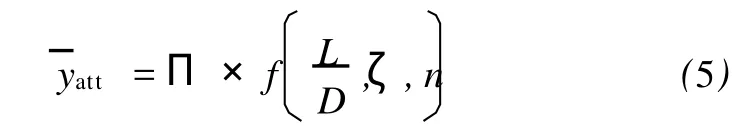
在本文中,主要考慮結構響應由中間狀態轉變為行波時的情況,所以式(5)可以寫成如下形式

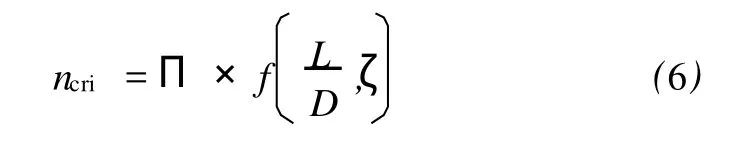
式(6)中:ncri是指結構響應由中間狀態變為行波時的模態階數。

下面通過實例數值計算結合函數擬合的方法,分別給出長徑比L/D、阻尼比ζ與模態階數ncri的關系。

取阻尼比ζ為 0.25,軸向張力 T為 6.24× 106N,立管外徑D為1m,長度L分別為250、500、1 000、2 000、3 000m,即長徑比L/D分別為 250、500、1 000、2 000、3 000。圖4給出了ncri和L/D的關系曲線。其擬合函數為

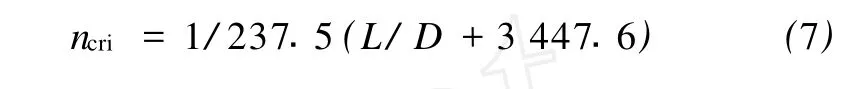
式(7)表明,在此阻尼系數下,即使長度不斷的減小,ncri也不會減小到零,而是趨于一個大于零的數,這個數與阻尼系數有關。

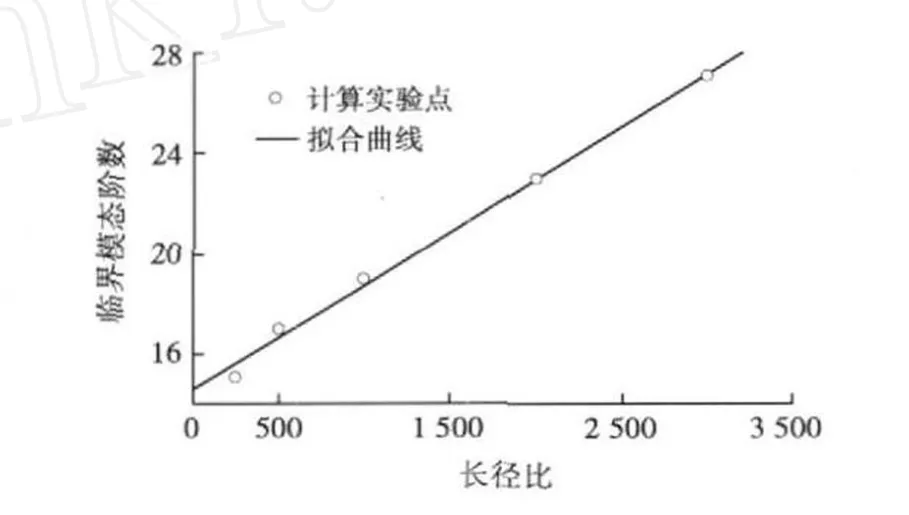
圖4 臨界模態階數與長徑比關系擬合曲線

取軸向張力 T為6.24×106N,立管長度L為500m。數值計算給出的ncri與阻尼比ζ的關系如圖5所示,其擬合函數為ncri=5.2ζ-0.77(8)

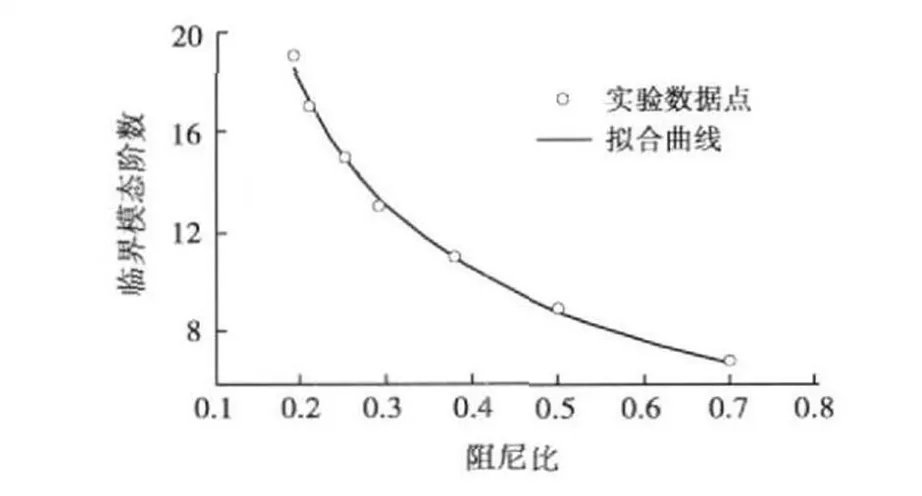
圖5 臨界模態階數與阻尼比關系擬合曲線

2.2 判定參數表達式及臨界值的確定

綜合式(7)和(8),假設 ncri的函數形式為

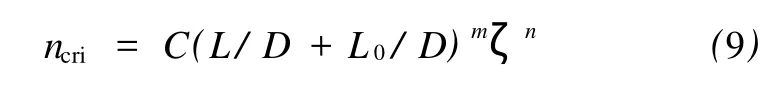
由式(7)可以得到 L0/D=344 7.6,m=1,取 n= -0.77,可以計算得到 C值。由于條件多于未知數,可以得到2個 C值,分別為 C=1/663和 C= 1/690,從工程應用安全考慮,本文取保守值,即 C= 1/663=1.51×10-3。

至此,可以得到 ncri的函數形式

將式(10)改寫成如下形式

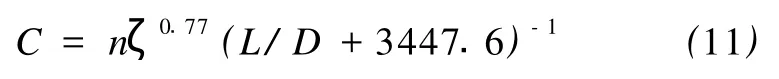
得到了一個無量綱參數 C,其意義表征了立管運動響應振動波的類型,可以作為立管渦激振動響應形式的判定參數。C的臨界值C0=1.51×10-3,可作為中間狀態與行波響應狀態的分界標準,即:若模型C值大于臨界值,則振動響應為行波;若C值小于臨界值,則振動響應為中間狀態或駐波。

為驗證公式(11),我們設計了2個模型。第一個模型的參數為L=1 000m、n=13、ζ=0.45,計算得到此模型的振動響應形式判定參數C=1.58×10-3,大于臨界值C0=1.51×10-3,其響應時空云圖如圖6a所示,可見為明顯的行波響應。第二個模型的參數為L=1 000m、n=11、ζ=0.2,計算得到此模型的振動響應形式判定參數 C=0.72×10-3,小于臨界值 C0=1.51×10-3,其響應時空云圖如圖6b所示,可見還存在一定的周期性,振動響應形式屬于中間狀態。這說明,應用公式(11)給出的無量綱參數 C來判定立管渦激振動的響應形式是可行的。

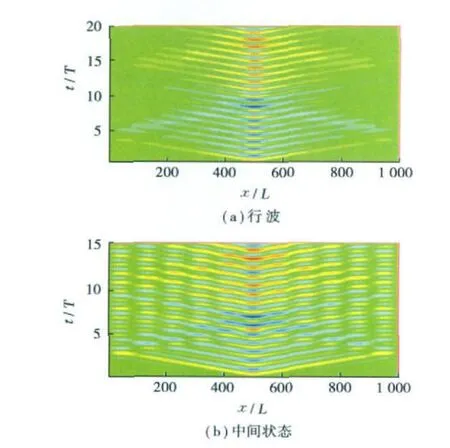
圖6 驗證模型振動響應形式時空云圖

3 判定參數影響因素的討論

由公式(11)可見,判定參數 C中包含模態階數n、長徑比L/D及結構阻尼比ζ等影響因素,而且 n和ζ越大或L/D越小結構響應越容易出行波效應。下面分別討論立管阻尼比ζ、模態階數 n、長度L對判定參數C的影響的物理意義。

(1)阻尼比的影響。如果阻尼比ζ很大(趨于無窮大),則式(11)中的 C值很大(趨于無窮大),此時振動很容易表現為行波效應,即阻尼比越大振動越容易表現為行波,這是由于阻尼比越大,系統的阻尼也越大,結構振動會在沿立管長度方向傳播過程中很快地被阻尼掉,此時振動波尚未到達立管端部而未形成反射波,因此結構響應表現為行波;反之,如果結構阻尼很小甚至趨于零,則式(11)中的 C值很小(趨于零),結構響應更容易表現為駐波效應,這是由于系統的阻尼很小,振動在傳播過程衰減很小,可以傳播到約束端反射回來與正向振動波相互疊加,從而使結構呈現駐波共振。

(2)模態階數的影響。對于一個確定的結構,如果模態階數 n越大,則式(11)中的 C值越大,振動很容易表現為行波效應,即模態階數越高振動越容易表現為行波。這是由于模態階數 n越大,則模態頻率越高,隨之模態阻尼也越大,振動幅值衰減也越快,越容易使響應呈現行波形效應;反之,如果模態階數n越小,模態阻尼也越小,振動很容易表現為駐波效應。

(3)長度的影響。由公式(11)可以看出,立管長度L越大越不容易出現行波效應。對于張力梁,其模態頻率

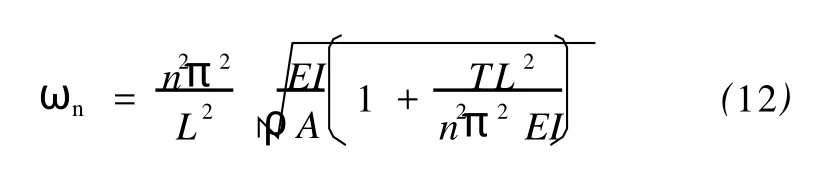
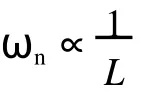
對于圖1所示的模型,波傳播的衰減可表達為e-ζωt。假設結構長度為 L0,在加載點的振幅為 Y0,振動從加載點傳播到距離加載點半個結構長度z點時的振幅為

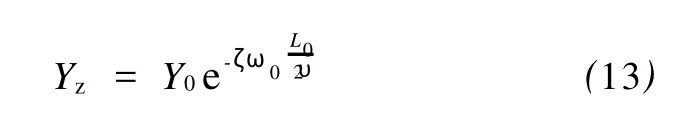
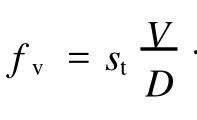
4 結論

利用有限元數值模擬方法研究了深水細長柔性立管在正弦形式渦激升力作用下的動響應,并通過量綱分析結合函數擬合方式給出了判定立管渦激振動響應形式的無量綱參數的表達式和臨界值,該參數與結構長徑比、模態階數及系統阻尼等相關。在實際海洋工程中,當設計或監測人員在預測立管結構的渦激振動響應時,可以先利用本文方法判斷立管結構渦激振動的響應形式,然后根據響應形式再選擇合適的預報模型。

[1] VANDIVER J K.Dimensionless parameters important to the prediction of vortex-induced vibration of long,flexible cylinders in ocean currents[J].Journal of Fluids and Structures.1993, 7(5):423-455.

[2] MOE G,ARNTSEN O.VIV analysis of risers by complex modes[C].11thInternational Offshore and Polar Engineering Conference,2001,3:426-430.

[3] FACCHINETTI.Vortex-induced traveling waves along a cable [J].European J.of Mech.B/Fluids,2004:199-208.

[4] 郭海燕,傅強,婁敏.海洋輸液立管渦激振動響應及其疲勞壽命研究[J].工程力學,2005,22(4):220-224.

(編輯:葉秋敏)

Abstract:The dynamic response of long flexible riser undergoing vortex-induced vibration is studied by using finite element numerical simulation, and provide the expression and critical value of dimensionless parameters for determining response types of long flexible riser undergoing vortex-induced vibration in deepwater.The parameter is correlated with system damp (including liquid damp and structure damp),structure modal order number and structure length.In practice of offshore engineering,the designer could confirm vortex-induced vibration response through selecting an appropriate prediction model based on the response types determined by above method.

Key words:deepwater;riser;vortex-induced vibration;response types;determination parameter

Study on the parameters for determining response types of long flexible riser undergoing vortex-induced vibration in deepw ater

Zhang Liwu Chen Weimin
(Key L aboratory ofEnvironmental Mechanics, Institute of Mechanics,Chinese Academy of Sciences, Beijing,100190)

2009-04-27 改回日期:2009-08-14

＊國家863項目(2006AA09A103-4)、國家自然科學基金項目(10772183,10532070)、中科院方向性項目(KJCX2-YW-L07)部分研究成果。

張立武,男,主要從事深海柔性立管渦激振動響應研究。地址:北京市海淀區北四環西路15號中國科學院力學研究所環境力學重點實驗室(郵編:100190)。E-mail:zhangliwu04@126.com。