如何用SAS軟件正確分析生物醫學科研資料 X. 用SAS軟件實現嵌套設計和裂區設計定量資料的統計分析

陶麗新，胡良平

如何用SAS軟件正確分析生物醫學科研資料 X. 用SAS軟件實現嵌套設計和裂區設計定量資料的統計分析

陶麗新，胡良平

編者按

生物統計學是生物學領域科學研究和實際工作中必不可少的工具，在分子生物學迅速發展的今天，生物統計學更顯示出了它的重要性。實驗設計與數據統計分析是現代生物學的基石，是生物學研究者檢驗假說、尋找模式、建立生物學理論的有利工具，也是生物學研究者探索微觀和宏觀生物世界的必備基礎知識。對于每天甚至是每時每刻涌現的大量的、以天文數字計量的分子遺傳數據，必須借助統計學知識加以分析處理，才能從中獲得有意義的信息。“生物多樣性數據分析”是開展生物多樣性研究的一個重要方面，數據分析能力的高低極大地影響著我們對各種生態學現象認識的深度和廣度。現在，電子計算機的普及使得生物統計分析過程大大簡化，生物統計分析軟件包的普及將生物統計學從統計學家的書本里解放了出來，簡化了生物統計分析過程，使之成為生物學研究者的常用工具。本刊特邀軍事醫學科學院生物醫學統計學咨詢中心主任胡良平教授，以“如何用 SAS 軟件正確分析生物醫學科研資料”為題，撰寫系列統計學講座，希望該系列講座能對生物醫學科研工作者有所幫助。

1 嵌套設計及其資料的統計分析

1.1 嵌套設計的概念及應用場合

試驗中涉及兩個或多個試驗因素，且依據專業知識可以認為各試驗因素對觀測指標的影響有主次之分，主要因素各水平下嵌套著次要因素，次要因素各水平下又嵌套著更次要的因素，這樣的試驗設計稱為嵌套設計。此類設計有兩種情形：第一種情形是，受試對象本身具有分組再分組的各種分組因素，處理（即最終的試驗條件）是各因素各水平的全面組合，且因素之間在專業上有主次之分（如年齡與性別對心室射血時間的影響，性別的影響大于年齡）；第二種情形是，受試對象本身并非具有分組再分組的各種分組因素，處理（即最終的試驗條件）不是各因素各水平的全面組合，而是各因素按其隸屬關系系統分組，且因素之間在專業上有主次之分（如研究不同代次不同家庭成年男性的身高資料，不同家庭之間的差別大于同一個家庭內部不同代次之間的差別）。

嵌套設計主要應用于試驗因素對觀測指標的影響有主次之分的試驗研究中，試驗因素之間的主次關系要有專業依據，不能憑空想象而定[1-2]。嵌套設計的構造方法和列表格式參見例 1。

1.2 嵌套設計定量資料方差分析的 SAS 實現

例 1在4塊相同的試驗田中考察肥力和小麥品種對小麥產量的影響，并且假定品種和肥力對產量的影響大小順序為品種 > 肥力，資料如表1所示。試分析小麥品種和肥力對小麥產量的影響有無統計學意義。

分析與 SAS 實現：該資料涉及兩個試驗因素，分別為品種與肥力，各有3個水平，兩因素各水平全面組合，各種組合條件下進行了 4 次獨立重復試驗；又由于品種與肥力對產量的影響大小順序為品種 > 肥力，所以該資料為系統分組（或嵌套）設計。

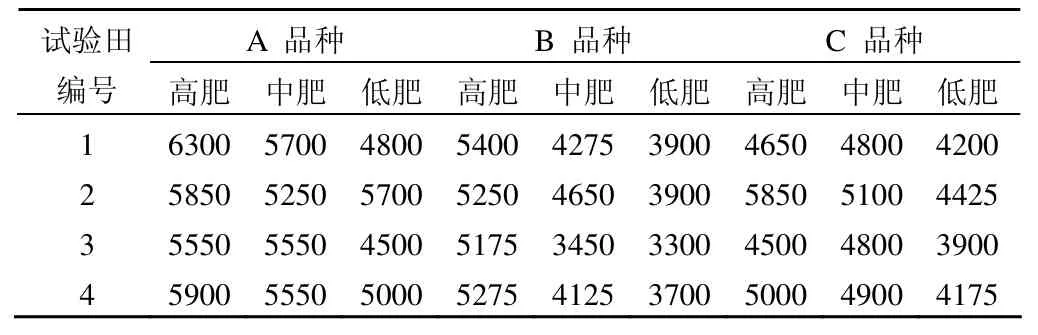
表1 不同小麥品種和肥力對小麥產量（kg/ha）的影響

具體的 SAS 程序如下：

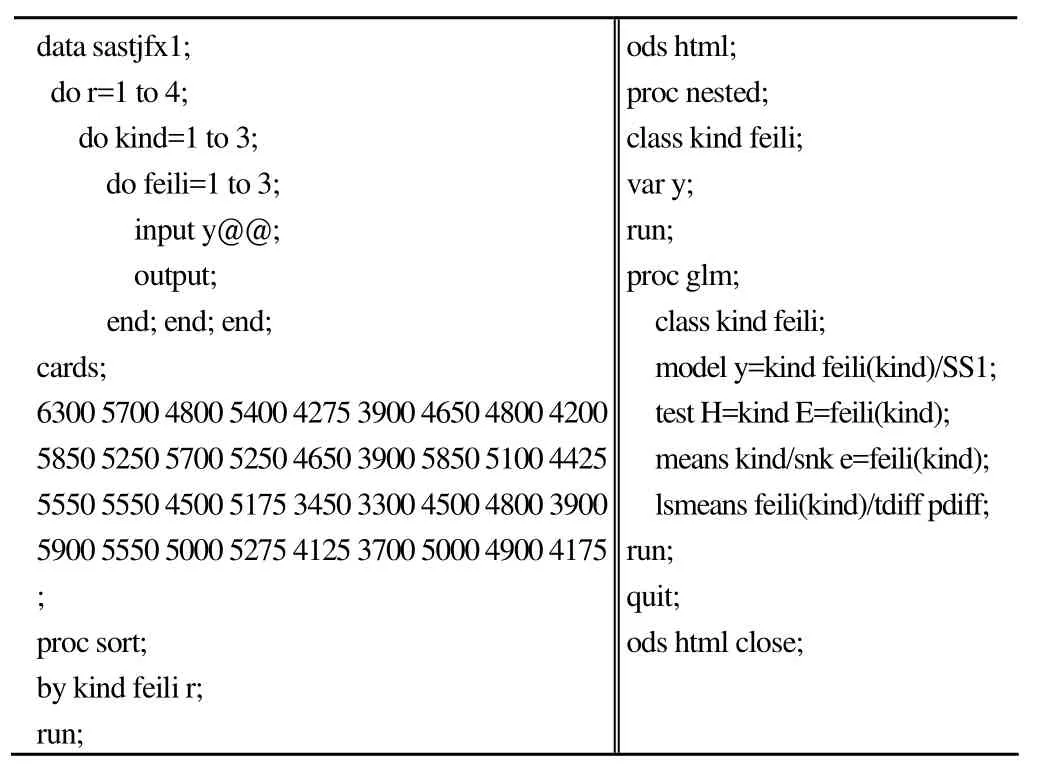
data sastjfx1;do r=1 to 4;do kind=1 to 3;do feili=1 to 3;input y@@;output;end; end; end;cards;6300 5700 4800 5400 4275 3900 4650 4800 4200 5850 5250 5700 5250 4650 3900 5850 5100 4425 5550 5550 4500 5175 3450 3300 4500 4800 3900 5900 5550 5000 5275 4125 3700 5000 4900 4175;proc sort;by kind feili r;run;ods html;proc nested;class kind feili;var y;run;proc glm;class kind feili;model y=kind feili(kind)/SS1;test H=kind E=feili(kind);means kind/snk e=feili(kind);lsmeans feili(kind)/tdiff pdiff;run;quit;ods html close;

作者單位：100850 北京，軍事醫學科學院生物醫學統計學咨詢中心

程序說明：數據步建立數據集 sastjfx1，輸入變量名和變量值，“r”、“kind”、“feili”、“y”分別代表試驗田編號、小麥品種、肥力和小麥產量。sort 過程是對數據集中的變量按照主次重新排序；nested 過程用于對變量已經按照主次排序且來自嵌套設計的平衡資料的方差分析；第 3 個過程為glm 過程，glm 過程的適用面很寬，資料可以是不平衡的，也可以不排序，僅取決于 model 語句和 test 語句的寫法，“model y = kind feili (kind)/SS1”表示因素肥力嵌套在品種里，“SS1”表示第 I 型離均差平方和（計算結果與變量在model 語句中的順序有關），不能選用 SS3；“H = kind E =feili (kind)”表示在考察品種的效應時，以模型中肥力的效應作為誤差項。程序中同時使用了 nested 過程和 glm 過程對資料進行分析。

SAS 輸出結果與結果解釋：

The NESTED procedure

上述結果表明：F = 2.71，P = 0.1453；F = 11.06，P <0.0001，說明就該資料而言，肥力對小麥產量的影響具有統計學意義，但是還沒有理由說明小麥品種對小麥產量的影響具有統計學意義。

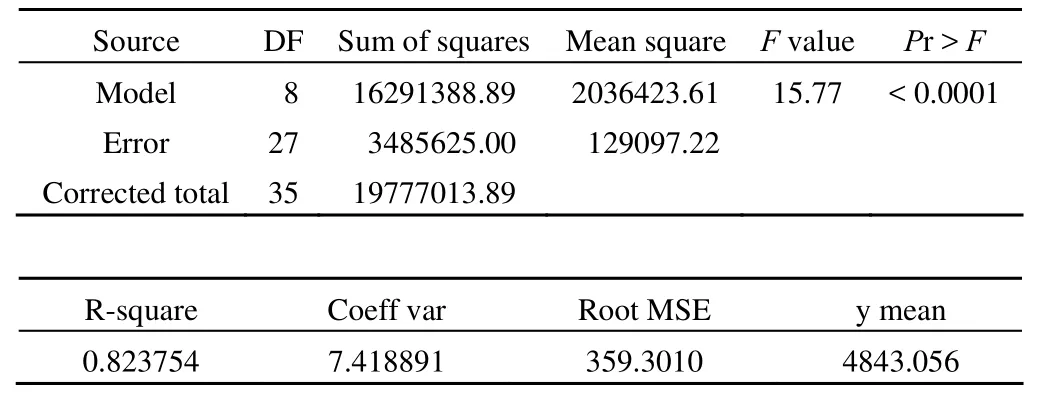
The GLM procedure dependent variable: y

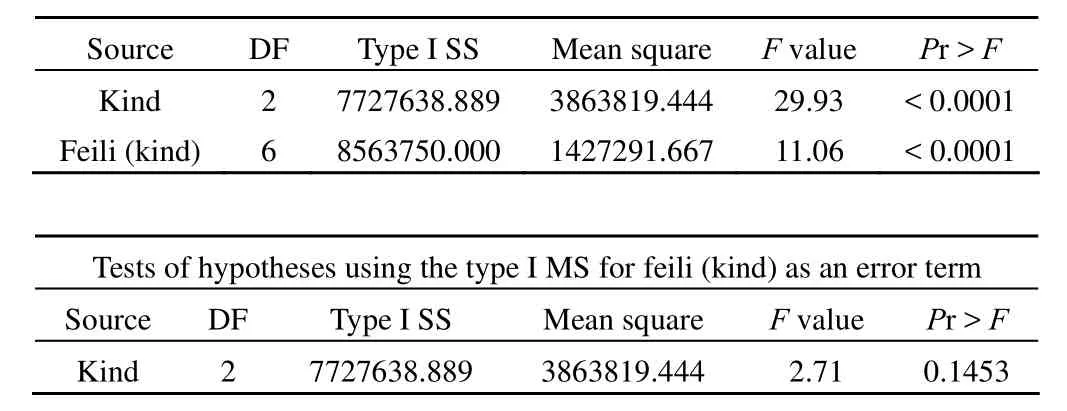
Source DF Type I SS Mean square F value Pr > F Kind 2 7727638.889 3863819.444 29.93 < 0.0001 Feili (kind) 6 8563750.000 1427291.667 11.06 < 0.0001 Tests of hypotheses using the type I MS for feili (kind) as an error term Source DF Type I SS Mean square F value Pr > F Kind 2 7727638.889 3863819.444 2.71 0.1453

上述結果表明：F = 15.77，P < 0.0001，說明總模型具有統計學意義；模型的分項部分只有對肥力分析的結果是正確的，其 F = 11.06，P < 0.0001，說明肥力對小麥產量的影響具有統計學意義；由 test 語句給出的結果，才是對主要因素（小麥品種）的合理檢驗，其 F = 2.71，P = 0.1453，說明小麥品種對小麥產量的影響沒有統計學意義。

Least squares means for effect feili (kind)t for H0: LSMean (i) = LSMean (j) / Pr > |t|Dependent variable: y

以上是 9 種組合情況的小麥產量均值之間兩兩比較的結果，小麥品種為 A 時，由 t = –3.54241，P = 0.0015 說明高肥與低肥比較小麥產量之間的差別有統計學意義；由t = –1.52521，P = 0.1388 說明高肥與中肥比較小麥產量之間的差別沒有統計學意義；由 t = –2.01721，P = 0.0537 說明中肥與低肥比較小麥產量之間的差別沒有統計學意義。小麥品種為 B 時，由 t = –4.52642，P = 0.0001 說明高肥與中肥比較小麥產量之間的差別有統計學意義；由 t = –6.19922，P < 0.0001 說明高肥與低肥比較小麥產量之間的差別有統計學意義；由 t = –1.67281，P = 0.1059 說明中肥與低肥比較小麥產量之間的差別沒有統計學意義。小麥品種為 C時，由 t = –0.3936，P = 0.6970 說明高肥與中肥比較小麥產量之間的差別沒有統計學意義；由 t = –3.24721，P = 0.0031說明高肥與低肥比較小麥產量之間的差別有統計學意義；由t = –2.85361，P = 0.0082 說明中肥與低肥比較小麥產量之間的差別有統計學意義。

The GLM procedure

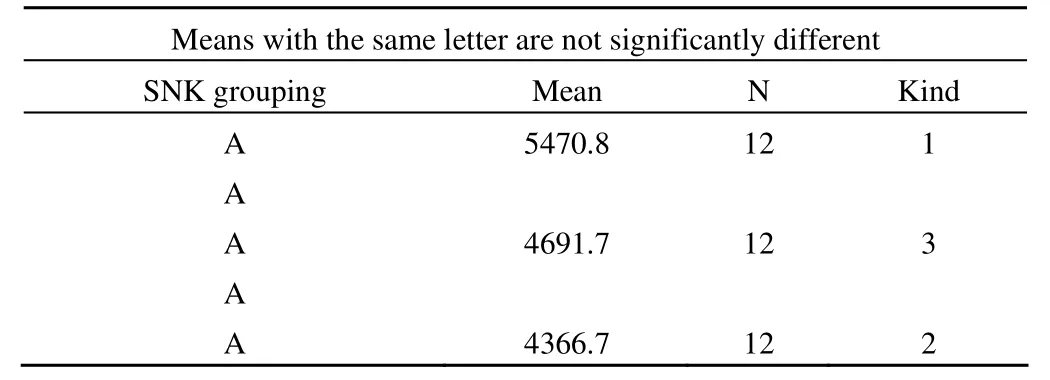
Student-newman-keuls test for y

上述結果表明：不同小麥品種之間小麥產量的差別沒有統計學意義。而小麥品種為 A時，高肥的小麥產量高于低肥的小麥產量；小麥品種為 B 時，高肥的小麥產量高于中肥和低肥的小麥產量；小麥品種為 C 時，高肥的小麥產量高于低肥的小麥產量，中肥的小麥產量高于低肥的小麥產量。

2 裂區設計及其資料的統計分析

2.1 裂區設計的概念及應用場合

試驗因素分階段進入試驗過程，通常由先進入試驗的試驗因素（設為 A）構成單因素多水平設計或由先進入試驗的試驗因素（設為 A）與區組因素（設為 B）構造出含 m次獨立重復試驗的隨機區組設計；再把接受因素 A 各水平處理或接受因素 A 與因素 B 各組合水平處理的 m 個受試對象隨機地分配給在第二階段進入試驗的試驗因素 C的 m 個水平，這樣安排試驗因素的方法稱為裂區設計或分割設計。

結合實際問題，當試驗研究過程自然形成 2 個或多階段（有時稱為工序），各階段涉及的試驗因素彼此不同，但需要等整個試驗過程結束后，才能觀測定量指標的結果，就需要用到此設計[1-2]。裂區設計的構造方法和列表格式參見例 2。

2.2 裂區設計定量資料方差分析的 SAS 實現

例 2在 3 塊不同的試驗田中進行玉米的施肥試驗。在苗期對每塊試驗田使用不同的施氮量，即正常施用苗肥（78 kg/hm2）和減少 1/3 苗肥（52.5 kg/hm2）；在 5 葉期，采用灌根法每公頃用清水 600 kg，分別加入不同用量的農夫樂，充分攪拌后，分株劑量澆灌在玉米根部。資料如表2所示。試分析不同的施氮量和不同的農夫樂用量對玉米產量的影響。

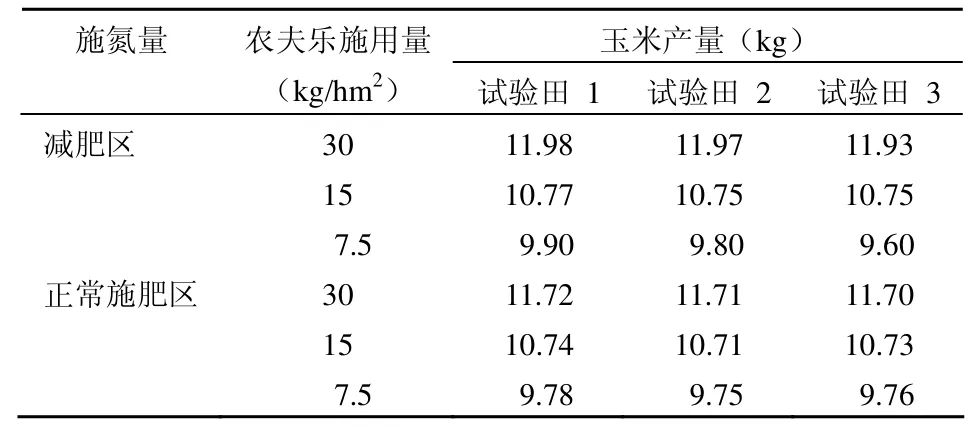
表2 不同施氮量和不同農夫樂施用量對玉米產量的影響

分析與 SAS 實現：該資料中，試驗因素“不同施氮量”和區組因素在苗期先出現在試驗中，每個區組被分成兩個一級單位；當玉米生長到 5 葉期時，每個一級單位再被分為3 個二級單位，分別施加 3 種不同用量的農夫樂，定量的觀測指標為玉米產量，兩個試驗因素分兩個階段進入試驗過程，所以該資料為裂區（或分割）設計。

具體的 SAS 程序如下：

data sastjfx2;do a=1 to 2;do b=1 to 3;do s=1 to 3;input x @@;output;end;end;end;cards;11.98 11.97 11.93 10.77 10.75 10.75 9.90 9.80 9.60 11.72 11.71 11.70 10.74 10.71 10.73 9.78 9.75 9.76;ods html;proc glm;class a s b;model x=a s a*s b a*b/ss3;test h=a s e=a*s;means a*b;lsmeans a*b/tdiff pdiff;run;quit;ods html close;

程序說明：數據步建立數據集 sastjfx2，輸入變量名和變量值，“a”、“b”、“s”、“x”分別代表不同施氮量、農夫樂的不同施用量、試驗田編號和玉米產量。過程步調用 glm過程，“test h = a s e = a*s;”表示在分析因素 a 和區組因素s 時，以它們的交互作用的均方作為誤差的均方（注意：若出現各組例數不等或某些試驗條件下未做試驗，應使用 glm過程來實現計算）。

SAS 輸出結果與結果解釋：

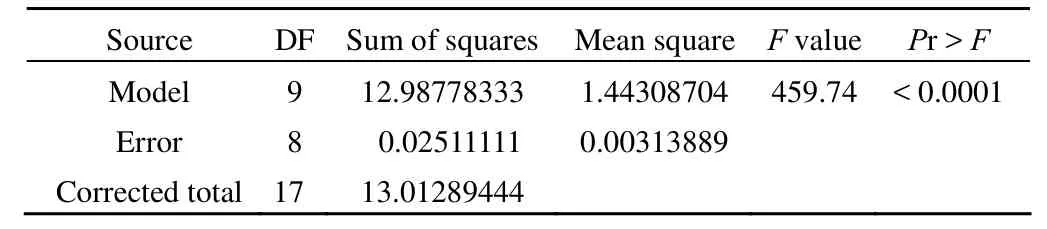
The GLM procedure dependent variable: x

以上結果表明：F = 459.74，P < 0.0001，說明總的模型具有統計學意義。

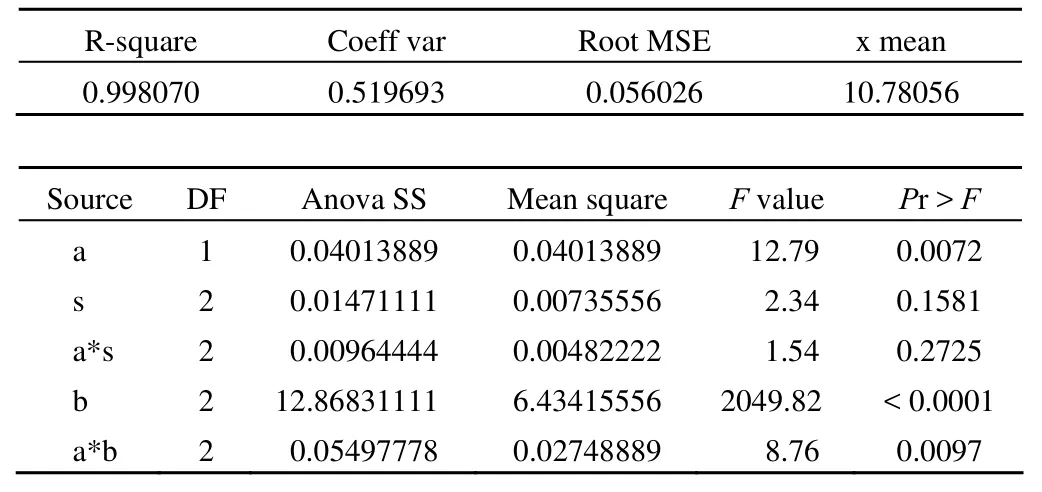
R-square Coeff var Root MSE x mean 0.998070 0.519693 0.056026 10.78056 Source DF Anova SS Mean square F value Pr > F a 1 0.04013889 0.04013889 12.79 0.0072 s 2 0.01471111 0.00735556 2.34 0.1581 a*s 2 0.00964444 0.00482222 1.54 0.2725 b 2 12.86831111 6.43415556 2049.82 < 0.0001 a*b 2 0.05497778 0.02748889 8.76 0.0097

以上結果表明：對 a * s 的檢驗，F = 1.54，P = 0.2725，說明不同施氮量與隨機區組 s 之間的交互作用沒有統計學意義；對 b 的檢驗，F = 2049.82，P < 0.0001，說明農夫樂不同施用量對玉米產量的影響具有統計學意義；對 a * b 的檢驗，F = 8.76，P = 0.0097，說明不同的施氮量和農夫樂的不同施用量之間的交互作用具有統計學意義。

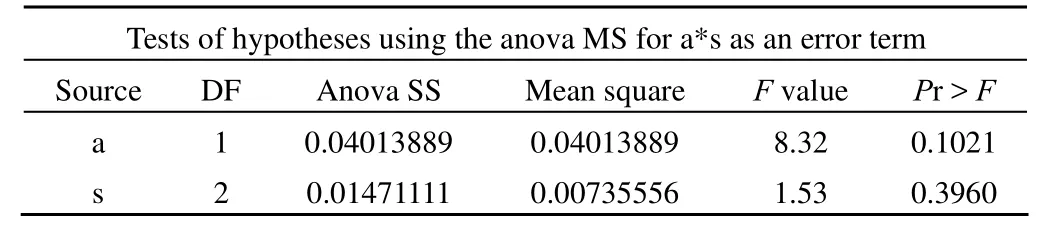
Tests of hypotheses using the anova MS for a*s as an error term Source DF Anova SS Mean square F value Pr > F a 1 0.04013889 0.04013889 8.32 0.1021 s 2 0.01471111 0.00735556 1.53 0.3960

以上結果表明：F = 8.32，P = 0.1021；F = 1.53，P =0.3960，說明不同的施氮量和不同的試驗田對玉米產量的影響之間的差別沒有統計學意義。

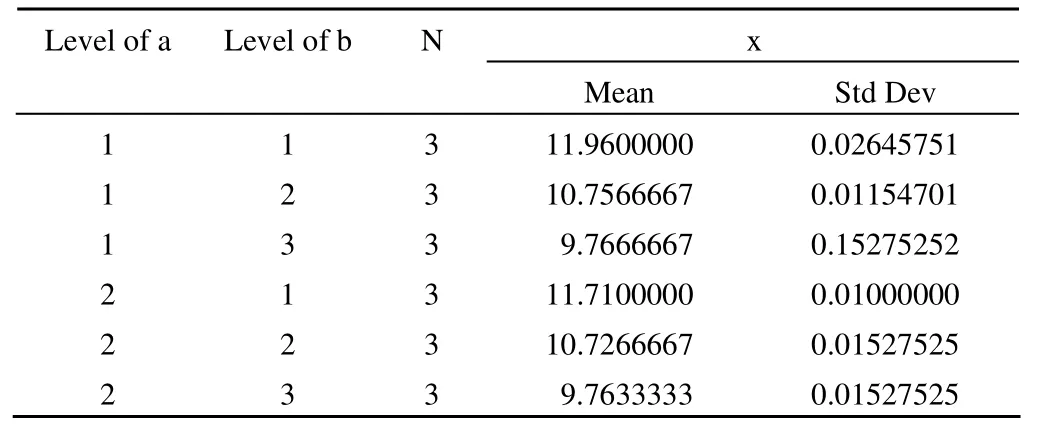
Level of a Level of b N x Mean Std Dev 1 1 3 11.9600000 0.02645751 1 2 3 10.7566667 0.01154701 1 3 3 9.7666667 0.15275252 2 1 3 11.7100000 0.01000000 2 2 3 10.7266667 0.01527525 2 3 3 9.7633333 0.01527525

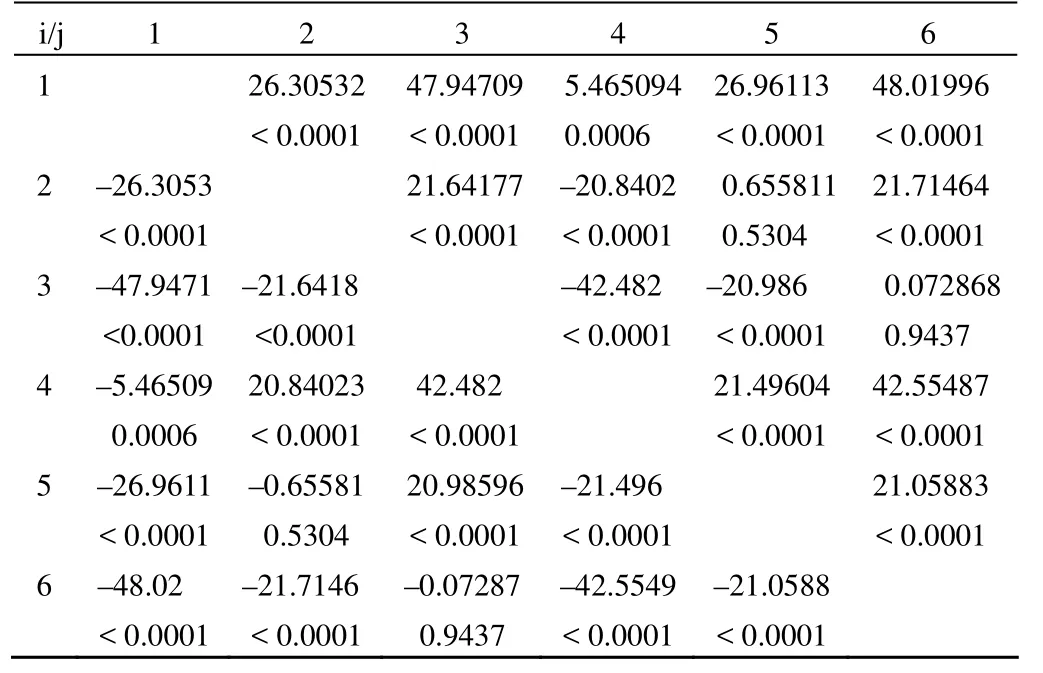
Least squares means for effect a*b t for H0: LSmean (i) = LSmean (j) / Pr > |t|Dependent variable: x

以上是 6 種組合條件下玉米產量均值之間兩兩比較的結果。對減肥區而言，由 t = –26.3053，P < 0.0001 說明農夫樂施用量為 30 kg/hm2與農夫樂施用量為 15 kg/hm2之間玉米產量的差別有統計學意義；由 t = –47.9471，P <0.0001 說明農夫樂施用量為 30 kg/hm2與農夫樂施用量為7.5 kg/hm2之間玉米產量的差別有統計學意義；由 t =–21.6418，P < 0.0001 說明農夫樂施用量為 15 kg/hm2與農夫樂施用量為 7.5 kg/hm2之間玉米產量的差別有統計學意義。對正常施肥區而言，由 t = –21.496，P < 0.0001 說明農夫樂施用量為 30 kg/hm2與農夫樂施用量為 15 kg/hm2之間玉米產量的差別有統計學意義；由 t = –42.5549，P <0.0001 說明農夫樂施用量為 30 kg/hm2與農夫樂施用量為7.5 kg/hm2之間玉米產量的差別有統計學意義；由 t =–21.0588，P < 0.0001 說明農夫樂施用量為 15 kg/hm2與農夫樂施用量為 7.5 kg/hm2之間玉米產量的差別有統計學意義。

由以上結果可以看出，減肥區和正常施肥區比較玉米產量之間的差別沒有統計學意義；但是無論是減肥區還是正常施肥區，農夫樂施用量的不同造成的玉米產量之間的差別都具有統計學意義，玉米產量的高低順序為農夫樂施用量30 kg/hm2> 15 kg/hm2> 7.5 kg/hm2。

[1] Hu LP. Application of statistical triple-type theory in the experiment design. Beijing: People’s Military Medical Press, 2006: 85-93. (in Chinese)胡良平. 統計學三型理論在實驗設計中的應用. 北京: 人民軍醫出版社, 2006: 85-93.

[2] Hu LP. The practical course in the statistical analysis for windows SAS, version 6.12 & 8.0. Beijing: Press of Military Medical Sciences,2001:215-222. (in Chinese)胡良平. Windows SAS 6.12 & 8.0實用統計分析教程. 北京: 軍事醫學科學出版社, 2001: 215-222.

10.3969/cmba.j.issn.1673-713X.2010.04.017

胡良平，Email：lphu812@sina.com