多基站數據聚合無線傳感器網絡中的最大生命期路由

唐偉，郭偉

(電子科技大學 通信抗干擾技術國家級重點實驗室, 四川 成都 611731）

1 引言

無線傳感器網絡（WSN, wireless sensor networks）通常由一組固定的傳感器節點和一組基站構成[1]。傳感器節點負責收集區域內的信息，并將這些信息封裝為數據報文，通過多跳的方式傳遞至基站。常見的應用包括分布式壓縮[2,3]、目標跟蹤[4,5]以及環境監測[6,7]等。無線傳感器節點往往只配有不可再生的電池，能量極為有限，因此需要設計節能路由算法以最大化網絡生命期。而路由算法設計主要需要考慮以下幾個方面。首先，鄰近節點所收集的數據之間往往具有很強的相關性，通常采用數據聚合來消除數據中的冗余信息[8,9]。其次，網絡中可能存在多個基站，相比單一基站的情形更加復雜，基站間的數據流量的合理分配以及節點數據的路由路徑等都需要在算法設計中解決[10]。

由于數據聚合會改變網絡中的數據流量，因而路由協議的設計上必須要考慮數據流量的變化。現有的數據聚合模型包括分布式壓縮模型[11]、局部Slepian-Wolf編碼模型[12]以及隨機場模型[13]等。例如，文獻[14]對分布式壓縮模型下的節能路由進行了研究，證明了在此情況下網絡總體能耗的最優化問題中，壓縮算法與網絡的路由結構可以分別獨立考慮。由于分布式壓縮模型中需要獲得全網的數據相關信息，難以實現。因此，文獻[12]考慮了局部壓縮算法，即節點只與鄰居進行信息交換與數據壓縮的局部Slepian-Wolf編碼，并通過線性規劃的方法獲得網絡最小能耗路由算法。文獻[15]考慮了馬氏隨機場中的最小總能耗路由，并提出了一種基于最小生成樹的啟發式路由算法。文獻[16]研究了高斯隨機場中的最優路由問題，對比分析了最小跳數路由、最小能耗路由以及Chernoff路由的性能。

現有大部分路由算法以網絡總體能耗為目標函數，難以準確反映網絡的生命期；盡管有人提出了一些最大化網絡中節點最小生命期的路由算法，然而還很少有將節點功率控制、數據聚合以及多基站三者相結合的路由算法。為此，本文首先分析了多基站無線傳感器網絡中最大網絡生命期路由問題的NP-hard性質，然后提出了一種基于生成森林的啟發式算法。為了設計分布式算法，本文采用了次梯度方法。最后，本文通過大量仿真實驗驗證了啟發式算法的性能，并表明所提出的分布式算法能夠有效地收斂。

本文組織如下。第2節介紹系統模型。第3節給出最大生命期問題，并證明其NP-hard性質。第4節提出基于最小生成森林的啟發式路由算法。第5節設計網絡最大化生命期問題的分布式算法。第6節是仿真實驗及結果分析。第7節是結束語。

2 系統模型

考慮一個無線傳感器網絡，其中節點之間通過雙向無線鏈路通信，網絡中的每個節點與至少一個基站連通。網絡可以被抽象為一個無向圖G(V?,E)，其中V?表示網絡中的傳感器節點和基站的集合，E表示鏈路的集合。記網絡中的傳感器節點集合為V，基站集合為S，則記節點i∈V的鄰居集合為傳感器節點初始能量為 Ei（單位是Joule），基站沒有能耗限制。每個傳感器節點i∈V連續或周期性地向基站報告所收集到的數據，且數據產生率為 Ri。其中，只要任意一個基站收集到數據，該數據就算被成功接收。由于無線傳感器網絡具有很強的面向應用性，本文假定網絡鏈路具有足夠帶寬傳輸數據。對于無線信道中的沖突、干擾等，可以通過物理層和鏈路層技術進行抑制，目前已有大量文獻對此進行研究，而本文重點研究該類網絡中的路由問題。

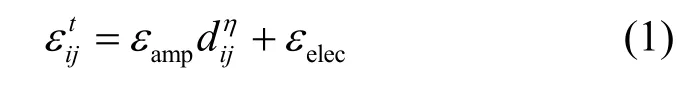
3 最大生命期路由問題

記網絡中通過鏈路(i,j)∈E的網絡流為fij。由于采用了數據聚合，網絡中的數據可以被分為2類：節點自身收集的原始數據以及去除了冗余信息的聚合數據。因此，網絡流可以被表示為

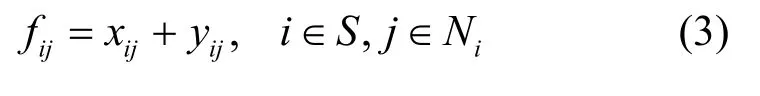
根據式(1)和式(2)，對于網絡中的任意傳感器節點i∈V，其能量消耗速率可以被表示為

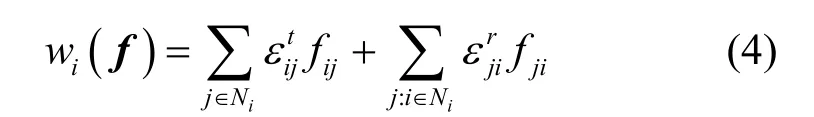
由此，定義節點的歸一化能量消耗率 ωi（f）于是，節點i在對應的網絡流 f下的生命期可以被表示為。定義網絡生命期為第一個因為能量耗盡而死亡的節點的生命期[18]。由于該定義下網絡的生命期往往是其他定義下網絡生命期的下界，例如網絡分裂時的生命期、網絡失去功能時的生命期等等，因此在研究上具有重要意義。通過定義知于是可以得到定義網絡歸一化的能量消耗率為，于是有最大化Tnet（f），等價于最小化

minimize Ω

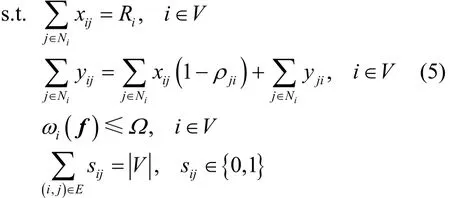
式(5)表示問題的目標是最小化網絡歸一化能量消耗率Ω，即最大化網絡生命期 Tnet。第1項約束表示離開節點 i的原始數據網絡流必須等于節點i自身產生的原始數據率。第2項約束表示離開節點 i的聚合數據網絡流必須等于來自其他節點的原始數據壓縮所得的聚合數據率與來自其他節點的聚合數據網絡流之和。第3項約束表示網絡中各節點的歸一化能量消耗率都不超過網絡的歸一化能量消耗率Ω。第四項約束表示所有網絡流的選擇數量之和為網絡中傳感器節點的數目。第1、第2及第4項約束一起，表明了網絡中的聚合數據網絡流構成一棵沒有環路的生成樹[19]，即節點 i向且只向一個鄰居節點輸出聚合數據網絡流，聚合數據網絡流最終匯集到基站。下面的定理給出了問題的NP-hard性質。

定理 1網絡最大生命期路由問題是一個NP-hard問題。

證明考查經典的集覆蓋問題（set cover problem），該類問題已經被證明為一類NP-hard問題[20]。問題描述如下：對于集合 F及其子集的集合其中，以及一個正整數K，找到元素個數為K集合使得

首先，將集覆蓋問題映射為一個無線傳感器網絡。如圖1所示，網絡中有+ 2個傳感器節點，分別對應于集合 F中的元素為其子集的集合C中的元素為，以及兩個瓶頸節點 b1,b2；同時還有S個基站對于任意的當 ai∈cj時，網絡中對應地存在一條鏈路(ai, cj)；每個 cj與 b1,b2間都存在一條鏈路；且 b1,b2與每個基站間都存在一條鏈路。每個傳感器節點的數據產生率都是 1bit/s，每條鏈路的能量開銷都是 1J/bit，各鏈路的數據相關性指標都是ρ＜0.5。傳感器節點a1,a2,… ,aF的初始能量為1J， cj的初始能量為b1的初始能量為b2的初始能量是，基站的初始能量足夠大。顯然，網絡可以在多項式時間內通過一個集覆蓋問題來構建。

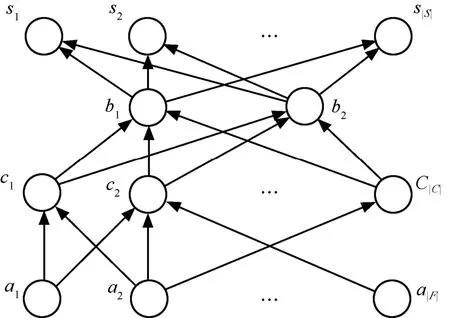
圖1 集覆蓋問題向網絡最大生命期問題的轉化

然后，考慮使得網絡生命期最大的網絡流。對應于集覆蓋問題的一個最優解令其中各元素所對應的節點將其原始數據和聚合數據都傳遞至 b1，而余下的C中元素所對應的節點將其原始數據和聚合數據都傳遞至 b2。于是，瓶頸節點 b1需要傳遞來自和）的聚合數據及其自身的原始數據，故其能量消耗率為；而瓶頸節點b2需要傳遞來自節點的聚合數據及其自身的原始數據，故其能量消耗率為。因而網絡恰好能夠存活1s。同時，這也是網絡的最大生命期。因為瓶頸節點 b1和 b2總共需要傳遞(bit/s)的數據流量，而總能量恰好為生命期不超過1s。由此，求解該類問題的NP-hard性質得證。

根據定理 1，該類網絡中的最大生命期問題是難以直接進行求解的。為此，在下面2節中，本文提出一種啟發式路由算法來獲取問題的近似解。

4 基于最小生成森林的路由算法

為了在多基站無線傳感器網絡中實現最小生成森林，本文采用了偽樹根（pseudo root）方法[21]。如圖2所示，其中圓點表示傳感器節點，五角形表示基站，而中央的多刺形表示偽樹根。偽樹根與各基站通過偽鏈路（pseudo link）相連，且偽鏈路開銷為 0。認為數據全部匯集到偽樹根，而每條實際鏈路上的開銷為鏈路兩端節點傳輸單位比特數據所需的總功率，即

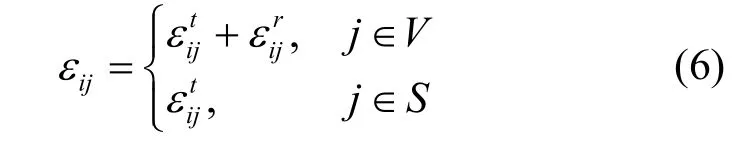
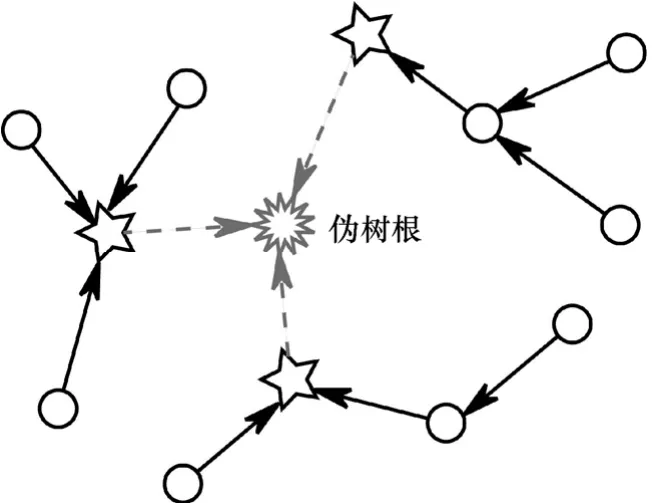
圖2 多基站無線傳感器網絡中的最小生成森林

對網絡中的每個傳感器節點iV∈，記該節點在生成樹中的父節點為pi，節點i的全部聚合數據都轉發給pi。于是，網絡流y與網絡流x存在如下關系

注意式(7)中，對于生成樹中的葉節點（不是任何節點父節點的節點）l，有 y是，通過遞推，網絡流y可以被網絡流x唯一確定，因而節點的能耗也可以用x表示。注意到x與y呈線性關系，即對于每條網絡流 yij都存在一組系數ζ（ij）使得。因而，有

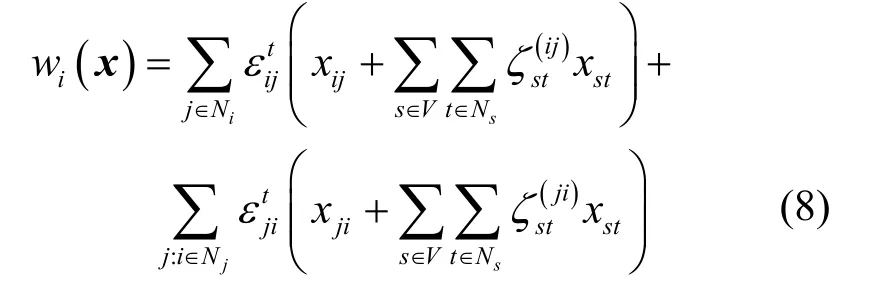
于是，基于生成樹的多基站最大生命期路由問題可以被表示為如下線性規劃問題

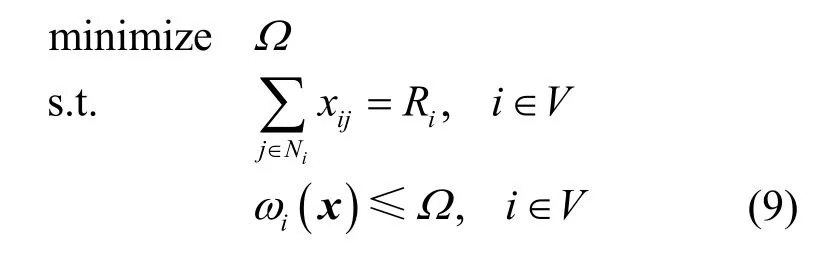
由于無線傳感器網絡是一類分布式網絡，通常要求路由算法具有分布式性質。為此，本文采用投影次梯度方法[22]來解決。

5 網絡最大化生命期問題的分布式算法

5.1 投影次梯度方法

對于n維向量 x ∈ ?n，考慮如下最優化問題minimize subject to

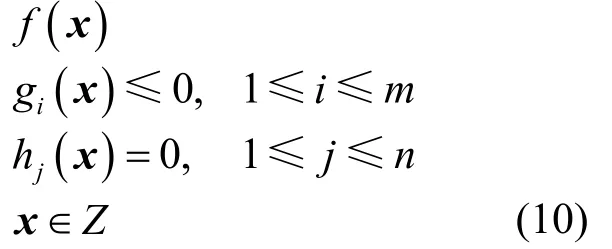
其中，f是嚴格凸函數，ig是凸函數，jh是仿射函數，而Z是n?中的有界凸多面體。目標函數對應的拉格朗日函數為

對于n?+∈λ，定義

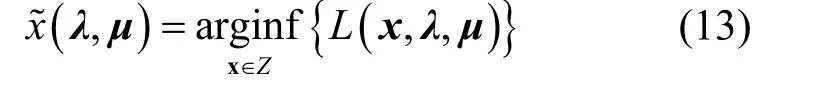
x?（λ, μ ） 是唯一的。 d （λ, μ ）在（λ*, μ*） 處的一組次梯度可以表示為。于

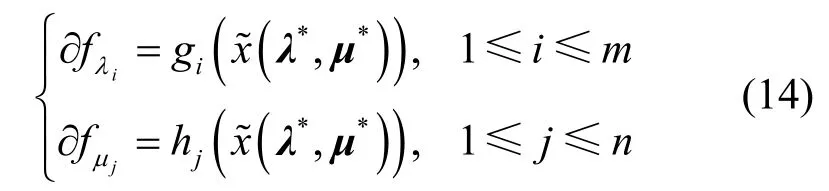
投影次梯度方法是一種迭代方法，且將迭代得到的拉格朗日乘數投影到定義域[23]。設初始的拉格朗日乘數為（λ(1), μ(1)）。在第 k ≥ 1步中，對拉格朗日乘數做如下更新

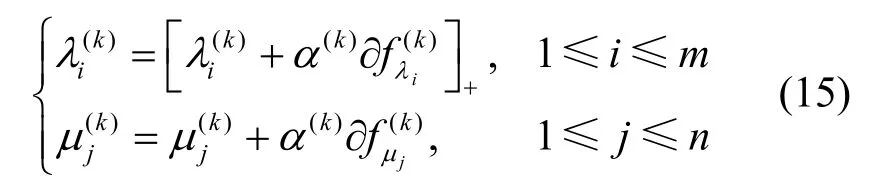
其中，()kα 是迭代步長。滿足下列條件時

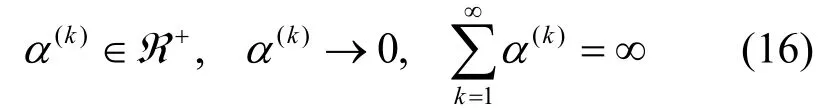
迭代算法收斂于 d （λ, μ ）的最大值。若強對偶性質成立，則序列收斂于原始問題的最優解[24]。

5.2 分布式算法

為了應用次梯度方法，需要將問題(9)中的目標函數轉化為一個嚴格凸函數。為此，可以用目標函數Ω2替換原來的目標函數Ω，并引入二次協調項其中β是一個足夠小的正實數。于是，得到如下最優化問題

minimize subject to

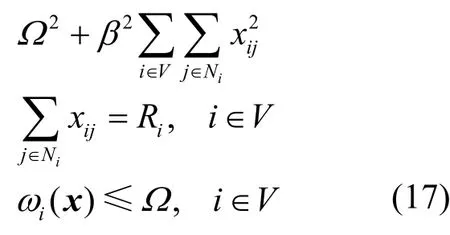
式(17)的拉格朗日函數為

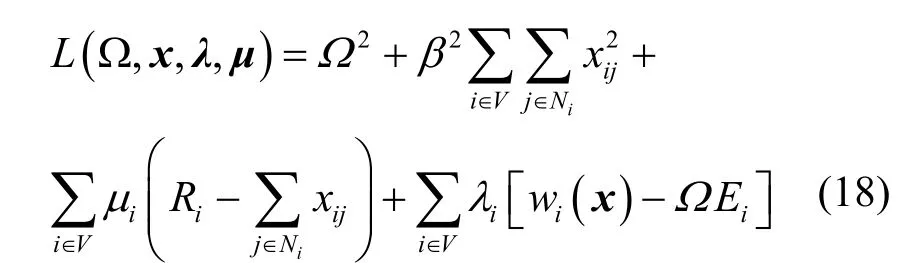
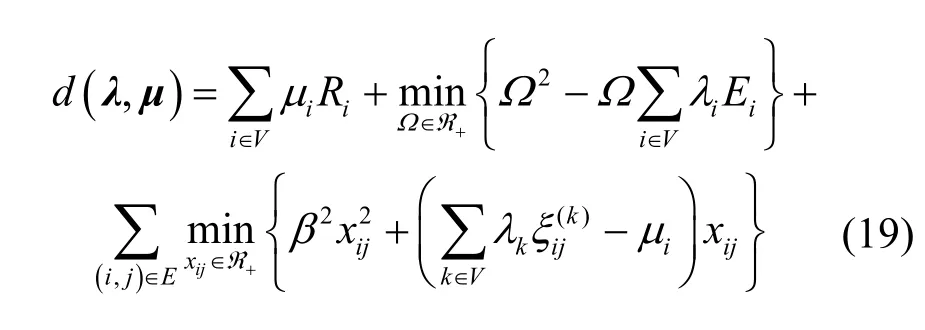
其中，()kijξ是式(8)中ijx的系數。于是得到如下序列

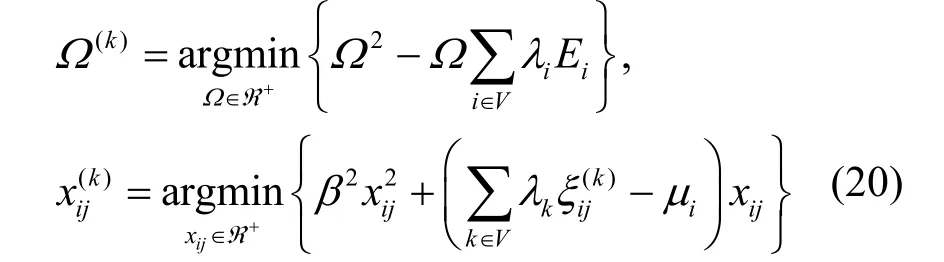
對偶函數 d （λ, μ ）在（λ(k), μ(k)）處的次梯度為

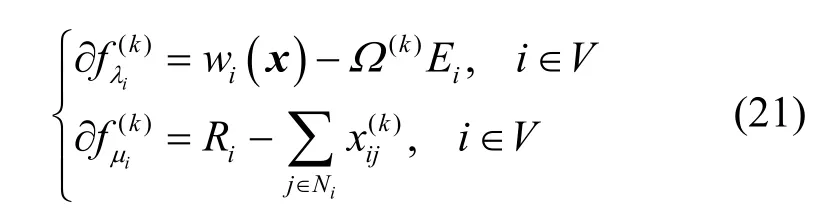
從上述可以得出問題的分布式算法。首先，通過分布式 Bellman-Ford[20]算法獲得網絡的最小生成森林，算法復雜度為 O (d|E | )，其中d是網絡的直徑。然后，由葉節點開始，根據式(7)遞推得到聚合數據流與原始數據流之間的相關系數 ζ（ij），于是得到式(8)中對應于 wk(x)中 xij的系數。此步驟的復雜度為然后根據式(20)和式(21)計算對偶問題的次梯度，并更新拉格朗日乘數。其中，式(20)的復雜度為式(21)的復雜度為重復迭代步驟，直到對偶問題的目標函數下降的相對幅度低于一個足夠小的門限。算法中只涉及到初等代數運算，實現復雜度較低。

6 仿真實驗

6.1 仿真場景

仿真采用MATLAB數學工具實現。50～120個節點與1～5個基站隨機分布在100m×100m范圍的矩形區域中。節點初始能量為 1kJ，數據產生率都是 1kbit/s，發射機功率增益路徑損耗系數η=2，電路驅動功耗數據相關系數α的取值范圍為 0 .001～0.01 /m2。分布式算法中，懲罰系數β=0.1。對每個網絡規模，產生 20個隨機生成的網絡拓撲，且所示結果都是各個場景結果的平均值。

6.2 網絡規模的影響

圖3所示為網絡生命期與網絡規模之間的關系。其中，數據相關系數 α = 0 .05 /m2。從圖3中可以看到，隨著網絡中節點數量的增加，網絡生命期也逐漸增加。隨著基站數量的增加，網絡生命期逐漸增加。同時，隨著基站數量的增多，新加入基站對網絡生命期的提升幅度逐漸減少。這是因為節點數量的增加，引起節點間距的縮短，有利于發射功率的降低以及數據相關性的提升，同時路由算法能夠有效地均衡節點數據流量負載，這些有利因素超過了網絡原始數據率增加所帶來的能耗增加，因而使得網絡生命期增加。而在網絡中引入新的基站，能夠減少節點與基站間的距離，減輕原生成森林上的數據流量，降低節點負載，提高網絡生命期。隨著基站數量的增大，新加入的基站只能影響鄰近基站的生成樹，對網絡的影響逐漸變小，因而對網絡生命期的提升效果逐漸減弱。

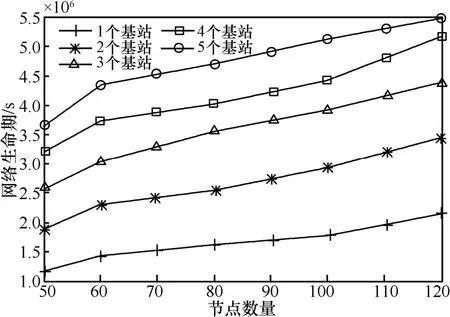
圖3 網絡生命期與網絡規模的關系

網絡平均能耗率與網絡規模的關系如圖 4所示。其中，網絡平均能耗率。隨著網絡規模的增加，節點平均能耗率呈下降趨勢。隨著基站的增加，網絡平均能耗率也逐漸降低。而當基站數量增多時，新加入基站對網絡平均能耗率的降低程度也減少。同樣的變化規律也能夠從圖 5所示的網絡聚合數據率與網絡規模的變化曲線上體現。

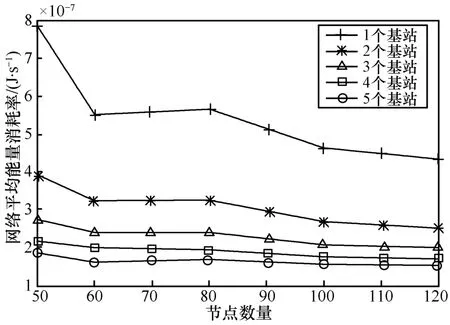
圖4 網絡平均能耗率與網絡規模的關系

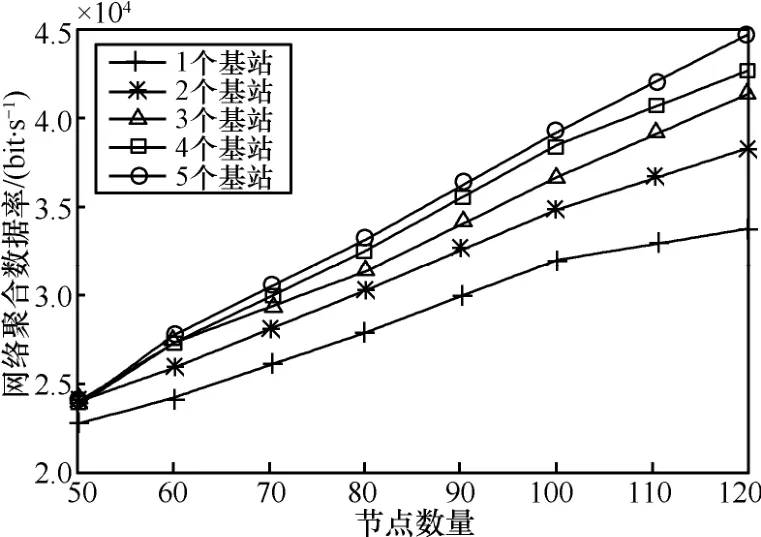
圖5 網絡聚合數據率與網絡規模的關系

6.3 數據相關性的影響

圖 6是網絡生命期與數據相關性的關系曲線圖。其中，網絡規模為100個節點。不難發現，當數據相關系數增加時，數據相關性逐漸降低，網絡中的數據流量變大，節點能耗增加，網絡生命期如圖中所示呈下降趨勢。由于節點被分布到以各基站為根的生成樹上，當基站數量增加時，生成樹數目增加，單棵樹上的節點數量減少，所承載的數據流量減少，節點能耗降低，因此網絡生命期也增大。當基站數量變多時，新加入的基站只能影響越來越少的已有生成樹，對網絡生命期的提高效果降低。這些變化規律從圖7的網絡平均能耗率與數據相關性的關系以及圖 8的網絡聚合數據率與數據相關性的關系中都有明顯的印證。

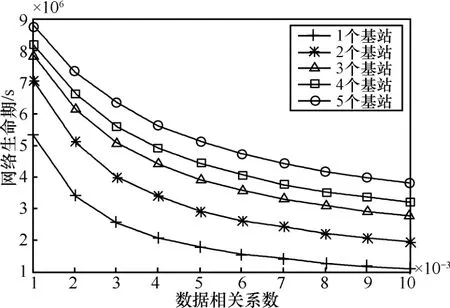
圖6 網絡生命期與數據相關性的關系

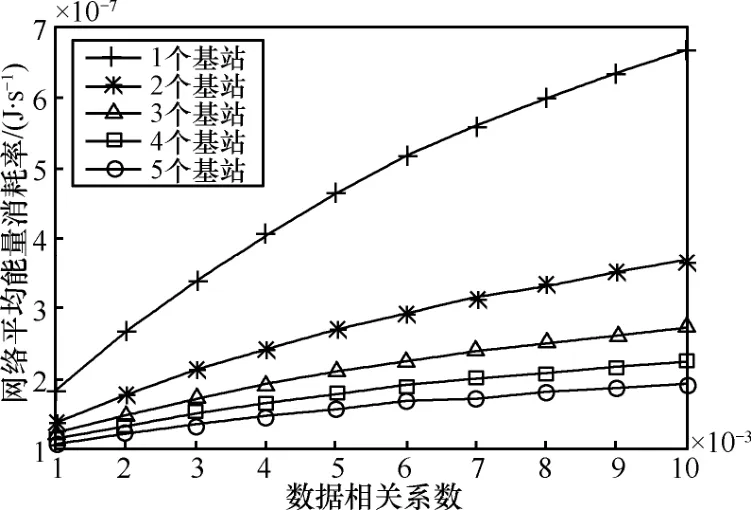
圖7 網絡平均能耗率與數據相關性的關系

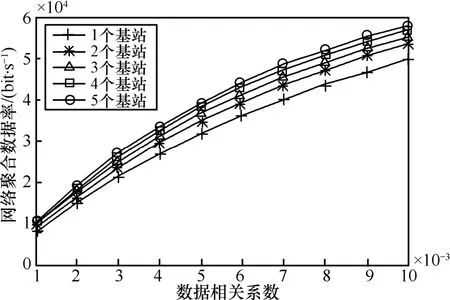
圖8 網絡聚合數據率與數據相關性的關系

6.4 分布式算法的收斂性能

圖9 表示的是120個節點的一個場景下，分布式算法的迭代收斂曲線。其中，歸一化的網絡生命期是通過式(20)迭代所得網絡生命期Ω的中間過程值與式(9)的最優解的比值。從圖中可以看到，算法在2 000次迭代內可以收斂到最優值的110%，在3 300次迭代內能夠收斂到最優值的105%。而且算法最終能夠相當準確地收斂到最優值。表1中是不同網絡規模下分布式算法的收斂性的數據。

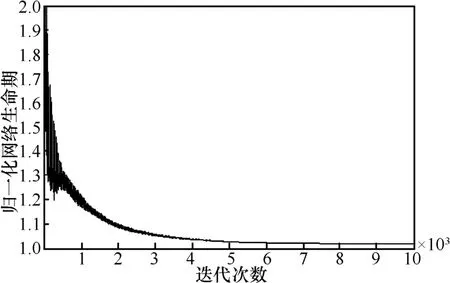
圖9 分布式算法的收斂性質

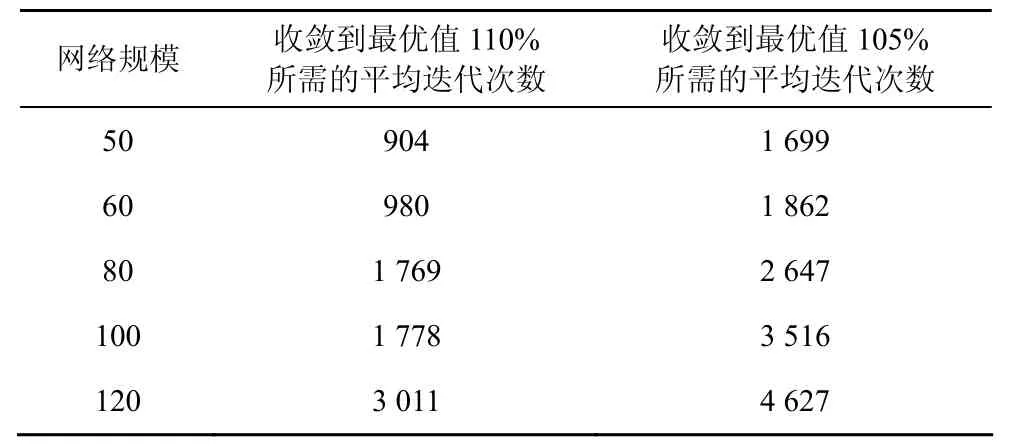
表1 不同網絡規模下分布式算法的收斂性能

7 結束語

本文對多基站無線傳感器網絡中的最大生命期路由算法進行了研究。本文首先證明了該類路由問題的NP-hard性質，然后提出了一種基于生成森林的啟發式路由算法，之后根據次梯度方法設計了分布式路由算法。本文通過大量的仿真實驗對啟發式算法的性能進行了分析，并表明所提分布式算法具有較好的收斂性能。

[1] AKYILDIZ I F, WEILIAN S, SANKARASUBRAMANIAM Y, et al.A survey on sensor networks[J]. IEEE Communications Magazine,2002, 40(8)∶ 102-114.

[2] YANG Y, KRISHNAMACHARI B, PRASANNA V K. Data gathering with tunable compression in sensor networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2008, 19(2)∶ 276-287.

[3] SONG L, KALOGERAKI V, GUNOPULOS D, et al. Online information compression in sensor networks[A]. IEEE International Conference on Communications (ICC’06)[C]. Istanbul, Turkey, 2006. 3371-3376.

[4] SONGHWAI O, SCHENATO L, CHEN P, et al. Tracking and coordination of multiple agents using sensor networks∶ system design, algorithms and experiments[J]. Proceedings of the IEEE, 2007, 95(1)∶ 234-254.

[5] LIANG S, DIMITRIOS H. A Cross-layer architecture of wireless sensor networks for target tracking[J]. IEEE/ACM Transactions on Networking, 2007, 15(1)∶ 145-158.

[6] AYSAL T C, BARNER K E. Blind decentralized estimation for bandwidth constrained wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2008, 7(5)∶ 1466-1471.

[7] MAY W, AKSOY D. Relative accuracy based location estimation in wireless ad hoc sensor networks[A]. IEEE International Conference on Communications (ICC’07)[C]. Glasgow, Scotland, 2007. 3244-3250.

[8] CHONG L, KUI W, JIAN P. An energy-efficient data collection framework for wireless sensor networks by exploiting spatiotemporal correlation[J]. IEEE Transactions on Parallel and Distributed Systems,2007, 18(7)∶ 1010-1023.

[9] VURAN M C, AKYILDIZ I F. Spatial correlation-based collaborative medium access control in wireless sensor networks[J]. IEEE/ACM Transactions on Networking, 2006, 14(2)∶ 316-329.

[10] HAN B, SIMON G. Fair capacity sharing among multiple sinks in wireless sensor networks[A]. IEEE Internatonal Conference on Mobile Adhoc and Sensor Systems (MASS’07)[C]. Pisa, Italy, 2007. 1-9.

[11] CRISTESCU R, BEFERULL-LOZANO B, VETTERLI M, et al.Network correlated data gathering with explicit communication∶NP-completeness and algorithms[J]. IEEE/ACM Transactions on Networking, 2006, 14(1)∶ 41-54.

[12] YUEN K, LIANG B, LI B. A distributed framework for correlated data gathering in sensor networks[J]. IEEE Transactions on Vehicular Technology, 2008, 57(1)∶ 578-593.

[13] VURAN M C, AKAN O B. Spatio-temporal characteristics of point and field sources in wireless sensor networks[A]. IEEE International Conference on Communications (ICC’06)[C]. Istanbul, Turkey, 2006.234-239.

[14] SEUNG JUN B, GUSTAVO DE V, XUN S. Minimizing energy consumption in large-scale sensor networks through distributed data compression and hierarchical aggregation[J]. IEEE Journal on Selected Areas in Communications, 2004, 22(6)∶ 1130-1140.

[15] ANANDKUMAR A, LANG T, SWAMI A, et al. Minimum cost data aggregation with localized processing for statistical inference[A]. The 27th IEEE Conference on Computer Communications (INFOCOM’08)[C]. Phoenix, AZ, USA, 2008. 780-788.

[16] YOUNGCHUL S, SASWAT M, LANG T, et al. Cooperative routing for distributed detection in large sensor networks[J]. IEEE Journal on Selected Areas in Communications, 2007, 25(2)∶ 471-483.

[17] HEINZELMAN W B, CHANDRAKASAN A P, BALAKRISHNAN H.An application-specific protocol architecture for wireless microsensor networks[J]. IEEE Transactions on Wireless Communications, 2002,1(4)∶ 660-670.

[18] YAN W, FAHMY S, SHROFF N B. On the construction of a maximum-lifetime data gathering tree in sensor networks∶ NP-completeness and approximation algorithm[A]. The 27th IEEE Conference on Computer Communications (INFOCOM’08)[C]. Phoenix, AZ, USA,2008. 356-360.

[19] BAVISH B. Formulations and algorithms for the capacitated minimal directed tree problem[J]. Journal of the ACM, 1983, 30∶ 118-132.

[20] CORMEN T H, LEISERSON C, RIVEST R L, et al. Introduction to Algorithms[M]. Cambridge, MA∶ MIT Press, 2001.

[21] LIN F Y S, YEAN-FU W. Multi-sink data aggregation routing and scheduling with dynamic radii in WSNs[J]. IEEE Communications Letters, 2006, 10(10)∶ 692-694.

[22] MADAN R, LALL S. Distributed algorithms for maximum lifetime routing in wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2006, 5(8)∶ 2185-2193.

[23] KIM S, AHN H. Convergence of a generalized subgradient method for nondifferentiable convex optimization[J]. Mathematical Programming,1991, 50(1-3)∶75-80.

[24] LUENBERGER D, YE Y. Linear and Nonlinear Programming[M]. 3rd edition. New York∶ Springer-Verlag, 2008.