一種新的幾何約束系統參數取值范圍的計算方法

張杏莉， 胡運紅， 盧新明

（山東科技大學信息科學與工程學院，山東 青島 266510）

一種新的幾何約束系統參數取值范圍的計算方法

張杏莉， 胡運紅， 盧新明

（山東科技大學信息科學與工程學院，山東 青島 266510）

在利用參數化CAD系統進行圖形設計的過程中，通過修改圖形對象的可變參數重新生成圖形是最常見的一種操作。但用戶在改變參數的過程中，由于事先并不知道有效的參數值，也沒有任何引導信息，導致了用戶只能盲目地不斷輸入參數值，通過反復輸入參數值來滿足約束關系的需要。該文將結構約束引入參數有效取值范圍求解的范疇，并提出了確定一類常用的二維參數化CAD模型中參數的有效范圍的計算方法和算法。算法復雜度為O(n2) 。

計算機輔助設計；參數CAD；參數取值范圍；幾何約束；方位約束；結構約束

CAD軟件的參數驅動原理是通過修改圖形對象的參數或標注尺寸來改變圖形對象的定位及尺寸，重新生成所需圖形。參數驅動技術是參數化、變量化的繪圖系統的核心技術，采用該設計方法，可以快速有效地進行產品開發。在這些軟件中保證圖形對象間拓撲結構不變的情況下改變圖形參數的值并重新生成幾何圖形是最常見的操作，但用戶在設計過程中經常會遇到參數驅動失敗的情況，這是因為用戶事先并不知道正確的參數值而給出了錯誤的或非法的參數值，這在一定程度上降低了產品開發的效率，增加了開發的難度。如圖1所示，圖1(a)表示C3與C1、C2內切，其中C3的約束為與C1、C2內切，參數為半徑，此時 C3的半徑應滿足C3R<(C1R+C2R-D12)/2（其中C1R表示C1的半徑，C2R表示 C2的半徑，C3R表示 C3的半徑，D12表示C1和C2圓心點間的距離）；圖1(b)表示在給C3半徑重新賦值時生成的新的幾何實體，此時，C3的約束仍為與C1、C2內切，但新生成的幾何實體的拓撲形狀發生了改變，此時C3R>(D12+C1R+C2R)/2；而當給C3半徑的賦值處于區間((C1R+C2R-D12)/2, (D12+C1R+C2R)/2)時，C3不存在，則直接導致幾何實體發生改變。

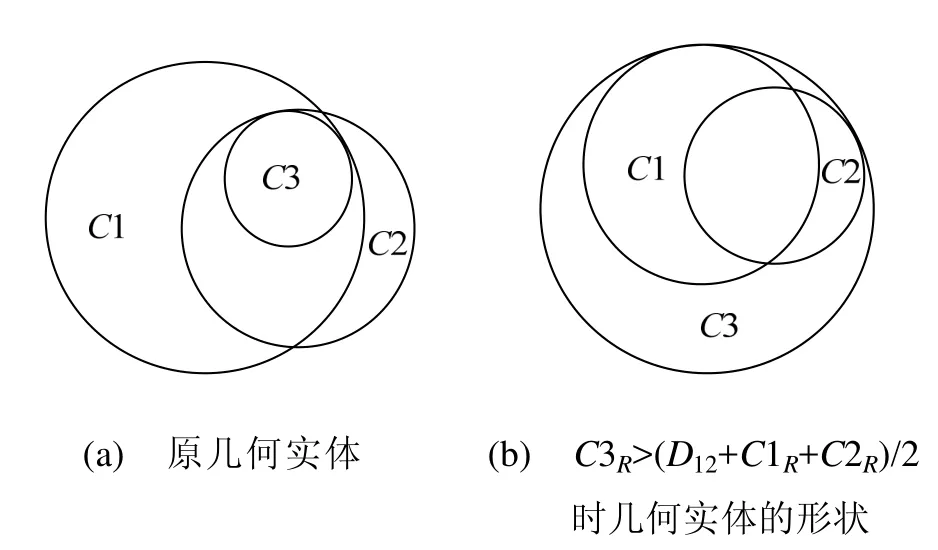
圖1 幾何實體重建失敗

幾何實體重建失敗一方面可能是由于該幾何實體參數化設計模型本身導致的；另一方面可能是由于不合理的重建計劃造成的；同時還有可能是由于前兩個方面同時造成的。這常常給設計者在診斷一個幾何實體重建失敗的原因時，造成很大的麻煩[1]。因此，如果在用戶改變某個參數值之前，參數繪圖系統自動給出該參數的有效取值范圍，將會大大提高設計的效率，降低設計的難度，也增加軟件的人性化和智能化程度。因此，實時地給出當前參數的正確取值范圍就成為一個新的急需解決的問題。

Hoffman和Kim[2]在二維環境中對只包含水平線段和垂直線段的閉合、不自交、良約束的直線多邊型做了一些研究, 并只允許包含水平方向和垂直方向的距離約束。他們確定了在保證線段間拓撲結構不變的情況下相關直線上下移動的范圍，另外，他們還指出了同一時間只能考慮一個距離參數的取值范圍。

蔣鯤等[1]人將幾何實體限制為只包含水平直線和垂直直線的封閉且不自交的矩形，將要求的參數限制為水平的距離約束和垂直的距離約束，給出了求解每個參數有效取值范圍的代數算法。

Joan-Arinyo等[3]對于尺規可構造性問題給出了有效的方法。Hilderick A.Van der Meiden和Willen F.Bronsvoort[4]提出的求解方法考慮了三維環境中基于點的距離約束和角度約束的良約束幾何約束系統，他們將幾何約束系統中的幾何實體分解成三角形和四面體子問題，在計算某個距離約束參數的取值范圍時，找出問題的退化子問題并根據退化子問題求出參數的臨界值。

在文獻[1-4]中都只考慮了距離約束和角度約束，均為尺寸約束，還沒有考慮結構約束，本文中，筆者將幾何實體增加到直線和圓，另外還將考慮一種最基本也是最常用的結構約束，即相切約束。

1 提出問題

本文考慮的參數模型中包含線段和圓，另外還將考慮一種結構約束即相切約束。從數學的角度來看，每一個幾何約束都可以用一組方程組來求解[5]。因此，要獲得整個幾何約束模型的解，需要解大量的方程組。最終的目的是得到一個想要的解，所以從大量的非線性方程組的解中選擇一個符合設計者設計意圖的解就成了最關鍵的問題。然而，當圖形元素不斷增加，幾何約束的個數不斷增多，圖形對象不斷復雜化，方程組的解則以指數級增長，從中選擇一個滿意的解很有可能變成一個NP問題[6]。

在作者的系統中，通過使用附加的方位約束來解決根的選擇問題。例如，已知半徑過圓外一點做與圓外切圓時，可以得到滿足條件的兩個解C1和C2，系統根據用戶的交互信息獲取用戶的設計意圖從而選擇其中一個解，同時為此圓附加方位約束值。如圖2所示，可以根據生成圓的圓心相對于點P與已知圓C的圓心的連線的位置來區分這兩個外切圓，若選擇 C1，為其附加的方位約束值為“outeleft”，若選擇C2，為C2附加的方位約束值為“outerigh”。

本文只考慮二維環境中給定包括直線段和圓的參數化模型，如何確定模型中圓的半徑參數的有效取值范圍，使得設計者只要在給定的有效范圍內賦值，就會得到有效的、不改變原有模型的拓撲形狀的新的圖形。

畫圓的方法很多，在表1中對畫圓方法進行歸類。

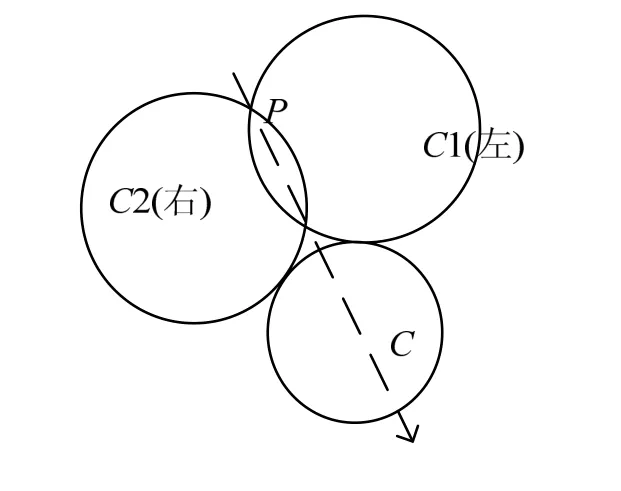
圖2 過P點做與圓C外切的圓

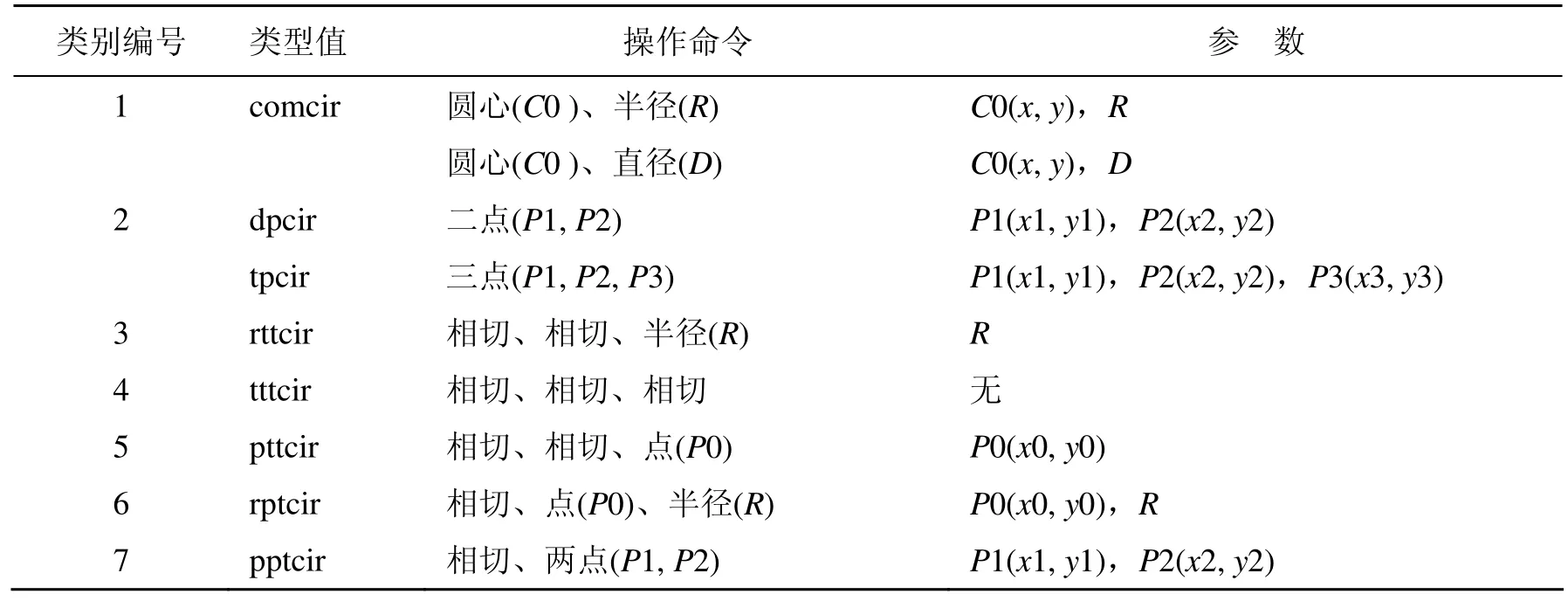
表1 畫圓方法歸類

對于上述問題，使用筆者創建的LK參數繪圖系統建立的參數化模型是完整約束的，因此不需要考慮過約束或者是欠約束的情況[7]。

2 參數取值范圍計算方法及算法

一個幾何實體的完整約束的參數化模型(WCPM)可以描述為：WCPM = (G，R)，其中G ={(g，s)| g為幾何實體（線、圓、非特征點），s為g的方位約束值}；R = {GR}，GR = { |i≠j且gi，gj兩者之間存在的約束關系，其中 gi對gj的位置或大小有約束關系}。

在參數驅動過程中將借助有向約束圖來完成判斷需要重新計算和定位的圖形對象，下面對有向約束圖的生成過程做簡單敘述。

在繪圖的過程中，根據操作命令和交互信息自動獲取設計約束，并將該設計約束轉化為有向圖的邊，也就是說，每生成一個圖形元素，對相關的設計約束進行處理，生成相應的有向邊，有向邊指向新生成的圖形元素，有向邊的尾部和與新生成的圖形元素有約束關系的已經繪制的圖形元素相連接，即WCPM中每一個GR關系都可以轉化成有向約束圖中的一條有向邊。

在有向約束圖中，規定圖素的特征點不能作為結點出現在有向約束圖中，而一般意義上的點除外。從這一點來看，使用該方法生成的有向約束圖中結點的類型和文獻[5]中的約束圖結點的類型有一定的區別。例如，線段的兩個端點在本文中作為特征點來處理，不出現在有向約束圖中，而在文獻[5]中，線段的端點是約束圖中的結點。

有向約束圖中每個結點的父結點為該結點依賴的所有前驅結點，也是約束計算的前提條件，對于二維環境中的參數化模型，每個結點最多只有三個父親結點；每個結點的子孫結點是指從當前結點出發與當前結點存在簡單路徑的所有結點。

另外，每一個幾何實體的方位約束值都有非常重要的作用，在本文中，方位約束值有兩個用途，第一，解決了根的選擇問題；第二，可以使自身及其它圖素的半徑參數的有效范圍更加的精確。如圖3所示，其中C1的圓心坐標為(300,200)，半徑為50，C2的圓心坐標為(350, 150)，半徑為80，做與C1、C2內切，半徑為20的圓C3，此時，圓C3的約束為與C1、C2分別內切，參數為半徑，根據交互信息獲取設計者意圖并自動為C3添加方位約束值為“rightlitt”，它的意思是該圓位于C2、C1兩圓圓心連線的右側，且該圓為半徑小于任何一個內切圓的小圓，該模型的當前有向約束圖如圖4所示。在不加方位約束的情況下求解 C3的半徑的取值范圍，得到(0,29.64466]，在添加方位約束情況下，半徑的有效取值范圍為(0, 29.64052]，保證了C3的圓心點在C2與C1圓心連線的右側，可見方位約束是算法中必不可少的內容。

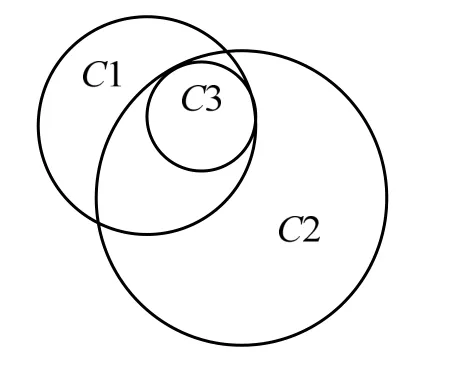
圖3 與C1、C2內切的圓C3

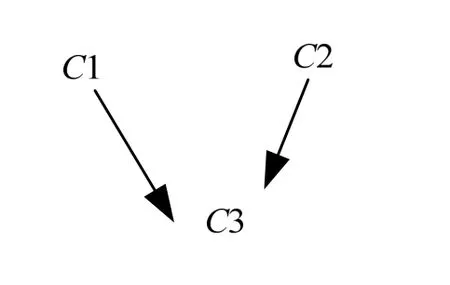
圖4 圖3的有向約束圖

下面的算法中將討論如何確定模型中圓的半徑參數的有效取值范圍。

算法1 參數化模型中圓的半徑參數的有效范圍的確定算法

輸 入 某圓的ID號

輸 出 該圓的半徑取值范圍

第一步 判斷該圓的半徑是否為參數，如果是，轉第二步，否則，退出；

第二步 根據該圓的ID號獲取類型值，設其ID號為L，并將該圓記為CL，則假設該圓圓心坐標為(CLX, CLY)，半徑為CLR，根據有向約束圖，得到指向該圓的父結點的 ID號，根據父結點個數及每個父結點的ID號利用算法2列出方程組，再根據該圓的 ID號及方位約束值，再次利用算法2列出方程組，轉第三步；

第三步 根據有向約束圖，得到該圓的子孫結點所表示圖素ID號、類型和方位約束值，再獲取每一個子孫結點的父結點個數及ID號，再反復利用算法2列出方程組，與第二步所得的方程組聯立組成一個大的方程組；

第四步 用擬牛頓法解此聯立方程組，求CLR的最大值UR和最小值LR；

第五步 將該半徑的有效取值范圍(UR, LR]輸出在繪圖系統的狀態顯示區。

算法2 根據所求圖素ID號，父結點ID號、方位約束值，列出對應方程組

輸 入 所求圖素ID號，父結點ID號、方位約束值

輸 出 方程組

第零步 設所求圖素 ID號為 L，且該圖素為圓，則假設該圓圓心坐標為PC(CLX, CLY)，半徑為CLR，若所求圖素為線段，則返回；

第一步 若所求圖素ID號，父結點ID號不為空，方位約束值為空，則轉第二步；若所求圓ID號和方位約束值不為空，則轉第三步；否則，返回；

第二步 若所求圖素的父結點為圓，其 ID號為K，設其圓心為(CKX, CKY)，半徑為CKR；若父結點為直線段，設該直線的ID號為K，直線方程式為aK*x+bK*y+cK= 0；若父結點為普通點或為某一圖素的特征點，設點ID號為K，則設該點坐標為(PKX, PKY)；

若該圖素為點，則有兩種可能，第一，點在圓上，則方程式為(CLX-PKX)^2+(CLY

-PKY)^2 =CLR^2；第二，點為所求圓的圓心，則所求圓的圓心坐標(CX, CY)確定，即添加方程式CLX= PKX，CLY= PKY，返回；

ABS(aK*CLX+bK*CLY+cK)/((aK*aK+bK*bK)^0.5)=CLR，返回；

若該圖素為圓，則有兩種可能，第一，兩圓外切，則方程式為：(CLX-CKX)^2+(CLY-CKY)^2 =(CLR+CKR)^2；第二，兩圓內切，則方程式為：(CLX-CKX)^2+(CLY-CKY)^2 =(CLR-CKR)^2，返回；（其中的未知量僅為所求圓圓心(CX, CY)及半徑CR，其余均為已知量）

第三步 若父結點 ID號為空，將參數方位約束值轉換成相應方程組（只有圓有方位約束值）。

若圓類型為comcir、dpcir、tpcir，則該圓沒有方位約束值，返回；

所求否則，若方位約束值中包括righ或left，則：

（1） 圓位于一條有向線段的右側或左側；

（2） 圓位于某圓圓心到某條線段的垂線的右側或左側；

（3） 圓位于兩圓圓心連線的右側或左側。

星雨將“石壓蛤蟆”“死蚯蚓”“大道曰返”講給李離聽，李離也笑得前仰后合，一邊又正色對星雨講：“顏老師的字雄秀獨出，一變古法，兼收漢魏晉宋以來風流，我朝書法名家，沒有誰超過他的。字如其人，他格力天縱，神乎其神，難以預測！練百花拂穴手中的‘快雪時晴’‘鐘林毓秀’，都應體會書圣的筆意！”星雨聽得半懂不懂，只是覺得顏師父的課雖然沒什么意思，但這些促狹師兄太有意思了……

計算出有向線段的起點坐標PS(SX, SY)、終點坐標PE(EX, EY)、PSPE與X正軸的夾角A1，A1∈[0°,360°), A1=ATN((EY-SY)/(EX-SX))(設 EX≠SX)。

若為 righ，則(CLY-SY)*COS(A1)-(CLX-SX)*SIN(A1)<0；

若為 left，則(CLY-SY)*COS(A1)-(CLX-SX)*SIN(A1)>0；

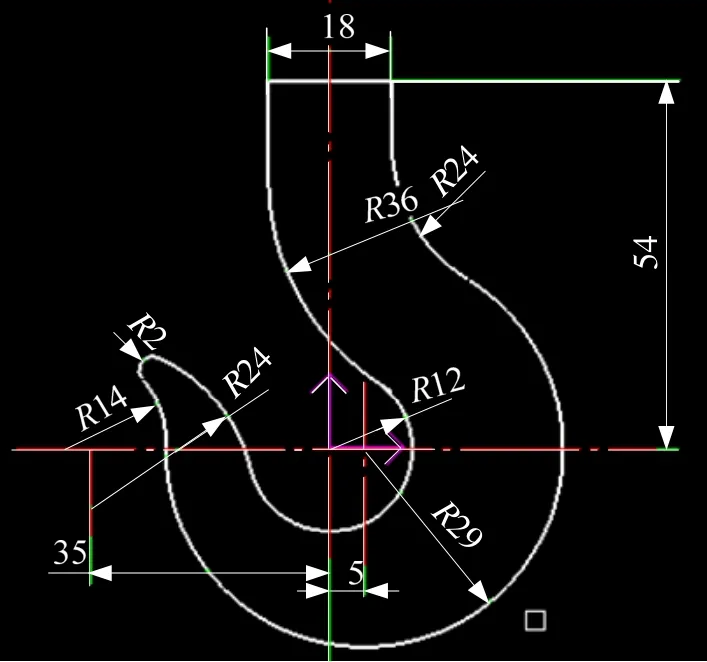
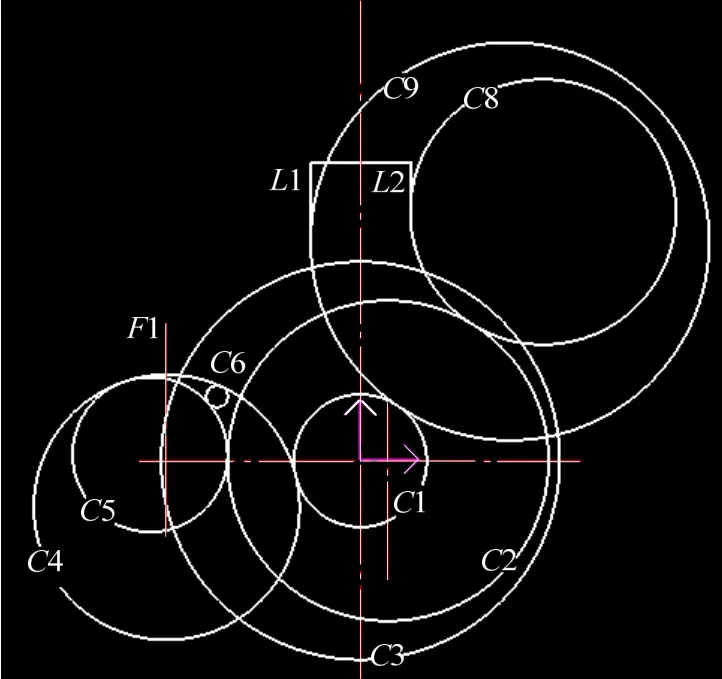
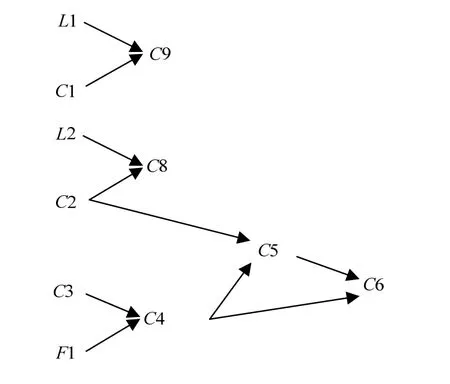
若方位約束值中包括 litt，則表示該圓為內切于其它圓的小圓，即該圓的半徑小于任何一個內切圓，此時添加方程式：(CLX-CMX)^2+(CLY-CMY)^2

若方位約束值中包括bigg，則表示該圓為內切于其它圓的大圓，即該圓的半徑大于任何一個內切圓，此時添加方程式：(CLX-CMX)^2+(CLY-CMY)^2>CMR^2，其中 M 為這些內切圓中半徑最大的圓的ID號；

若方位約束值中包括inne，則表示該圓和另一個圓為內切關系，則添加方程式：(CLX-CKX)^2+(CLY-CKY)^2

3 實 例

圖5所示的吊鉤是一個非常不規則的零件，圓弧連接比較多，在畫圖過程中，要借助多個圓并使用裁剪功能后得到最終零件圖。圖5給出了吊鉤的尺寸標注及最終零件圖，圖6所示為做圖過程，圖中的所有圓都給了相應的標識，其中C3的圓心坐標為(0, 0)，半徑為36。下面就以此例來說明在參數驅動過程中圓C5的半徑取值范圍。

圖5 吊鉤

圖6 圖5的做圖過程

圖7 圖5的有向約束圖

根據上述有向約束圖的生成方法，圖5所示吊鉤的有向約束圖如圖7所示。下面根據算法來求C5的半徑取值范圍。

輸 入 ID = 5

第一步 該圓的做圖方法為：相切、相切、半徑，半徑是參數，轉第二步；

第二步 當前所求圓ID號為5，該圓類型為rttcir，方位約束值為inneouteleft，設其圓心為(C5X,C5Y)，半徑為C5R, C5的父結點的ID號分別為2和4，則3次調用算法2：

（1） 父結點 ID號為 2，其圓心設為(C2X,C2Y)，半徑為C2R，該父結點為圓，且C2與C5為外切關系，得方程式(C5X-C2X)^2+ (C5Y-C2Y)^2= (C5R+C2R)^2，其中 C2X、C2Y、C2R均為己知量，如圖5所示，其中C2X= 5，C2Y= 0，C2R= 29。

（2） 父結點 ID號為 4，其圓心設為(C4X,C4Y)，半徑為C4R，該父結點為圓，且C4與C5為內切關系，得方程式(C5X-C4X)^2+(C5Y-C4Y)^2= (C5R-C4R)^2，其中C4X、C4Y是輔助線F1：X =-35與圓C3的第二個交點，計算可知，C4R為己知量，C4X=-35，C4Y=-8.4261，C4R= 24。

（3） 此時父結點ID號為空，轉算法2的第三步，將C5的方位約束值轉為相應方程式。C5的約束方位值為包含了 inne，增加方程式：(C5X-C4X)^2+(C5Y-C4Y)^20。

此時所得方程式如下：(C5X-C2X)^2+(C5Y-C2Y)^2 = (C5R+C2R)^2；C2X= 5；C2Y= 0；C2R=29；(C5X-C4X)^2+(C5Y-C4Y)^2=(C5R-C4R)^2；C4X=-35；C4Y=-8.4261；C4R=24；(C5X-C4X)^2+(C5Y-C4Y)^20。

第三步 C5的子孫結點為C6，C6為當前所求圓，其ID號為6，類型值為rttcir，方位約束值為inneouterigh，因為該子孫結點為圓，因此設其圓心坐標為(C6X, C6Y)，半徑為C6R，并從有向約束圖中得知其父結點為C5和C4，也會三次調用算法2：

（1） 父結點 ID號為 4，其圓心設為(C4X,C4Y)，半徑為C4R，該父結點為圓，且C4與C6為內切關系，得方程式(C6X-C4X)^2+(C6Y-C4Y)^2= (C6R-C4R)^2，其中 C4X= -35，C4Y= -8.4261，C4R= 24。

（2） 父結點 ID號為 5，其圓心設為(C5X,C5Y)，半徑為C5R，該父結點為圓，且C6與C5為外切關系，得方程式(C6X-C5X)^2+(C6Y-C5Y)^2= (C6R+C5R)^2，另外C6R= 2。

（3） 此時父結點 ID號為空，轉算法二的第四步，將C6的方位約束值轉為相應方程式。C6的約束方位值為包含了 inne，增加方程式：(C6X-C4X)^2+(C6Y-C4Y)^2

第三步所得方程式如下：(C6X-C4X)^2+(C6Y-C4Y)^2=(C6R-C4R)^2；(C6X-C5X)^2+(C6YC5Y)^2=(C6R+C5R)^2；C6R=2；(C6X-C4X)^2+(C6Y-C4Y)^2

第四步 聯立第二步和第三步所得方程式，用擬牛頓法求解C5R的最大值和最小值，最終得到C5的半徑 C5R的取值范圍為(0,17.90074]。

第五步 將該半徑的有效取值范圍(0,17.90074]輸出在繪圖系統的狀態顯示區，讓設計者參考。

經實驗證明，圓C5的半徑參數在(0,17.90074]范圍內取任何一個值都可以保證模型中各圖形間約束關系、拓撲形狀不發生改變，而在這個范圍之外的數值則會導致模型重建失敗。

4 結 束 語

為了避免在參數驅動時由于賦值的不合理而導致的幾何實體重建失敗的情況，本文提出了一個解決算法，對于二維環境中的包括線段和圓的良約束幾何約束系統，給出了二維參數化模型中圓的半徑參數的有效取值范圍的計算方法，在給定的取值范圍內任何一個值都保證在約束關系、拓撲形狀不變的情況下得到一個想要的解。

本文提出的算法不僅適用于計算繪圖過程中當前繪制的圓的半徑的有效取值范圍，也適用于參數驅動過程中圓的半徑的有效取值范圍，另外，使用多次該算法可以同時計算出當前模型中所有半徑的有效取值范圍。

[1]蔣 鯤, 朱長才, 高小山. 參數化 CAD中參數的有效范圍[J]. 計算機輔助設計與圖形學學報, 2003,15(8)：1016-1020.

[2]Hoffmann C M, Kim K –J. Towards valid parametric CAD models [J]. Computer-Aided Design, 2001, 33：81-90.

[3] Joan-Arinyo R, Mata N. Applying constructive geometric constraint solvers to geometric problems with interval parameters [J]. Nonlinear Analysis, 2001,47：213-224.

[4]Hilderick A Van der Meiden, Willem F Bronsvoort. A constructive approach to calculate parameter ranges for systems of geometric constraints [J]. Computer-Aided Design, 2006, 38：275-283.

[5]fudos I, Hoffmann C M. A graph-constructive approach to solving systems of geometric constraints [J]. ACM Transactions on Graphics, 1997, 16(2)：179-216.

[6]Mata N, Kreinovich V. NP-hardness in geometric construction problems with one interval parameter [C]//Applications of Interval Analysis to Systems and Control with Special Emphasis on Recent Advances in Modal Interval Analysis (MISC'99), Girona(Spain),1999：85-98.

[7]孟祥旭, 汪嘉業, 劉慎權. 基于有向超圖的參數化表示模型及其實現[J]. 計算機學報, 1997, 20(11)：982-988.

A New Approach to Calculating Parameter Ranges for Systems of Geometric Constraints

ZHANG Xing-li, HU Yun-hong, LU Xin-ming
( College of Information Science and Engineering, Shandong University of Science and Technology, Qingdao Shandong 266510, China )

In parametric CAD graphic design, it is a common operation to modify the parameters of graph objects to regenerate graphics. Users usually need to repeatedly enter parameter values in the geometric constraint system to get a satisfactory solution. In the process of changing the value of parameters, the allowable parameter values are not known to the user beforehand and there is no guide information, so users have to input the parameter values in a trial-and-error way. This paper introduces structural constraints to the field of interval parameters and proposes an algebraic algorithm for determining the valid ranges of parameter values. The complexity of the algorithm is O(n2).

computer aided design; parametric CAD; parameter ranges; geometric constraints; position constraints; structural constraints

TP 391

A

1003-0158(2010)06-0085-07

2009-01-08

張杏莉（1981-），女，山西芮城人，講師，博士研究生，主要研究方向為計算機輔助軟件工程，計算機圖形學。

book=6,ebook=123