基于剛柔結合建模技術的道岔區輪軌動力學仿真分析

羅雁云 譚大正 施董燕

(同濟大學鐵道與城市軌道交通研究院,201804,上海∥第一作者,教授、副院長)

道岔是軌道交通設備中的重要組成部分,同時也是軌道交通中最薄弱的環節之一。道岔區軌下不平順會加劇列車過岔時的輪軌相互作用,降低列車運行的平順性,從而導致道岔使用壽命的縮短。因此,為了提高列車過岔安全,改善列車運行的平順性,有必要開展對道岔結構的動力學研究,而仿真分析是其中重要的技術手段之一。

過去在對車輛-軌道耦合系統進行動力學分析時,通常把車輛和軌道假設為剛性體,在此前提下建立的多剛體運動模型具有局限性,與實際情況有較大差異。事實上,鋼軌本身的材料和結構具有彈性。在耦合系統中,鋼軌一方面繞固定坐標系運動,另一方面相對自身局部坐標系做彈性變形運動,具有柔性體的特性。本文將主要研究對象道岔區的鋼軌視作柔性體,次要對象車輛視為剛性體,利用耦合技術進行系統動力學仿真;目的是反映軌道結構柔性結構特征對整個車輛-道岔系統的影響,同時保留車輛為剛體,以減少求解難度、簡化模型、提高仿真結果的精度。

1 車輛-道岔剛柔結合系統模型

1.1 剛柔體結合理論原理

運用有限元軟件和多體動力學軟件聯合仿真創建剛柔結合系統模型。即在系統中將所關心的對象柔性化,以有限元方式創建一個仿真模型,然后將其模態分析結果與剛體模型集成。

通常采用兩個坐標系描述多體系統中柔體的運動：一是慣性坐標系,另一是固定于柔性體上的局部坐標系。因此柔體中任意點P的運動為：

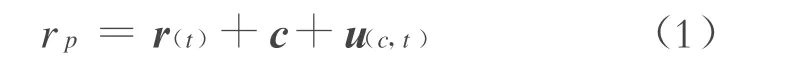
其中：r(t)和c是剛體運動矢量;u(c,t)是變形矢量,其Ritz近似為[1-2]：

其中：u(c,t)是模態振型uj(c)與模態坐標qj(t)加權的線性組合。模態振型 uj(c)可由有限元軟件計算的固有特征振型與在靜態載荷和約束作用下的靜變形-靜態振型內插得到,即：

為滿足MBS(多體系統)方程的要求,需把柔體通過式(2)轉化為彈性體運動方程：

式中：

b——加速度向量;

ω——旋轉加速度;

q——變形加速度;

r——柔體上某單元相對局部坐標系原點的位置矢量;

M——慣性(質量)矩陣;

Kω(ω,q,q?)— —阻尼向量陣;

K(q)——剛度向量陣;

h(r,q,…)——廣義力向量陣。

其中加速度向量b由平動加速度a、旋轉加速度 ω和變形加速度q三部分構成。因此產生的MBS方程所要求的柔體數據是必須計算的質量陣、阻尼陣和剛度陣。這些數據可預先進行計算,形成相應的標準輸入數據文件以備使用。彈性體運動方程中的系數矩陣通過標準輸入數據文件被傳遞給多體程序。也正是該文件提供的彈性體數據以及模態計算結果,才可以執行后續的整個運動方程的建立及進行多體系統仿真分析。

1.2 計算模型

本文以12號道岔為例,其轍叉區如圖1所示。

圖1 12號道岔可動心軌轍叉區結構示意圖

在有限元軟件和多體動力軟件中,所創建的車輛-道岔耦合系統主要包括以下三部分：道岔區的軌道模型、車輛模型、輪軌接觸模型。通過導入不平順激擾模型,分析動荷載作用下軌道動力特性及軌下動剛度分布規律。

首先在PATRAN軟件中創建道岔區的軌道模型,將其假定為均勻變截面梁(鋼軌截面模擬為工字梁,如圖2所示);計算模型的各階固有頻率,得到柔性體模態中性文件(*.mnf文件)。本文采用輸出自由模態200階,將結果導入ADAMS軟件后發現同樣受力方式下模型的變形與在PAT RAN軟件中的變形能夠很好地吻合,符合計算精度要求。

圖2 變截面鋼軌有限元模型

在ADAMS軟件中建立車輛-道岔系統模型,車輛簡化為帶單個轉向架的半車模型,包括車體、轉向架、輪對、一系懸掛系統、二系懸掛系統。導入已生成的鋼軌模態中性文件,生成道岔區軌道柔性體模型。

在剛柔結合模型中,如何處理剛性體和柔性體的接觸問題是關鍵技術之一。在本文模型中,通過引入虛構件來解決。虛構件是一種質量和轉動慣量都為零的剛體,沒有任何質量信息,不會對模型的計算結果帶來影響,但是可以解決ADAMS軟件中柔性體和剛性體之間不能進行柔性連接的模型問題。本模型運用車輪與虛構件接觸連接、虛構件與軌道單元固結的方式,簡化了輪軌接觸方式。接觸形式使用碰撞函數Impact表示,非線性彈簧參數k=1×1012N/m,阻尼參數 cmax=1×104N。

1.3 道岔轍叉區軌下不平順

研究在不平順激擾下車輛通過道岔區時的軌道動力特性。不平順在模型中是否恰當表達,對最后結果的輸出分析有直接的影響。道岔區存在不平順主要是指復雜的結構造成的幾何不平順以及軌下剛度不平順。幾何不平順在道岔心軌區較為明顯。根據《道岔設計手冊》,將在豎直面上出現的幾何不平順在模型中采用縱向L=0.8 m、豎向h=3 mm的三角體來模擬,如圖3所示。

圖3 幾何不平順簡化模型

道岔轍叉區軌道剛度不平順是指軌道豎向剛度大且沿縱向分布不均勻,在轍叉、心軌等部位的軌道剛度呈跳躍性變化。隨著列車速度的提高,道岔轍叉區軌道剛度的嚴重不均勻加重了道床及道岔部件的損傷。根據軌道剛度分布規律[3],道岔中的連接軌主要有三個剛度突變點,最大值達256 kN/mm。本文采取彈性元件阻尼器的剛度輸入法來模擬剛度不平順,不僅能直觀地輸入軌道豎向剛度值,而且通過設置移動特性的橫向和縱向剛度最大值、轉動特性的三向剛度最大值,而使軌道在動力仿真過程中保持橫向、縱向和轉動的穩定性,為研究道岔豎向剛度不平順對整個輪軌系統的動力特性提供了條件。

2 動力學仿真及結果

2.1 不同速度通過道岔轍叉區對系統動力特性的影響

圖4和圖5分別為車輛以200 km/h的速度直向通過道岔時,心軌尖端輪下鋼軌豎向振動和豎向位移。圖4、5中的兩個峰值,分別是兩對車輪前后通過心軌尖端所產生的軌道振動和位移。可見心軌尖端輪下鋼軌最大振動加速度為948 m/s2,豎向位移為0.95 mm。由此可知,車輛通過道岔時,由于心軌尖端剛度大且存在幾何不平順,振動比較劇烈,在設計中,應保證此處的豎向穩定性,防止鋼軌傾覆。

圖4 道岔心軌尖端處輪下鋼軌豎向振動加速度

表1所示為該模型在列車 120、160、200、250 km/h速度下直向過岔時,基本軌、連接軌和心軌尖端的豎向位移和豎向加速度的最大值。比較同一速度下基本軌和連接軌的最大加速度,基本軌的最大豎向位移大于連接軌的最大豎向位移,基本軌的最大豎向加速度小于連接軌的最大豎向加速度。當列車直向過岔速度為200 km/h時,連接軌加速度比基本軌豎向加速度高出4.5%。從圖6和圖7也可以看出,隨著車輛過岔速度的增大,基本軌、心軌尖端的豎向加速度接近于連接軌最大豎向加速度。當過岔速度為250 km/h時,基本軌最大豎向加速度比200 km/h時增大約40%,連接軌最大豎向加速度約增大42%,心軌尖端最大豎向加速度增大約38%。連接軌和心軌尖端的最大豎向位移在250 km/h速度時,比200 km/h速度時增加 0.3%,基本軌的最大豎向位移隨著速度而變化,但變化較小。

圖5 道岔心軌尖端處輪下鋼軌豎向位移

表1 不同速度下道岔不同部位輪下鋼軌豎向加速度和豎向位移最大值

圖6 輪下鋼軌豎向加速度隨車輛通過速度的變化

圖7 輪下鋼軌豎向位移隨車輛通過速度的變化

2.2 幾何不平順對道岔轍叉區輪軌動力特性的影響

計算結果表明,車輛以200 km/h速度通過時,道岔轍叉區存在幾何不平順的情況下,車體在心軌尖端處產生豎向加速度和豎向位移的峰值;不考慮幾何不平順時,車體在同樣位置不產生豎向加速度和豎向位移的峰值,而且此時輪下鋼軌豎向位移要比有幾何不平順時的位移小50%,輪下鋼軌豎向加速度要減小84%(如圖8所示)。這說明幾何不平順是系統振動的激勵源之一。

圖8 車輛以200 km/h速度通過時道岔轍叉區輪下鋼軌豎向位移和豎向加速度比較

2.3 剛度不平順對道岔轍叉區輪軌動力特性的影響

文獻[3]采用改變連接軌軌下膠墊剛度,按照一定規律將道岔軌下剛度分布進行了優化,以達到改善道岔軌下剛度的均勻分布。模型參考該優化方案,分析了剛度平順性優化前后道岔轍叉區軌下剛度改變對輪軌動力特性的影響(詳見表2)。從表2可以看出,軌下剛度平順性優化前后,車輛的輪對、轉向架和車體的豎向加速度有所減小(車體約減小7%,轉向架約減小2%,輪對約減小1%)。這說明軌下剛度的合理設置,有助于減小車輛主要部件的振動,對車輛運行平順性的提高有一定的幫助。而對道岔的基本軌、連接軌和心軌尖端的豎向加速度有所減小(減小幅度在3%～5%左右)。由于平順性優化前后基本軌軌下剛度不變,基本軌除了磨耗產生的不平順外,沒有像心軌處那樣明顯的集中性不平順,故其最大豎位移不變;而平順性優化后的連接軌、心軌尖端處的軌下剛度減小,使最大位移略有增大。

表2 軌下剛度平順性優化前后車輛-軌道動力特性比較

2.4 道岔轍叉區動剛度分布規律

軌道豎向動剛度是指作用在鋼軌上某點的豎向激振力幅值與該點鋼軌豎向動位移幅值之比。它反映了某一瞬態受迫振動下的軌道剛度特性。本文是基于剛柔結合建模的多體系統,仿真中考慮了鋼軌的彈性特征,計算得出的動應變和動應力結果也為研究道岔轍叉區軌道動剛度分布規律提供了可能。

現按照動剛度的計算方法(即作用力幅值與動位移幅值之比),在考慮幾何不平順和剛度不平順的4種組合工況下,比較道岔轍叉軌道動剛度與靜剛度大小(如圖9所示)。

圖9 道岔轍叉在不同工況下軌道動剛度與靜剛度的比較

由圖9可見,在不同工況下動剛度是變化的,其變化幅度也會不同。道岔轍叉區的軌下剛度不平順嚴重,則軌道動剛度與靜剛度之比就有較大的偏差,因此軌道動剛度參數反映了軌道不平順對其有較大的影響。

3 結語

基于剛柔結合建模,建立了把道岔轍叉區軌道視為彈性體、車體視為剛性體的車輛-道岔耦合系統模型,分析在道岔轍叉區軌道幾何不平順及剛度不平順狀態下的輪軌系統動力特性。通過PATRAN與ADAMS軟件的聯合仿真,計算了道岔轍叉區在各種不平順條件下車體和軌道的動應變及動應力。結果表明,道岔轍叉區幾何不平順是車體振動的激勵源之一,軌下剛度分布是否均勻也直接關系到高速運行下列車的穩定性和旅客的舒適性。

通過對仿真結果的分析,發現將軌道視為彈性體比過去視為剛性體的計算結果偏小,但基本反映了在車輛通過道岔轍叉區時的輪軌振動規律;進而還分析了在4種工況下道岔轍叉區軌道動剛度的分布規律。可以看出,道岔轍叉區的靜剛度不平順分布對軌道瞬時動剛度也會產生較大的影響;道岔轍叉區軌道靜剛度不平順嚴重,則相應的軌道動剛度與靜剛度之比也有較大的差異。因此,在道岔軌下剛度平順化設計中,只考慮靜剛度是不夠的;動剛度分布規律為道岔轍叉區軌道剛度的優化提供了參考依據。

[1]Dietz S,Hippmann G,Schupp G.Interaction ofvehiclesand fiexible tracks by co-simulation of multibody vehicle sy stems and finite element track models[J].Vehicle Sy stem Dynamics Supplement,2003,37：372.

[2]Andersson C,Abrahamsson T.Simulation of interaction between a train in general motion and a track[J].Vehicle System Dynamics,2002,38(6)：433.

[3]Wallrapp O.Flexible bodies in multibody sy stem codes[J].Vehicle System Dy namics,1998,30(3)：237.

[4]金新燦,孫守光,陳光雄.車輛通過道岔時轉向架結構系統振動特性研究[J].工程力學,2007,24(1)：179.

[5]王平.道岔區輪軌系統動力學的研究[D].成都：西南交通大學博士學位論文,1997.

[6]譚曉春.道岔軌下剛度平順性與動態特性關系研究[D].上海：同濟大學碩士學位論文,2008.

[7]譚曉春,羅雁云.軌道交通列車過岔振動特征研究[J].城市軌道交通研究,2008(1)：28.

[8]朱劍月,顧福民,羅雁云.道岔尖軌軌下剛度改變對輪軌動力性能的影響[J].同濟大學學報,2002,30(2)：198.