基于均勻設計Goldstein-Price函數模擬研究

劉 寅,覃 紅

（華中師范大學數學與統計學學院,武漢替換為 430079）

基于均勻設計Goldstein-Price函數模擬研究

劉 寅,覃 紅＊

（華中師范大學數學與統計學學院,武漢替換為 430079）

Goldstein-Price函數是A.A.Goldstein和J.F.Price 1971年首次提出的.Goldstein-Price函數是一個比較經典的二元多項式函數模型.有許多作者從優化和算法的角度對它進行詳細的研究.最近,在計算機試驗設計中,一些作者對 Goldstein-Price函數進行模擬研究.本文利用均勻設計和中心化四次回歸的方法對 Goldstein-Price函數進行模擬,并重點考慮不同的均勻設計對擬合好壞的影響以及生成數據集時是否選取邊界點對擬合好壞的影響.

Goldstein-Price函數;中心化四次回歸方法;均勻設計

Goldstein-Price函數是一個二元八次多項式,它是A.A.Goldstein和J.F.Price[1]1971年中首次提出來的,其目的利用局部最小化算法去研究該二元多項式的局部最小值.最近,許多作者對Goldstein-Price函數從優化、算法、模擬等角度進行了研究.J.Andre等人[2]用改進的標準遺傳算法對 Goldstein-Price函數進行研究,P.Ranjan[3]從隨機超拉丁方設計出發利用序貫的方法對Goldstein-Price函數的等高區域進行了模擬.Chen[4]分別用帶有高斯相關函數的 Kriging模型、二次響應曲面多項式等六種方法以及均勻設計、正交設計等五種不同的設計方法對 Goldstein-Price函數進行擬合,并比較了不同設計擬合的效果.S.C.Chung和 Y.C.Hung[5]利用序貫權重均勻設計的方法對 Goldstein-Price函數的目標區域進行估計.

上述文獻都是利用計算機試驗來對Goldstein-Price函數這一經典的二元多項式函數模型進行研究.本文將利用均勻設計和中心化四次回歸的方法對 Goldstein-Price函數進行模擬,并分別考慮不同的均勻設計對擬合好壞的影響以及構造數據集時是否選取邊界點對擬合好壞的影響.

1 基本概念

1.1 均勻設計

均勻設計是由我國學者方開泰教授和王元教授于70年代末應復雜系統建立數學模型并研究其諸多影響因素的需要而提出的一種試驗設計方法[6-7],該設計要求試驗點均勻散布在試驗區域χ內.

由于均勻設計可以有效減少試驗次數和降低試驗成本,因此它被廣泛應用于許多領域來解決實際問題.現在越來越多的人對均勻設計的理論和應用感興趣,并取得了大量的理論和應用成果,詳細的情況可參見文獻[8-9].

一個n次試驗,s個因子,每個因子有q個水平的均勻設計通常記為Un（qs）.表1給了一個均勻設計U11（114）..這個設計有11次試驗,4個因子且每個因子有11個水平.這個設計參見文獻[10].下一節將利用 U11（114）去研究 Goldstein-Price函數.

表1 設計表Tab.1 Design table

1.2 Goldstein-Price函數

在 Goldstein-Price函數模型中,響應變量 y由下式決定

圖1 Goldstein-Price函數圖Fig.1 The picture of Goldstein-Price function

2 模擬研究

在 Goldstein-Price函數中,有2個輸出變量x1和 x2,因此用表1中給出的均勻設計U11（114）中的因子A和因子B本別來研究變量x1和x2.對每一個輸入變量,其11個水平1,2,…,11分別由原始模型的定義域[-2,2]中的11個等距的值來替換,這里不包括兩個邊界值.由此獲得的U11（112）設計和由公式（1）式得到的相應的輸出變量y值一并列入表2中.

現在考慮用多項式回歸模型的子模型來近似真正的模型（1）,為評價不同的輸入變量對 y的影響,分別作出 y對2個輸入變量之間按的關系圖,見圖2,其中圖（a）是固定 x2在其中間值即 x2=0得到,圖（b）是固定 x1在其中間值即 x1=0得到.這些圖表明傳統的中心化二次回歸模型已經不能很好的近似模擬真實模型,因此考慮用更高階的回歸模型來逼近真實模型.本文用 x的中心化四次回歸模型來近似逼近真實模型.

表2 設計表和相應的輸出變量 yTab.2 The design and related outputy

圖2 輸出變量對輸入變量的點圖Fig.2 Plots of y against input variables

現在基于表2來建立中心化四次回歸模型.由于在這個模型中有16個變量,用回歸分析中的模型選擇技術來去掉那些對模型沒有幫助的項,由于n<16,只有前進法和逐步回歸方法可以用.在這個問題中,借助于逐步回歸得到結果.對于逐步回歸方法,采用0.05作為顯著性水平去在模型中添加或刪除一個變量,表3給出了回歸模型（2）的方差分析（ANOVA）表,其中表3（a）給出了模型（2）的總體方差分析的結果,表3（b）給出了模型（2）各分項的分析結果,可以看出 y對兩個變量的中心化四次模型的逐步回歸結果,除常數項外,有9項進入回歸方程.

因此,得到如下的回歸模型

與其它模擬方法相比,本文采用的中心化四次回歸的方法具有較小的均方誤差,因此模擬的效果更好.結果可見表4.

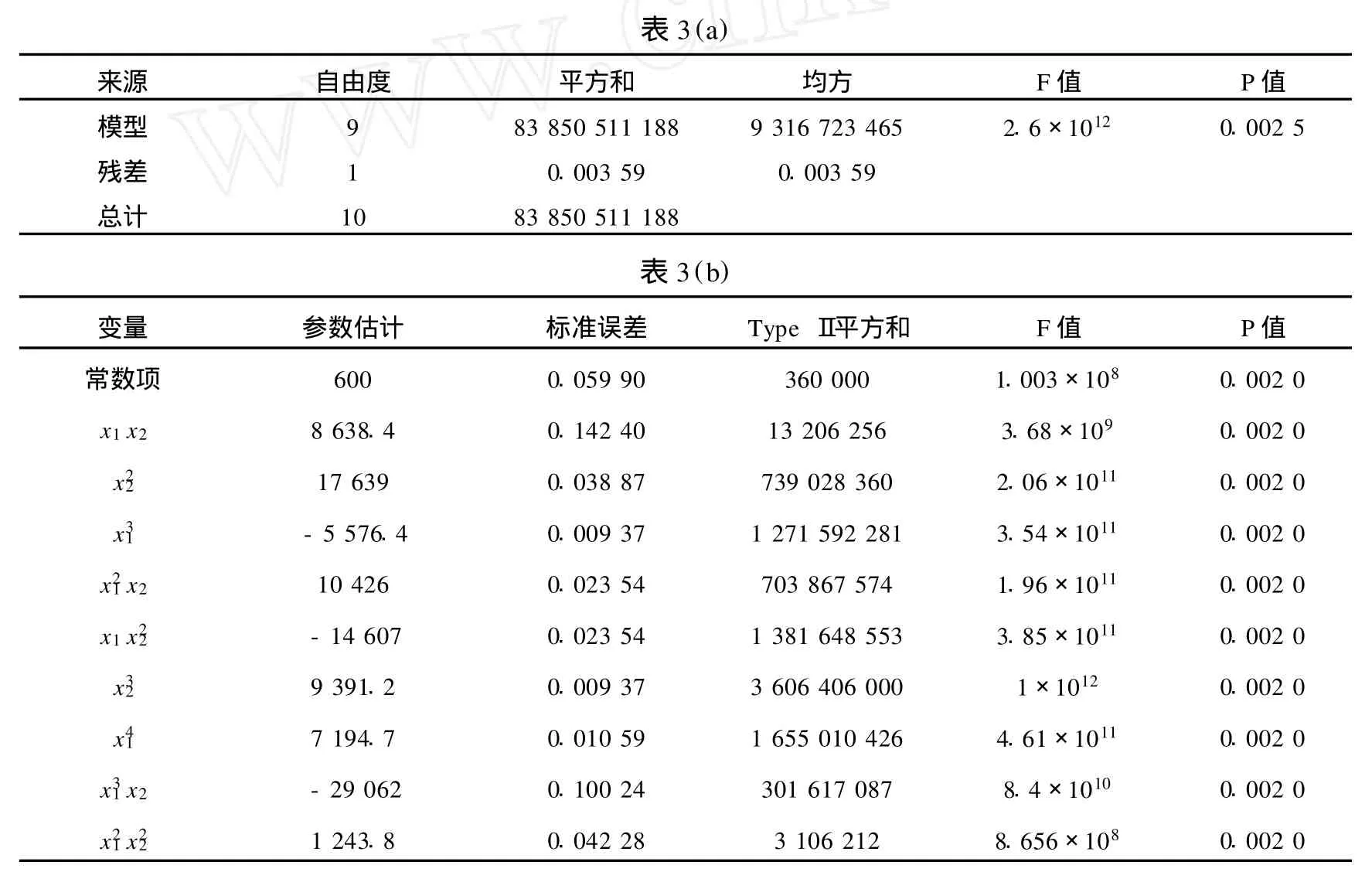
表3 模型（2）的ANOVA表Tab.3 ANOVA table for model（2）

表4 不同模擬方法比較[4]Tab.4 The comparison among different simulative methods

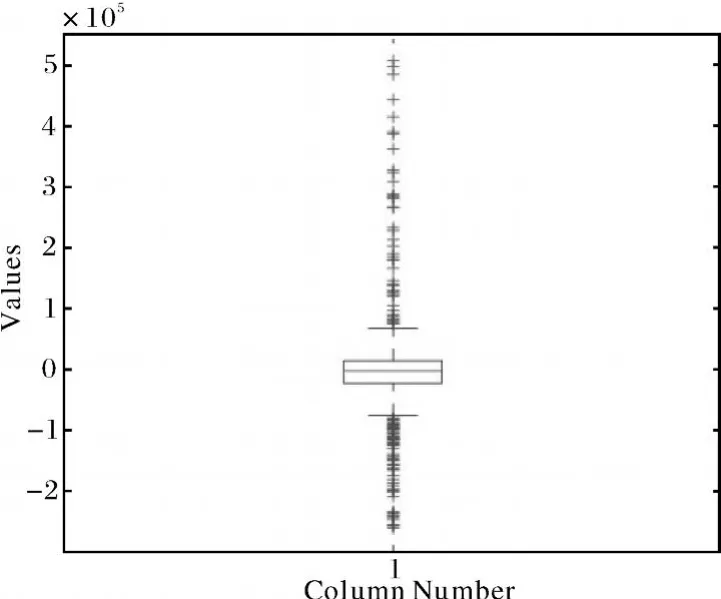
圖3 模型（2）在1 000個隨機點的預測誤差Fig.3 Prediction errors at

3 不同設計對回歸方程的影響

傳統的設計理論認為因子的水平數越高,由此擬合出來的回歸方程與真實模型應該越接近.下面,研究一下低水平與高水平的均勻設計對Goldstein-Price函數進行擬合的影響.這里以 R2作為衡量模型擬合好壞的標準.R2越接近于1,則擬合越好;反之,則擬合越差.

這里,分別考慮低水平 q=5,6,7和高水平 q=11,13,15時的均勻設計對 Goldstein-Price函數擬合的影響.選取均勻設計表來自于文獻[10],具體使用的設計見表5.

表5 不同水平的設計表Tab.5 Design tables with different levels

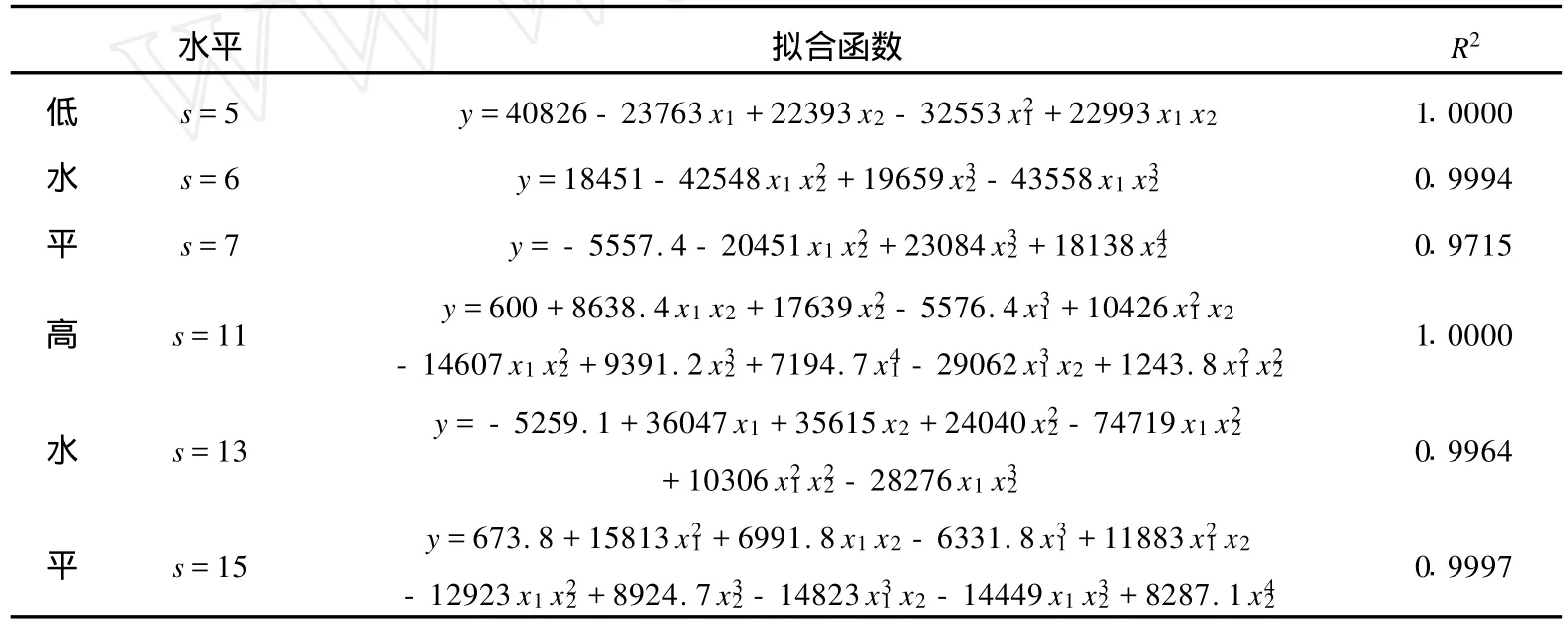
表6 高、低水平擬合函數的比較Tab.6 The comparison among simulative functions of high levels and low levels

根據表5來建立相應的數據集,并通過中心化四次回歸的方法對 Goldstein-Price函數進行擬合,得到表6.

這里以 R2low表示低水平時擬合函數的 R2,以R2high表示低水平時擬合函數的R2.從表中,可以很清楚的看到,在q=11,13,15時,均有 R2high>0.99,特別的 q=11時,有 R2high=1.0000;q=7時,R2low=0.9715<0.99,這說明因子的水平數越高,用中心化四次回歸的方法擬合的函數與真實模型越接近,也即用中心化四次回歸的方法擬合的方程和 Goldstein-Price函數非常接近.因此,可以認為在對Goldstein-Price函數進行中心化四次回歸建模時,通過高水平產生的數據集建立的擬合模型比低水平產生的數據集建立的擬合模型要好,這與傳統理論的結論是一致的.

4 是否取邊界對回歸方程的影響

在利用均勻設計表構造數據集時,通常有兩種方法,一種不取邊界值,另一種是取邊界值.下面來研究是否取邊界值對于中心化四次回歸建模的影響.

4.1 不取邊界的情形

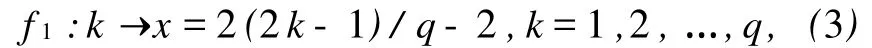
首先通過變換使得取值落在區間（-2,2）中,其中 k是因子的水平,q是因子的水平數.

以q=11為例來說明具體的方法.當不取邊界時,本文所用的均勻設計表為U11（112）.將通過變換（3）獲得的數據和由（1）式得到的相應的輸出變量 y值一并列入表7中.

基于表7中的數據,可以建立如下的回歸函數:

表7 q=11時設計表和相應的輸出變量 y（不取邊界）Tab 7 The design table and related outputyat levelq=11（without boundary）

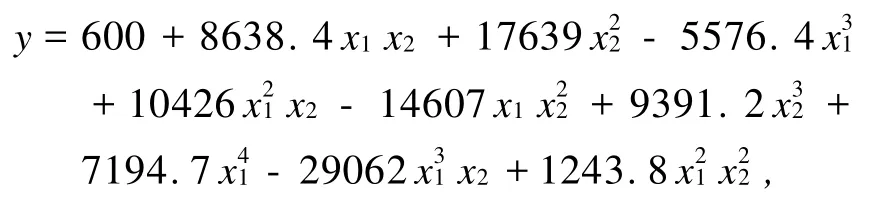
其中,R2=1.0000.

4.2 取邊界的情形

通過變換

k=1,2,…,q使得取值落在[-2,2]之間來構造數據集.

以q=11為例來說明具體的方法.當取邊界時,本文所用的均勻設計表為U11（112）.將通過變換（4）獲得的數據和由（1）式得到的相應的輸出變量 y值一并列入表8中.

表8 q=11時設計表和相應的輸出變量y（取邊界）Tab.8 The design table and related outputyat levelq=11（with boundary）

基于表8中的數據,可以建立如下的回歸函數:

其中,R2=0.9995.

4.3 比較

是否通過不取邊界值建立的數據集進行擬合的函數要比通過取邊界值建立的數據集進行擬合的函數要好呢?下面按照5.1和5.2中介紹的方法對q=13和q=15的情形進行模擬研究,具體結果列舉在表9中.

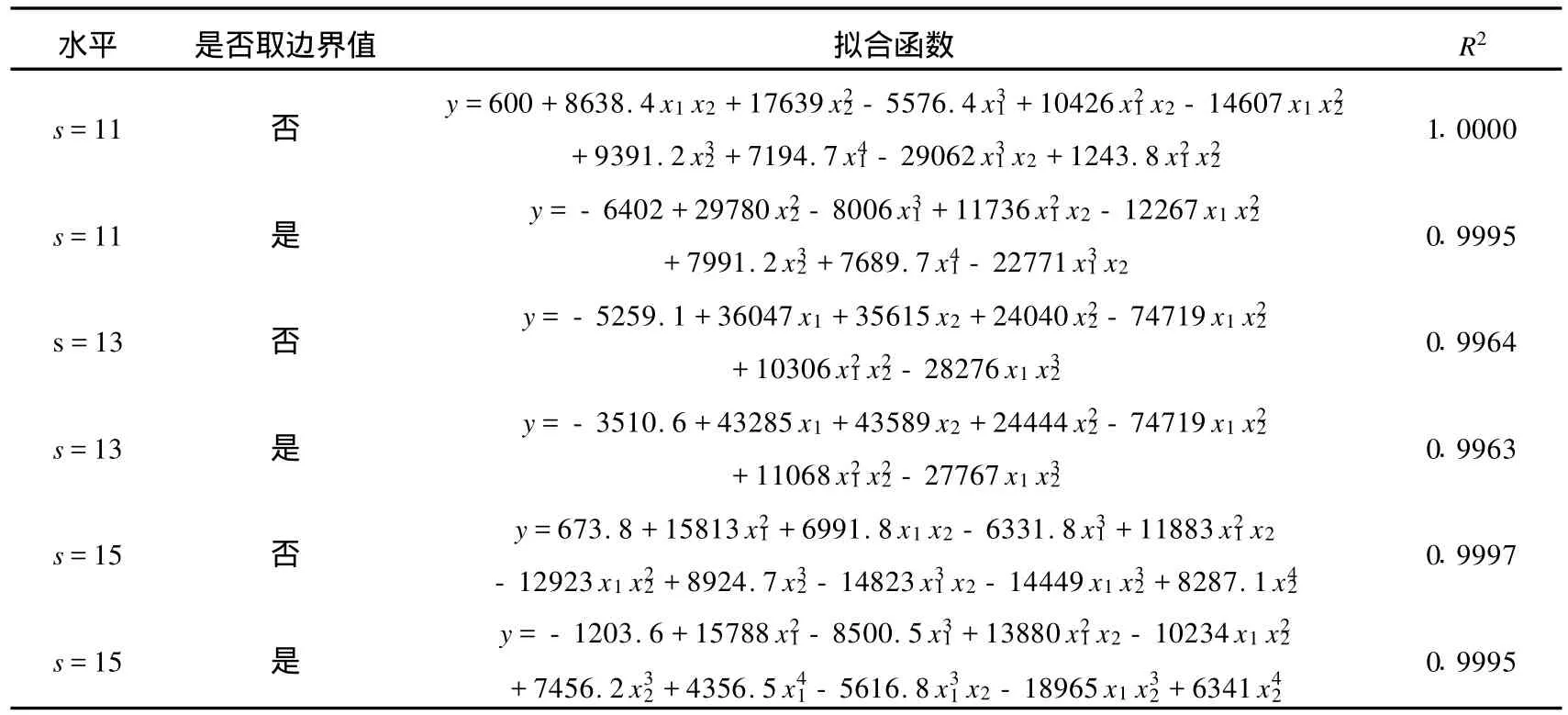
表9 取邊界與不取邊界擬合函數的比較Tab.9 The comparison among smulative functions of choosing points with boundary and without boundary

以 R2wo表示不取邊界值時擬合函數的 R2,以R2w表示取邊界值時擬合函數的R2.從表9中,可以看到當 q分別取11、13、15時,均有 R2wo>R2w成立,也就是說通過不取邊界值進行擬合得到的函數比通過取邊界值進行擬合得到的函數要好,也即通過不取邊界值進行擬合得到的函數與真實模型更接近.

這一點,也可以借助于 Goldstein-Price函數的函數圖像加以解釋.從圖1中看到 Goldstein-Price函數的局部極值點主要集中在函數圖像的邊界位置處,因此,當數據集不取到邊界點時,得到的擬合函數更接近于真實模型.

5 結束語

本文作者利用中心化四次回歸的方法對Goldstein-Price函數進行模擬,分別考慮不同的均勻設計對擬合好壞的影響以及構造數據集時是否選取邊界點對擬合好壞的影響.首先,本文中的數據是基于一類重要的空間填充設計——均勻設計——生成的,而均勻設計具有較好的穩健性,它能夠將試驗點均勻的散布在試驗區域內,從而有助于建模,使得近似模型能和真實模型在全試驗區域內都很接近[6].其次,本文重點考慮了取邊界值與不取邊界值對擬合好壞的影響,這一點在過去的文獻中是沒有的.同時,這個例子也說明對于 Goldstein-Price函數,用高水平對函數進行擬合比低水平要好,不取邊界值時擬合的函數要優于取邊界值時擬合的函數.

[1]Goldstein A A,Price J F.On descent from local minima[J].Mathematics of Computation,1971,25:569-574.

[2]Andre J,Siarry P,Dognon T.An improvement of the standard genetic algorithm fighting premature convergence[J].Advances in Engineering Software,2001,32（1）:49-60.

[3]Ranjan P,Binggham D,Michalidis G.Sequential experiment design for contour estimation from complex computer codes[J].Technometrics,2008,50（4）:527-541.

[4]Victoria C,Chen P.A review on design,modeling and applications of computer experiments[J].IIE Transactions,2006,38:273-291.

[5]Chung S C,Hung Y C.Uniform design over general input domains with applications to target region estimation in computer experiments[J].Computational Statistics&Data A-nalysis,2010,54:219-232.

[6]方開泰.均勻設計[J].應用數學學報,1980,3:363-372.

[7]王 元,方開泰.關于均勻設計與試驗設計（數論方法）[J].科學通報.1981,26:65-70.

[8]Fang K T,Wang Y.Number-Theoretic Methods in Statistics[M].London:Chapman and Hall,1994.

[9]Fang K T,Li R,Sudjianto A.Design and modeling for computer experiments[M].London:Chapman and Hall,2005.

[10]方開泰.均勻設計與均勻設計表[M].北京:科學出版社,1994.

Abstract:Goldstein-Price function was first proposed by A.A.Goldstein and J.F.Price in 1971,which is a classical polynomial model with two variables.Considerable study has been done on this function in computer experiments.In this article,the quadratics regression method is used to simulate the Goldstein-Price function,and we consider the influence on the simulative the Goldstein-Price function,and we consider the influence on the simulative functions resulted from choosing different uniform designs as well as whether choosing boundary points to construct data or not.

Key words:Goldstein-Price function;quartics regression method;uniform design

Goldstein-Price function in the application of uniform designs

LIU Yin,QIN Hong
（School of Mathematics and Statistics,Huazhong Normal University,Wuhan 430079）

O212.6

A

1000-1190（2010）04-0535-06

2010-04-23.

國家自然科學基金項目（10671080）;教育部新世紀優秀人才支持計劃項目（06-672）.

＊通訊聯系人.E-mail:qinhong@mail.ccnu.edu.cn.