分塊矩陣在矩陣證明題中的應用
趙中華
南京財經大學應用數學學院 南京 210046
分塊矩陣在矩陣證明題中的應用
趙中華
南京財經大學應用數學學院 南京 210046
結合矩陣中的一些結論,討論分塊矩陣在矩陣證明題中的應用。例題說明分塊的方法是矩陣證明題中較簡捷、有效的方法。
分塊矩陣;秩;初等變換
Author’s address Institute of Applied Maths, Nanjing Univ. of Finance & Economics, Nanjing, China 210046
在高等代數中,矩陣分塊的方法對矩陣證明題來說是一種很好的方法。本文結合矩陣的初等變換、矩陣秩的有關性質,對相關矩陣進行分塊或構造相關的分塊矩陣,討論分塊矩陣在證明題型中的應用。
先以常用的2×2的分塊矩陣為例,給出幾個與分塊矩陣相關的定義與性質。
由定義1可得,分塊初等矩陣具有以下形式:
其中P、Q分別是m階和n階可逆方陣。
注:在使用分塊初等矩陣乘法時,要注意所作分塊必須使得分塊乘法的運算能進行。
由定義1,給出分塊初等矩陣的性質。
性質1:對分塊矩陣進行一次行(列)初等變換,相當于左(右)乘一個相應的分塊初等矩陣。
性質2:分塊初等矩陣是可逆矩陣,分塊初等變換不改變矩陣的秩。
性質3:對一個分塊矩陣左(右)乘一個分塊初等矩陣,不改變原分塊矩陣的秩。
1 分塊矩陣在秩的證明題中的應用
證明方法:利用分塊初等矩陣的性質和秩的性質。秩的2個性質:

1.1 在秩的不等式證明中的應用
例11 設 A=As×n, B=Bn×m。
證明:r( A) +r( B ) ?n ≤r( A B ) ≤ min{r( A), r( B)}。

故r( A B ) ≤r( C ) =r( A)。
注:本例中,若AB=0, 則r ( A)+ r(B)≤n。
1.2 在秩的等式證明中的應用
例22 A設為n階方陣,證明:
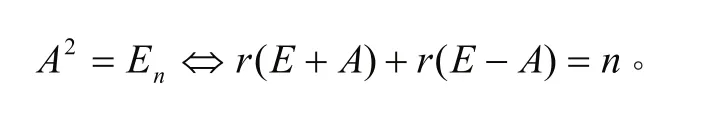

即:r(E+A)+r(E?A)=r(E?A2)+r (E)=r(E?A2)+n
∴r(E+A)+r (E?A)=n?A2=E
2 分塊矩陣在矩陣存在性問題中的應用
證明方法:利用矩陣秩的化簡結論。

例33 設 B = Bm×n,且 r( B )=n。
證明:存在 A = An×m,且 r( A )=n,使 ABB = En。


3 分塊矩陣在矩陣分解中的應用
證明方法:利用矩陣秩的化簡結論。
例44 證明:任一方陣A都可寫為A=BC,其B2=B,C可逆。
證明 設 rAr =)( ,則存在n階可逆矩陣P,Q,使

例5(滿秩分解) 證明:對任意m×n階矩陣A,設 r( A )=r,則有A=H L,其中 H=Hm×r, L=Lr×n,且r(H)= r (L)=r 。

4 分塊矩陣在矩陣行列式相關問題中的應用
證明方法:利用分塊矩陣的初等變換及行列式的運算。
例66 設 A=Am×n,B=Bn×m,m≥n。


注:此題也可轉化為證明秩的問題r(λEm?AABB)=m ?n+r (En?BBAA)。
5 分塊矩陣在矩陣求逆問題中的應用
證明方法:利用分塊矩陣的初等變換及分塊矩陣求逆的方法及結論。


所以,由分塊矩陣的逆,可得:

在高等代數中,利用分塊的方法證明矩陣問題的題目還有很多,這里只是列舉了其中的一些加以討論。并且,有的例題也有其他的證明方法,這里不再一一給出。另外,分塊的方法與齊次線性方程組解的結構相結合(一般是系數矩陣的列分塊),也可以解決一些問題。例如,“若AB就可以用齊次方程組解的結構來證明。總之,由以上例子可以看出,矩陣分塊在矩陣證明題中是一種較簡捷、有效的方法。
[1]李守金,郭秀剛,牟樹杰.分塊矩陣的初等變換在行列式中的應用[J].中國教育技術裝備,2009(11):91-94
[2]雷英果.分塊矩陣及其應用[J].工科數學,1998,14(4):150-154
[3]王品超.高等代數新方法[M]].濟南:山東教育出版社,1989
Application of Block Matrix in Proof of Matrix
//Zhao Zhonghua
The paper discusses the application of block matrix in the proof of matrix, combined with the conclusions of matrix. Examples show that the way of block is more effective and succinct in the proof of matrix.
block matrix; rank; primary transformation
O241.6
B
1671-489X(2010)09-0052-03
10.3969 /j.issn.1671-489X.2010.09.052
作者:碩士,講師。

