Gouy-Chapman雙電層模型在蒙脫石長程膨脹中應用

賈 景 超, 楊 慶＊,2

(1.大連理工大學土木工程學院巖土工程研究所,遼寧大連 116024;2.大連理工大學海岸和近海工程國家重點實驗室,遼寧大連 116024)

0 引 言

膨脹土因為含有膨脹性礦物——蒙脫石而具有吸水膨脹特性[1].蒙脫石顆粒由相互平行的晶層疊加而成,而蒙脫石的膨脹正是源于晶層之間的吸水膨脹.晶層之間的膨脹通常分為兩個階段:第一階段的膨脹稱為晶格膨脹或水合膨脹;第二階段的膨脹稱為滲透膨脹[1、2].Zhang等[3]排除膨脹機理的影響將這兩個階段分別稱為短程膨脹和長程膨脹.雖然晶層之間的膨脹大體上分為兩個階段,但是這兩個階段沒有明顯的分界點.奧爾芬[1]認為第一階段的水合膨脹大約為1 nm(相當于4個水分子層),晶層間距超過1 nm之后,水合力就不重要了;而Israelachvili等[4]認為水合階段大概相當于10個水分子層,晶層間距大約為2.5 nm.另外由于晶格膨脹涉及晶層表面的水合和晶層間離子的水合,哪種因素占支配地位至今仍未搞清楚[1、4、5].第二階段的滲透膨脹歸根結底是由同晶置換作用而導致的蒙脫石晶層內部電荷不平衡,這種不平衡表現為晶層表面帶負電.為了中和這些負電荷,陽離子被吸附到晶層表面,蒙脫石吸水之后被吸附的陽離子擴散到水中,這些陽離子一方面受晶層表面負電荷的靜電作用,一方面由于布朗運動而產生遠離表面的擴散趨勢,從而使得水中的陽離子和晶層表面的陰離子形成擴散雙電層,擴散到水中的陽離子云稱為擴散層,描述擴散層離子分布的模型中Gouy-Chapman雙電層模型是較簡單且得到廣泛應用的一種[1、6、7].相互平行晶層之間的雙電層相互重疊會產生雙電層斥力,而眾多學者已證明雙電層斥力等于平行晶層的中平面處離子的滲透壓和晶層外平衡溶液中相對應離子滲透壓之差[8～10],從而可以結合滲透壓理論和Gouy-Chapman相互作用雙電層模型建立晶層間膨脹壓力模型[1、8],以下簡稱Gouy-Chapman雙電層模型.

蒙脫石晶層間的膨脹得以實現的另一個重要原因是晶層之間的聯結力主要是范德華引力,這種作用力較弱,從而使得水合力和雙電層斥力能夠克服它而產生膨脹壓力[1].

長期以來對于第二階段的滲透膨脹或者長程膨脹的機理存在爭議:一種觀點認為長程膨脹源于晶層間的雙電層斥力,并通過與精確的試驗結果比較認為長程膨脹符合雙電層理論,可以用Gouy-Chapman模型或其改進模型來描述[4、11～15];另一種觀點則認為晶層間水分子的結構性排列是產生長程膨脹的決定性因素,雙電層理論不能解釋這種現象[3、16、17].

為澄清上述爭議,本文基于Zhang等[3]的試驗數據對Gouy-Chapman模型從膨脹壓力-晶層間距關系以及晶層間距-電解質濃度關系兩個方面對模型進行驗證,并對簡化Gouy-Chapman模型的適用性進行分析.

1 Gouy-Chapman模型的驗證

1.1 對膨脹壓力-晶層間距關系的驗證

Gouy-Chapman模型包括以下幾個方程[1 、6 、8 、18]:

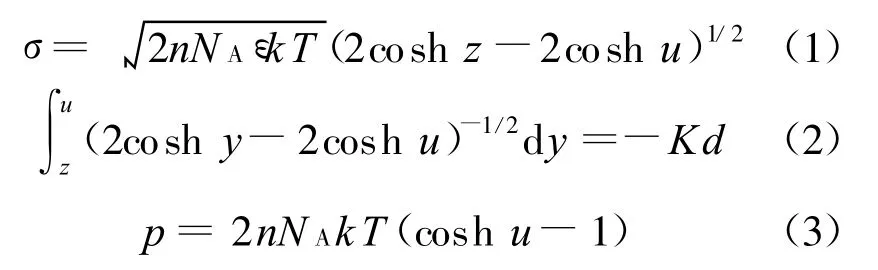
式中

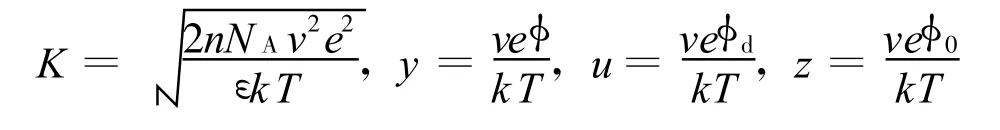
d為兩平行晶層間距的一半;σ為晶層表面電荷密度(C/m2),本文σ值和Zhang等的取值都取自文獻[19],為0.108;ε為電容率,等于相對電容率 εr(=80)和真空電容率ε0(=8.854×10-12C2/(N·m2))之積;k為 Boltzmann常數,1.38×10-23J/K;T為熱力學溫度,本文取298 K;v為離子化合價;e為單位電荷電量,1.602×10-19C;n為晶層外平衡電解質溶液物質的量濃度(mol/L);NA為阿伏伽德羅常數(1/mol);p為滲透壓力或雙電層斥力(kPa); 為擴散雙電層中任意一處的電勢; 0和 d分別為晶層表面和平行晶層中間處的電勢;y、z、u分別為 、 0、 d對應的量綱一量.

在σ和n已知的情況下由晶層間距λ=2d計算滲透壓力,需要知道u的值,但是由于式(2)是橢圓積分,很難將3個方程合并為1個方程從而直接由d求得p.Sridharan等[18]建議通過擬合方程中的u和Kd得到擬合關系式,再將擬合式代入式(3)得到p關于d的函數.詳細過程如下:假設一系列p,可以由式(3)得到一系列u,已知σ和u可以由式(1)得到z,再通過精確的數值積分可以得到與u對應的Kd,最后將u和Kd擬合即可得擬合關系式,其形式一般為

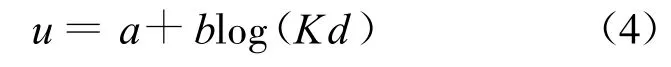
其中常數a和b僅受σ和n的影響.用這種方法得到的擬合式相關系數一般可達0.99.再將式(4)代入式(3)即可得Gouy-Chapman模型的擬合形式:

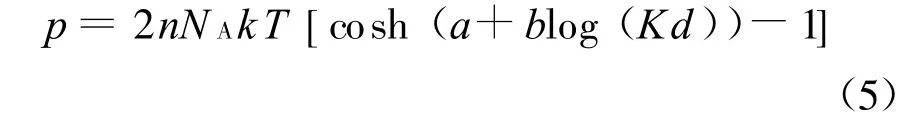
Zhang等的試驗中所加的膨脹壓力π實際等于雙電層斥力和范德華力之差,范德華力的表達式為[15]

式中:A=2.2×10-20J,為 Hamaker常數;t為晶層的厚度,一般取0.93 nm.從而有

用上式對Zhang等的試驗數據進行擬合,結果如圖1所示.從圖1可以看出,當晶層外的平衡電解質濃度n≤0.01 mol/L時,式(7)能較好地擬合試驗數據,但是在n為0.1和0.3 mol/L兩種情況下,當膨脹壓力大于200 kPa時,理論值和試驗值產生偏差.原因可能在于當平衡電解質濃度較大時,晶層間離子濃度也隨之增大,隨著晶層間距的減小,離子水合產生的水合力影響逐漸顯現,使得僅僅用雙電層理論計算的理論結果小于試驗結果.

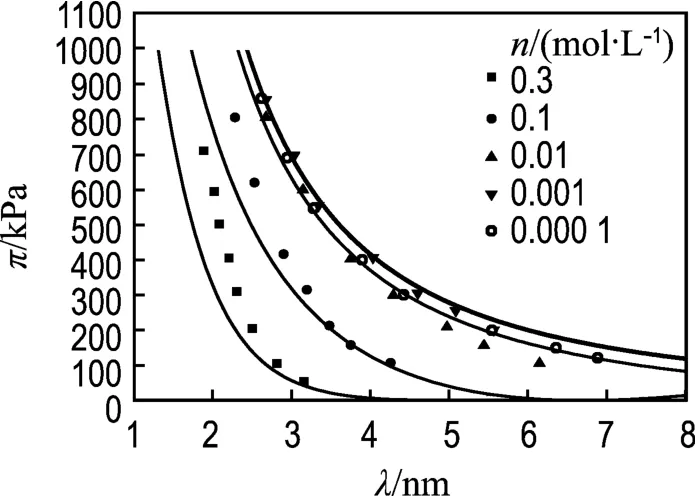
圖 1 π-λ的試驗點及 Gouy-Chapman模型擬合曲線Fig.1 Experimental points for π-λ together with the predicted curves calculated by the Gouy-Chapman model

用同樣的計算方法,對文獻[14]的試驗數據擬合結果如圖2所示.試驗用Hectorite土的表面電荷密度σ大約為 0.001 C/m2,電解質濃度為10-5mol/L.需要注意的是,文獻[14]中晶層間的作用是從能量的角度表示的,本文中轉化為壓強形式.

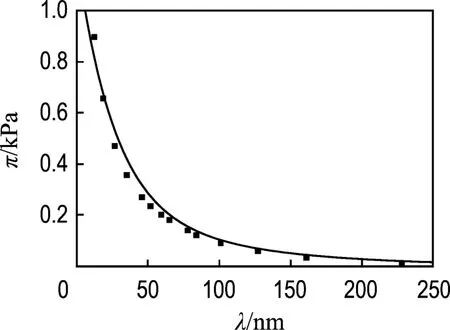
圖2 對文獻[14]試驗數據的擬合結果Fig.2 Fitting results on the experimental data of Lit.[14]

Quirk等[15]從另外一個角度用Gouy-Chapman模型對Zhang的數據進行擬合,式(2)用一個橢圓函數來表示.計算過程如下:已知膨脹壓力和與之對應的晶層間距的試驗值πexp和λexp,可以由λexp通過式(6)得 pv,進而由式(7)求得雙電層斥力p,然后由式(3)得 u,已知σ,則z可通過式(1)求得,u和z都已知后通過數值方法解橢圓函數即可得Kd,最后可求得晶層間距理論值λth.計算結果如圖3所示.

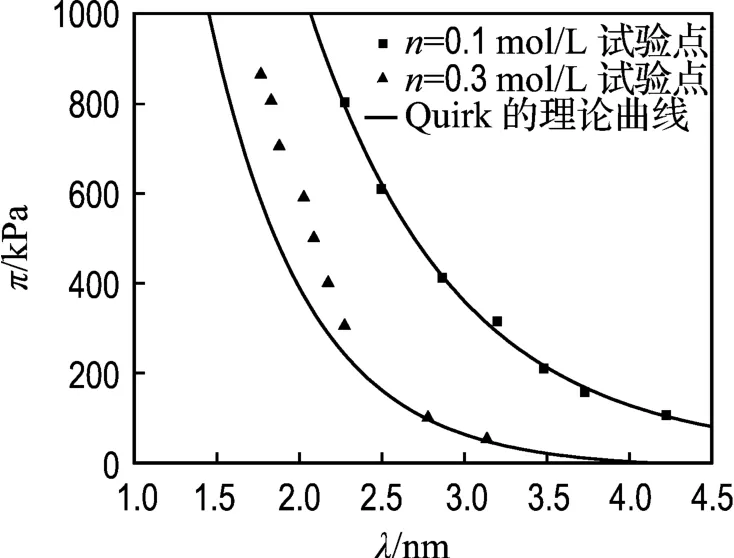
圖3 π-λ的試驗點以及Quirk的理論曲線Fig.3 Experimental points for π-λtogether with the theoretical curves presented by Quirk

從圖 3可知,當 n=0.1 mol/L時,采用Quirk的方法計算結果和試驗數據能夠吻合,但是當n=0.3 mol/L時,擬合效果同樣不理想.因為Quirk采用的方法是逆推法,前提是λ和π的試驗值都已知,才能推得 λth,當用 λexp求得 pv,并由式(7)求得p的同時,也將可能存在的水合力轉移到雙電層斥力p上,才使得λth能與試驗值基本吻合.然而當n=0.3 mol/L時擬合的結果不準確說明這種逆推法當存在水合力時可能存在偶然性.而且,這種方法只能用來驗證雙電層的適用性,并不能由晶層間距預測膨脹壓力.

用式(7)對Viani等[17]的一組試驗數據擬合結果如圖4所示,Viani的這組試驗用土與Zhang的試驗用土都是Upton蒙脫石,而且用的試驗儀器一樣,但試驗結果卻有偏差.Zhang對此的解釋是:雖然兩人都是用X光衍射法測得晶層間距λ,然而處理數據的方法不同導致了試驗結果的偏離.Zhang建議將Viani的試驗點向右平移0.25 nm兩種試驗結果就會一致,即如果采用Zhang的方法處理數據,Viani的試驗結果也基本符合雙電層理論.

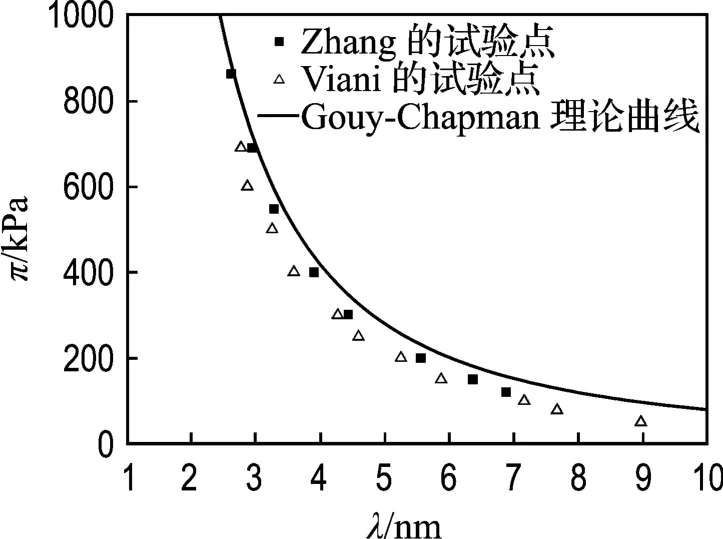
圖4 n=0.0001 mol/L時,Zhang和 Viani的 π-λ試驗點以及Gouy-Chapman模型理論曲線Fig.4 Relation between πand λat 0.0001 mol/L obtained by Zhang and Vianiand the theoretical curve of Gouy-Chapman model

1.2 對晶層間距-電解質濃度關系的驗證

Zhang等不贊成雙電層理論的另一個理由是當膨脹壓力π為定值時,晶層間距λ隨平衡電解質濃度n變化的試驗結果與用Gouy-Chapman模型計算得到的理論值不一致.本文接下來的驗證將說明平衡電解質濃度對晶層間距的影響基本符合雙電層理論.

n 分別取 0.1、0.01 、0.001、0.0001 mol/L,將膨脹壓力試驗值πexp代入式(7),從而求得理論晶層間距λth,將πexp對應的晶層間距理論值和試驗值對比如圖5所示.n沒有取0.3 mol/L是考慮到此時的水合力影響較大.π之所以取200、300、400 kPa,是因為此3種情況下都有試驗數據.

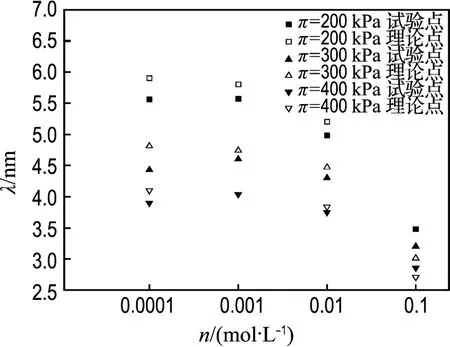
圖5 不同 π值晶層間距λ隨電解質濃度n變化的試驗點與理論結果的比較Fig.5 Comparisons of the observed points of λvs.n with the theoretical values at different designated values of π

從圖5可以看到,Gouy-Chapman模型的理論值和試驗值基本一致或接近.說明當膨脹壓力不變,0.0001 mol/L≤n≤0.1 mol/L時,晶層間距隨電解質濃度的變化基本符合Gouy-Chapman雙電層模型.

1.3 簡化的Gouy-Chapman模型

奧爾芬[1]曾指出,當間距為 2d的平行晶層間的雙電層相互作用較弱時(Kd>1),可以將平行晶層中平面處的電勢等價于兩個獨立的雙電層在離表面距離為d處的電勢之和,即[1]

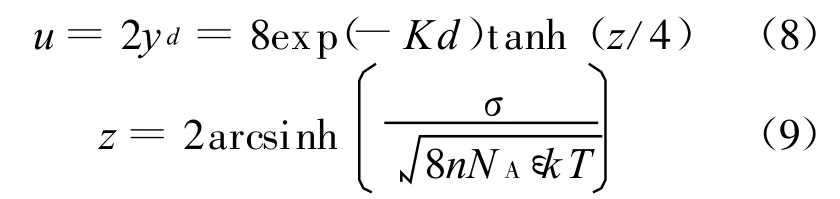
式中z為獨立晶層表面量綱一電勢.由于雙電層相互作用較弱時u較小,式(3)可借助泰勒級數簡化為

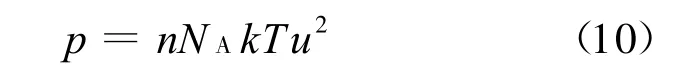
將式(8)、(9)代入式(10)即可得簡化的Gouy-Chapman模型:

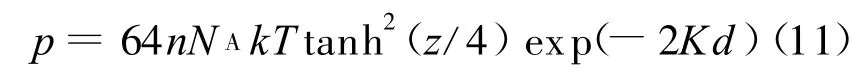
對于Gouy-Chapman雙電層模型,σ=0.108 C/m2,n=0.01、0.001 mol/L時,K 分別為0.325、0.1027 nm-1,根據1.1介紹的方法可得u-Kd擬合式分別為

其相關系數R2=0.9999,所以可以用上式代替u、Kd的數值解代入式(3)與式(11)進行比較,結果如圖6所示.

從圖中可以看出,Kd<1時兩種曲線有偏差,尤其當Kd<0.75以后;而Kd>1時,兩種曲線幾乎重合,此時可以用簡化的模型代替Gouy-Chapman模型.雖然簡化 Gouy-Chapman模型不用求解橢圓積分,較Gouy-Chapman模型簡單,但是這里僅僅給出了兩種情況,并不能說明所有情況下Kd>1時簡化模型都能適用,而Gouy-Chapman模型的擬合形式并不受Kd的影響,因此采用Gouy-Chapman模型還是簡化模型的擬合形式需要根據具體問題來選擇.

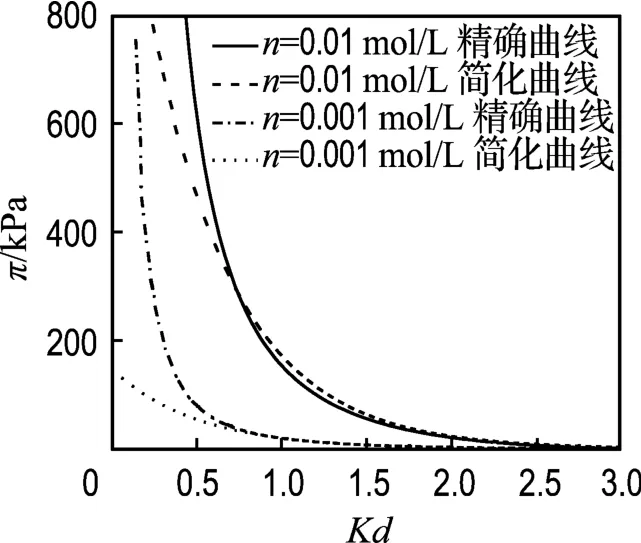
圖6 Gouy-Chapman模型曲線與簡化Gouy-Chapman模型曲線的比較Fig.6 Comparisons of the Gouy-Chapman model curves with the simplified Gouy-Chapman model curves

2 討 論

(1)Zhang等[3]所做的試驗僅僅是為了研究晶層間或相互平行的顆粒間的作用力,所以本文討論的Gouy-Chapman模型僅限于模擬平行晶層或平行顆粒間的長程相互作用,并不能直接應用于具有宏觀尺寸的土體試樣,即不能將平行晶層或平行顆粒間的膨脹壓力等同于膨脹土宏觀試樣的膨脹壓力,因為宏觀試樣中顆粒的取向隨機分布,這樣一方面會導致顆粒間呈邊-面結合,因此產生的靜電力以及顆粒間的相互作用會影響單個顆粒內部或顆粒間產生的膨脹壓力在宏觀試樣上的顯現,另一方面,平行晶層或平行顆粒間產生的膨脹壓力不會只在試樣的一個方向顯現,豎向的膨脹壓力并不等于總膨脹壓力.如何將細觀的膨脹壓力平均至宏觀尺度將是下一步的努力方向.

(2)直接量測晶層間作用力和晶層間距的方法主要有Zhang等[3]所用的傳統方法,這種方法是通過氮氣對試樣加壓的同時用X光衍射儀對晶層間距進行觀測.較為精確的儀器有Israelachvili[11]研制的表面測力儀(SFA)以及原子力顯微鏡(AFM).Liang等[20]對兩種儀器進行了對比.本文中Nishmura等[14]的試驗數據即為AFM所測結果.

(3)圖1中,n≤0.01 mol/L的情況下,當膨脹壓力小于200 kPa時,Gouy-Chapman模型的預測結果與試驗數據稍有偏差,這可能是由電荷規則(charge regulation)效應引起的.Chan等[21]用考慮電荷規則效應的Gouy-Chapman-Stern-Grahame模型對雙電層相互作用力進行了解釋,在低壓力時擬合效果較好,但是在高壓力下,結果并不理想.

3 結 論

(1)當n≤0.01 mol/L時,Gouy-Chapman模型能夠較好地模擬膨脹壓力π和晶層間距λ之間的關系;當n為0.1和0.3 mol/L時,由于受晶層間水合力的影響,π-λ關系部分服從 Gouy-Chapman模型.

(2)當膨脹壓力為定值,0.0001 mol/L≤n≤0.1 mol/L時,晶層間距隨電解質濃度的變化與Gouy-Chapman模型的預測結果基本一致.

以上兩方面的驗證,說明在沒有水合力的影響下蒙脫石晶層間的長程膨脹符合雙電層理論,從而可以用Gouy-Chapman模型定量地模擬.

[1]范·奧爾芬.粘土膠體化學導論[M].許冀泉,等譯.北京:農業出版社,1982

[2]NORRISH K.The swelling of montmorillonite[J].Discussions of the Faraday Society,1954,18(1):120-134

[3]ZHANG F S,LOW P F,ROTH C B.Effects of monovalent,exchangeable cations and electrolytes on the relation between swelling pressure and interlayer distance in montmorillonite[J].Journal of Colloid and Interface Science,1995,173(1):34-41

[4]ISRAELACHVILI J N,MCGUIGGAN P M.Forces between surfaces in liquids[J].Science, 1988,241(4867):795-780

[5]ISRAELACHVILI J N,WENNERSTROM H.Role of hydration and water structure in biological and colloidal interactions[J].Nature,1996,379(6562):219-225

[6]M ITCHELLJ K.Fundamentals ofSoil Behavior[M].New York:John Wiley&Sons,1976

[7]BRADY N C,WEIL R R.The Nature and Properties of Soils[M].New Jersey:Prentice Hall,1996

[8]VERWEY E J W,OVERBEEK J.Theory of the Stability of Lyophobic Colloids[M].Amsterdam:Elsevier,1948

[9]HIEMENZ P Z.膠體化學原理[M].周祖康,等譯.北京:北京大學出版社,1986

[10]HUNTER R J.Foundations of Colloid Science:Vol.1[M].Oxford:Clarendon Press,1986

[11]ISRAELACHVILI J N.Intermolecular and Surface Forces[M].London:Academic Press,1985

[12]PASHLEY R M.DLVO and hydrationforces between mica surfaces in Li+,Na+,K+,and Cs+electrolyte solutions:A correlation of double-layer and hydration forces with surface cation exchange properties[J].Journal ofColloid and Interface Science,1981,83(2):531-546

[13]DUCKER W A,SENDEN T J,PARSHLEY R M.Direct measurement of colloidal forces using an atomic force microscope [J].Nature, 1991,353(6341):239-241

[14]NISHMURA S,KODAMA M,YAO K,et al.Directsurface force measurementforsynthetic smectites using the atomic force microscope[J].Langmuir,2002,18(12):4681-4688

[15]QUIRK JP,M ARCELJA S.Application of double-layer theories totheextensive crystalline swelling of Li-montmorillonite[J].Langmuir,1997,13(23):6241-6248

[16]LOW P F.Structural component of the swelling pressure of clays[J].Langmuir,1987,3(1):18-25

[17]VIANIB E,LOW P F,ROTH C B.Direct measurement of the relation between interlayer force and interlayer distance in the swelling of montmorillonite[J].Journal of Colloid and Interface Science,1983,96(1):229-244

[18]SRIDHARAN A,CHOUDHURY D.Swelling pressure of sodium montmorillonites [J].Geotechnique,2002,52(6):459-462

[19]LOW P F. The swelling of clay:Ⅱ.Montmorillonites[J].Soil Science Society of America Journal,1980,44(4):667-676

[20]LIANG Y C,HILAL N,LANGSYON P,et al.Interaction forcesbetween colloidalparticlesin liquid:Theoryand experiment[J].Advances in Colloid and Interface Science,2007, 134-135:151-166

[21]CHAN D Y C,HEALY T W,SUPASITI T,et al.Electrical double layer interations between dissimilar oxide surfaces with charge regulation and Stern-Grahame layers[J].Journal of Colloid and Interface Science,2006,296(1):150-158