MPI下單源點最短路徑的并行算法設計與分析

黎 源，王會進

(暨南大學 信息科學技術學院，廣東 廣州510632)

隨著高性能技術的發展，并行處理在解決人類重大挑戰問題方面發揮著越來越重要的作用。并行計算從傳統的超級計算機平臺，轉移到一組高性能節點或工作站/PC機構成的稱之為集群的計算平臺上，機群成為并行計算平臺的一個趨勢。并行程序設計是并行處理的核心技術。MPI(Message Passing Interface)即消息傳遞接口，是一個由眾多并行計算機廠商、軟件開發單位/組織、并行應用單位等共同維護的標準，是目前最流行的分布存儲并行編程環境。本文基于MPI進行并行程序設計的研究工作。

1 研究背景

平面中帶權圖中的最短路徑問題是計算機科學中一個被廣泛研究的對象，目前出現了大量并行求解最短路徑問題的算法。Chandy和Misra提出了一種計算k個最短路徑問題的并行算法，該計算將所有頂點到給定頂點的k個最短路徑之間的復雜度表示為O(m+nlog2n+nk)[1]。已知的最好的算法是Cohen[2]提出的運行在EREW PRAM上的算法，該算法在空間復雜度為O(n3/2)時的時間復雜度為O((log2n)4)。Traff[3]等人基于前綴計算、列表分級、排序等方法實現了Dijkstra串行算法的并行版本。Adamson、Tick[4]和 Traff[5]使用一個分布的共享存儲器使標簽設定算法并行化。由于同一時刻只是具有最短距離標簽的節點才能從隊列中取出，因此實驗中觀察到標簽設定算法具有弱并行性。Traff通過允許處理器取出多于一個的節點來改善性能。Romeijn和Smith[6]通過在分布式網絡中求解近似最短路徑樹來嘗試減少標簽設定算法的通信要求。Bertsekas等人[7]對幾個并行標簽算法在有8個處理器的共享存儲機器上作了實驗比較，結果發現有一些算法有超線性加速比，一些則沒有。Papaefthymiou和Rodrigue在CM-5上實現了Bellman-Ford-Moore算法，并比較了粗粒度劃分和細粒度劃分之間的差異。此外，其他衍生出來的算法，還有平衡二叉樹的標簽設定算法、單隊列的標簽修正算法、雙隊列的標簽修正算法等。本文基于多進程環境把Dijkstra串行算法轉化為并行算法，該算法采用按列分塊，適合于無向圖或有向圖的求解。

2 Dijkstra并行算法的設計

設圖G(V，E)是一個有向加權網絡，其中V是頂點的集合，E是邊集合。使用連接矩陣W來表示圖，邊上權 值 w[i][j]>0,i,j∈V，V={0，1，…，n-1}，dist(i)表 示 為最短路徑長度。

2.1 數據劃分

為了使程序由各個處理器獨立地執行，必須要找到可以并行性的操作。

常用的數據劃分方法有行劃分、列劃分和分塊劃分等。由于每次內循環都要使用到某一定點到其他頂點的權值，而且當圖G(V，E)是有向圖的時候，權值矩陣非對稱，因此此算法不適宜使用行劃分。在此使用按列分解的方法。

分別為每個處理器分配若干的節點求得局部最小值，然后再將各個處理器求得的最小值進行歸約，將歸約得出的最小值廣播到每個處理器中。

為了得到一種能夠負載平衡的數據分解方法，可以對每個進程分配?n/p」或「n/p?個元素。這里使用的是按列分解方法，假設有節點數目是n，進程數是p，進程 i控制的第一列是?in/p」，進程 i控制的最后一列是?(i+1)n/p」-1，對于特定的列 j，控制它的進程是?(p(j+1)-1)/n」，任意兩個進程控制的列數相差不會超過1。數據分割的結果如圖1所示。

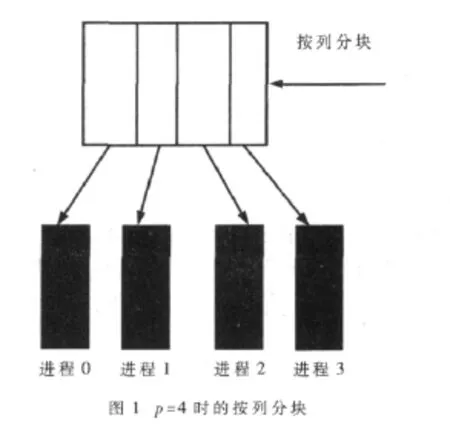
按圖1所示的數據劃分，則分布在不同進程i上的數據分別是 w(n，i×n/p：(i+1)×n/p-1)，其中 i×n/p：(i+1)×n/p-1代表取第 i×n/p列到第(i+1)×n/p-1列的數據。

2.2 Dijkstra并行算法實現

Dijkstra并行算法偽代碼可表示為：

(1)MPI_Init(&argc，&argv)；

(2)MPI_Comm_size(MPI_COMM_WORLD，&p)；

MPI_Comm_rank(MPI_COMM_WORLD，&my_rank)；

(3)0處理器讀入鄰接矩陣和起始點s，分發鄰接矩陣到各個處理器，廣播s。

(4)//初始化各個處理器的數據

(5)//每次循環分別求出到達一個結點的最小值

③/*通信域中的每一個進程通過local結構把它的（數值、下標）對傳遞給MPI_Allreduce。當函數返回時，最小值和相關的下標存放在global結構中。

④//更新源點s到每個頂點的距離

⑤//把頂點 global.index對應處理器的//bdist[i]值改為true

⑥MPI_Barrier(MPI_COMM_WORLD)；

(6)輸出各個處理器求出的dist[i]值。

(7)MPI_Finalize()；

3 算法分析

3.1 算法復雜度

串行版本的Dijkstra算法的時間復雜度為O(n2)。

初始化各個處理器數據的時間復雜度為 O(n/p)，在算法的內循環①部分求出局部最小值以及相應的索引，最多執行「n/p?次，因此時間復雜度為 O(n/p)；③部分對一個長度為1的數據進行全歸約。由于歸約p個處理器需要「log2p?個消息傳遞步驟，總的時間復雜度為O(「log2p?)；④更新源點到其他頂點距離的時間復雜度為O(n/p)；⑤更新最小值對應的bdist[i]需常數時間。

最外層執行n-1次。

因此，并行算法的總的時間復雜度為：

即O(n2/p+nlog2p)

3.2 加速比和效率

設Ψ(n，p)表示為p個處理器上解決問題規模為 n的問題的加速比，ε(n，p)表示為在 p個處理器上解決規模為n的并行計算效率。作以下定義：

定義1：加速比=串行執行時間/并行執行時間。

定義2：效率=加速比/使用處理器數。根據定義得到：

隨著數據規模的增大，計算量增加速度比通信量開銷增加更快，因此該系統隨著數據規模的增大可以取得更好的加速比和效率值。

3.3 等效指標

在研究中發現并行算法可以分為以下3類：

(1)必須串行執行的計算，用 σ(n)表示；

(2)可以并行執行的部分，用 φ(n)表示；

(3)并 行 開 銷(通 信 操 作 和 冗 余 計 算)， 用 κ(n，p)表示。則得出一個加速比的完整的表達式為：

定義T0(n，p)代表所有進程花費在原有串行算法以外操作的全部時間。其組成是(p-1)個進程花在進程的內在串行部分的時間，以及p個進程花費在處理器通信和冗余計算上的時間。 所以將 T0(n，p)=(p-1)σ(n)+pκ(n，p)代入上式，得到：

T(n，1)代表串行執行時間，即：

如果效率不變，那么 ε(n，p)/(1-ε(n，p))是一個常數，上面公式可以化為：

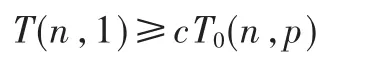
由于在處理器個數增加時并行開銷會增大，因此要保持效率就要增加問題的規模。假定一個并行系統具有等加速比關系：n≥f(p)。如果M(n)表示規模為n的問題所需的內存大小，M-1(n)≥f(p)則表示為了保持效率不變所需的內存與處理器個數p的函數關系。M(f(p))/p稱為可擴展函數，其復雜度確定了可保持常數效率的處理器個數范圍。

Dijkstra串行算法的時間復雜度是O(n2)。并行算法中全歸約的復雜度是O(nlog2p)，每個處理器都參與了此步驟，因此

T0(n，p)=O(nplog2p)，因此并行算法的等效關系為：

串行算法中問題規模n所需的內存容量為n2，即M(n)=n2，此系統的可擴展性函數為：

即每個處理器的容量隨p增加。由于內存容量的限制,處理器的個數不能一直增加，因此此系統處理器的個數應在內存允許的范圍之內才能取得最好的效果。

本文在mpi環境下設計了求單源點最短路徑的Dijkstra并行算法，分析了該算法的時間復雜度、加速比、效率以及等效指標。理論證明了利用多處理器共同計算的優點，使若干臺計算機就能完成大型計算機所完成的計算功能，解決了單計算機內存不足的問題，降低了計算成本，提高了程序的效率。在實際應用中，還要考慮到計算機之間的通信速度，這對計算性能的提高與否有重大影響。并行計算在未來的大規模計算中也會日益發揮重要的作用，如何提高并行性和進一步減少通信開銷是將來要改進的工作。

[1]袁貞明，張量.GIS的前k個最短路徑分布式多線程實現[J].計算機工程，2005，31(9)：37-38，162.

[2]COHEN E.Efficient parallel shortest-paths in digraphs with a separator decomposition[J].Algorithms，1996(21)：331-357.

[3]TRAFF J L，ZAROLIAGIS C D.A simple parallel algorithm for the single2source shortest path problem on planar digraphs[J].Journal of Parallel and Distributed Computing，2000，60(9)：1103.

[4]ADAMSON P，TICK E.Greedy partitionecd algorithms for the shortest path problem[J].International Journal of Parallel Programming，1991，20：271-298.

[5]TRAFF J L.An experimental comparison of two distributed single-source shortest path algorithmns[J].Parallel Computing，1995，21：1505-1532.

[6]ROMEIJN H E，SMITH R L.Parallel algorithms for solving aggregated shortest path problems[D].The University of Michigan，September 1993.

[7]BERTSEKAS D，GUERRIERO F，MUSMANNO R.Parallel asynchronous label-correcting methods for shortest paths[J].Journal of Optimization Theory and Applications，1996，88：297-320.