圓錐滾子軸承振動因素分析的定性融合方法

夏新濤，張 林，劉勁軍

（1.河南科技大學機電工程學院，河南洛陽471003;2.洛陽軸研科技股份有限公司，河南洛陽471039）

1 前言

圓錐滾子軸承應用廣泛，是生產與使用數量僅次于深溝球軸承的第二大類軸承產品，主要用于汽車、數控機床、電機等重點主機配套。進入20世紀90年代中后期，隨著社會發展和配套主機性能的不斷提高，特別是作為小型、中小型圓錐滾子軸承主要用戶的國產輕型轎車生產企業，對此類軸承的振動質量狀況已提出越來越高的要求，以至于與要求較高的國產主機、出口主機配套用軸承或進口主機的維修用軸承均采用進口。圓錐滾子軸承的振動性能水平已成為制約提高此類軸承總體質量水平的瓶頸。

國內對滾動軸承振動與噪聲的研究開始于20世紀60年代[1-4]。半個世紀以來，我國在軸承減振降噪方面做了許多工作，軸承振動與噪聲有了大幅度下降[5-13]。但軸承行業對軸承振動與噪聲的研究主要集中在深溝球軸承產品，經過多年的努力，特別是“九五”期間大量的基礎研究和技術攻關，使深溝球軸承的加工制造不斷精化，技術水平不斷提高，振動與噪聲的控制能力與其他類型的軸承產品（例如圓錐滾子軸承）明顯拉開了檔次，已開始進入產業化階段。與之相比，滾子軸承的減振降噪工作開展得一直比較薄弱，質量水平一直在低水平上徘徊，與國外名牌產品之間的差距也較大，僅從批量生產的圓錐滾子軸承振動與噪聲來看，我國同類產品的先進水平比國外先進水平的振動值要差1～3個振動級別，軸承振動的穩定性也比較差。這已成為困擾許多滾子軸承生產企業的一大難題[5-15]。

影響圓錐滾子軸承振動加速度的因素很多[15]，本文主要考慮套圈和滾子的加工質量參數。加工質量參數很多，必須有針對性地抓住其中的主要因素，才能有效地控制軸承振動加速度值。另外，考慮試驗成本，生產現場抽樣個數比較少。如何在有限的數據個數條件下尋找出最重要的因素，就成為問題的關鍵。

根據滾動軸承乏信息試驗分析與評估原理[15-21]，比較可靠的措施是用多種數學方法研究，得出多種結果。由于每一種結果都有其局限性，因此應對這些結果進行對比分析和融合，得出具有共性的一個結論，這個結論就是影響圓錐滾子軸承振動加速度的最重要因素，即問題的最終解，這就是定性融合方法[15]。

2 定性融合原理

定義定性融合[15]是指，在給定的論域U中，已知解集

且有

式中：

F0—系統屬性的真值集合即白箱問題，

|—在準則下，

|From F—來自解集F元素。

由于系統信息或數據的不完備性，因此，用不同的數學方法分析，將得出不同的結果fi，甚至有些結果可能是相互矛盾的。若將這些結果看成一個個解的集合即解集F，則定性融合是指，在某種準則下，從這些解集中提取具有某種一致性元素的子集，并將這個子集作為系統的最終解f0。

定性融合有兩個方面的含義：一是融合，即綜合考慮各個解集；二是定性，即不再進行復雜的數學計算，只是尋求某種一致性，而且，最終解中的元素全部來自解集F，沒有更新的信息出現。

例如，在一定約束條件下，對某個系統進行優化分析，考慮了3個指標：成本a、環境污染b和危險性c。設這些指標可以用當量數據表示，數據的值越小越好。即優化目標集f為 f=(a,b,c)→min

假設用4種數學方法求解，得到4個解集，分別為

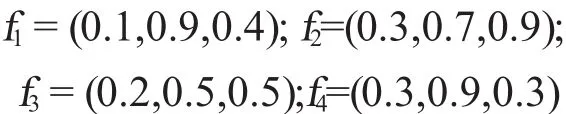
則解集F為

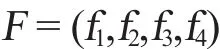
顯然，在解集F中，對應最小a的是f1中的0.1；對應最小b的是f3中的0.5；對應最小c的是f4中的0.3。于是得到一個子集：

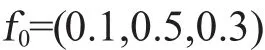
如果f0滿足約束條件，那么，它就是系統的最優解；否則，就以f0為模板（即準理想解集，也叫靶心），再進行對比分析，將最接近f0的fi作為最終解。顯然，f0中的元素均來自解集F。

3 用于軸承性能影響因素分析的定性融合方法

設憑經驗知道有N個相互獨立的因素（例如結構參數和潤滑條件等）可能會影響滾動軸承的性能（例如振動或疲勞壽命等）P，有因素符號集X為

用m種數學方法對試驗數據進行處理，得到m個影響因素排序集（因素的影響從大到小排序，對性能影響越大的因素，其符號位置越靠左）即對于性能P，有

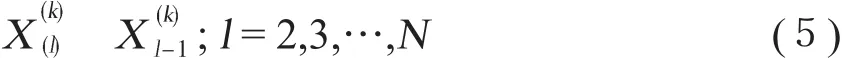
于是得到排序因素符號矩陣：

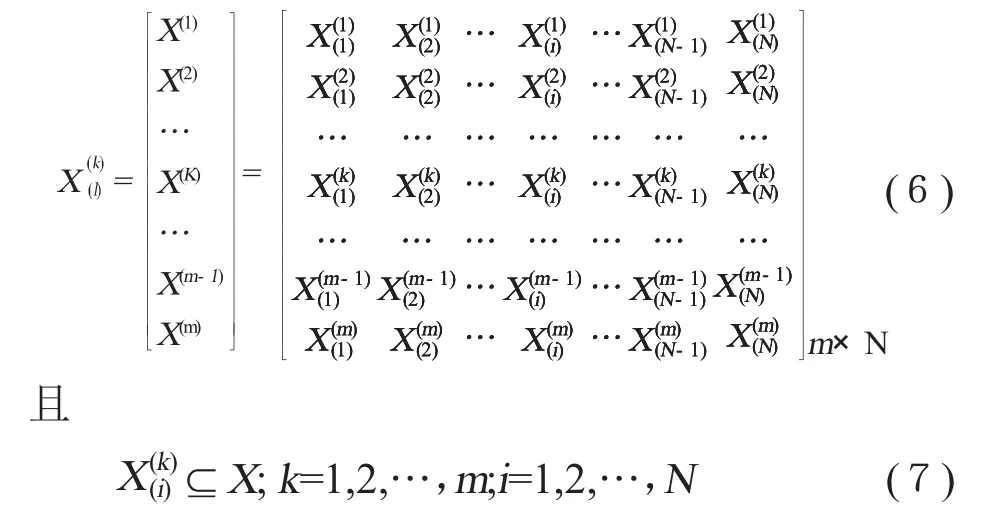
式中， 表示優于，X表示某因素，(i)表示排序序號，(k)表示用第k種數學方法計算。

在m個因素排序即矩陣X(k)(i)中，各挑出n≤N個位置靠左的因素符號，即矩陣X(k)(i)中的前n列，作為解集F：

則最終解f0為F中均具有的因素的集合（符號）即

若基數

即

則定性融合有唯一解。

在最終解f0中，s個因素是不分前后順序的，它們都是影響軸承性能P的主要因素，將它們改用新的符號并重新編號，有

在以上分析中，一般n的大小取

可以看出，因f0X，故在f0中沒有新信息。

4 解集獲取的方法

為便于研究，設軸承振動加速度值X0構成的數據序列為影響因素Xi構成的數據序列為

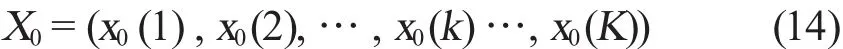
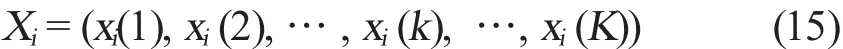
式中，K是數據個數。

4.1 灰色關聯方法

灰色關聯分析主要是根據測量數據序列之間的幾何形狀的相似性，來評價各數據序列之間關聯性。

在試驗數據處理中，灰色系統理論具有傳統統計理論無法比擬的優點：所需要的數據量很小，也不要求這些數據符合典型的概率分布，而且所得結果一般不會與定性分析結果產生矛盾，這也就是說，在很少的試驗數據及所研究系統的概率未知的情況下，灰色系統理論的計算結果可以充分體現所研究系統的內在規律。目前，灰色系統理論在軸承振動與噪聲的研究中已經得到了初步的應用，并取得了一定的成果[15-21]。

由于由圓錐滾子軸承的各參數與振動值組成的系統中各因素的物理意義不同，各指標原始數據的量綱也不一定相同，有的數值的數量級相差懸殊，這在比較時就難以得到正確的結果。因此，在計算前需要對原始數據進行無量綱化處理，從而使原始數據轉化為可以比較的數據列。主要利用均值化處理對數據進行了預處理。灰色關聯方法的處理步驟如下。

第1步均值化變換。計算公式：

第2步 求在各點上X0與Xi的關聯系數L0i(k)，計算公式：

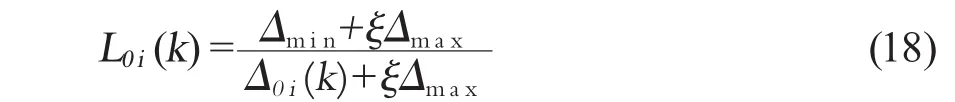
式中

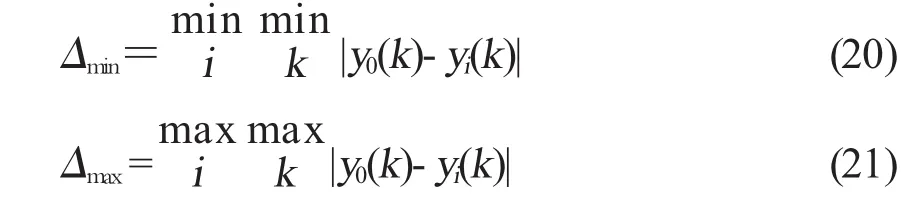
式中，ξ是分辨系數，ξ∈(0,1)。

第3步求關聯度。計算公式：

第4步排關聯序。將m個子序列對同一母序列的關聯度按大小順序排列起來，即組成關聯序，它直接反映了各個子序列對同一母序列的“優劣”或“主次”關系。若γ0a＞γ0b，則稱子序列Xa對于相同母序列X0有優于子序列Xb的特點。

4.2 灰色絕對關聯度方法

設序列X0與Xi的長度相同且初值皆不為零，那么可以用灰色絕對關聯度來表征X0與Xi的相對始點的幾何形狀之間的關系，若X0與Xi的幾何形狀越接近，那么它們的絕對關聯度越大。灰色絕對關聯度計算步驟如下。

第1步初值零化處理。

第2步計算絕對關聯度。

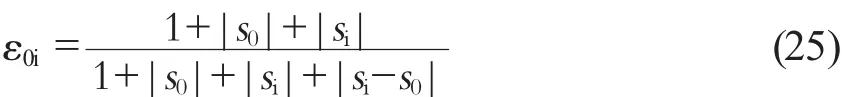
式中

灰色絕對關聯度ε0i具有下列性質：

(1)0＜ε0i≤1；ε0i恒不為零，表明任何兩個序列都不是絕對無關的；

(2)ε0i只與Xi和X0的幾何形狀有關，而與其相對位置無關，也就是說，平移不會改變絕對關聯度的值；

(3)ε0i越小，Xi和 X0的相似程度越小，聯系越不密切；

(4)ε0i越大，Xi和 X0的相似程度越大，聯系越密切；

(5)ε0i=1，表明Xi和X0完全一樣，無任何區別。

4.3 灰色相對關聯度方法

第1步計算初值像。

第2步求始點零化像。

第3步計算灰色相對關聯度。

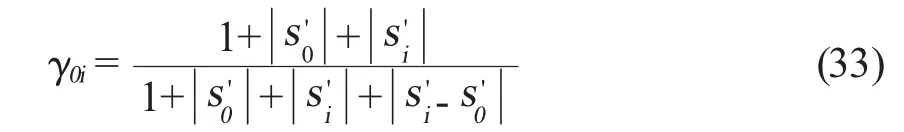
式中

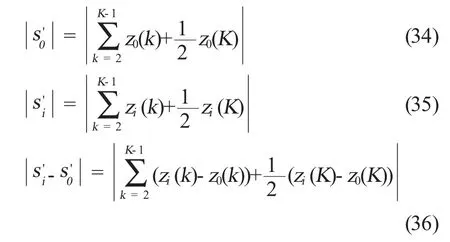
計算出灰色相對關聯度，從而進行排序分析。

灰色相對關聯度具有下列性質：

(1)0＜γ0i≤1；γ0i恒不為零，表明任何兩個序列都不是絕對無關的；

(2)γ0i可以表示Xi和X0相對初始點的變化速率之間的關系，Xi和X0的變化速率越接近，就越大，反之就越小；

(3)γ0i=1，表明Xi和X0完全一樣，無任何區別。

5 圓錐滾子軸承振動加速度影響因素的試驗研究

研究上海某軸承企業生產的30204型圓錐滾子軸承的振動加速度問題。通過試驗來研究軸承內外圈和滾動體的參數與軸承振動之間的關系，以尋求控制軸承振動質量的乏信息方法[15,17]。

確定了軸承的16個套圈參數和16個滾子參數共計32個參數作為研究對象。通過試驗研究軸承的各項參數與軸承振動之間的關系。

為方便研究，在表1中給出試驗研究所使用的符號及其含義。為便于敘述，用“差”代表一套軸承中15個滾子該項參數的極差，“均”代表一套軸承中15個滾子該項參數的均值，用“內”代表內圈滾道，用“外”代表外圈滾道。

表1 符號

試驗用軸承振動加速度X0的測量結果為（dB）

參數X1～X32的試驗數據略（具體細節見[15,17]）。

5.1 灰色關聯度的計算結果

取ξ=0.5，得各參數與振動值的關聯度排序如下

5.2 灰色絕對關聯度的計算結果

根據灰色絕對關聯度法，得各參數與振動值的絕對關聯度排序如下

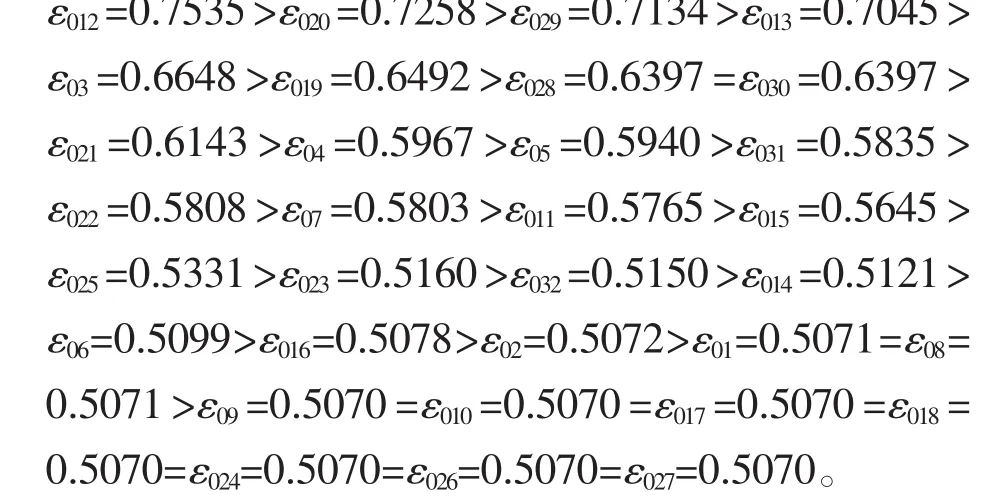
5.3 灰色相對關聯度的計算結果

根據灰色相對關聯度法，得各參數與振動值的相對關聯度排序如下

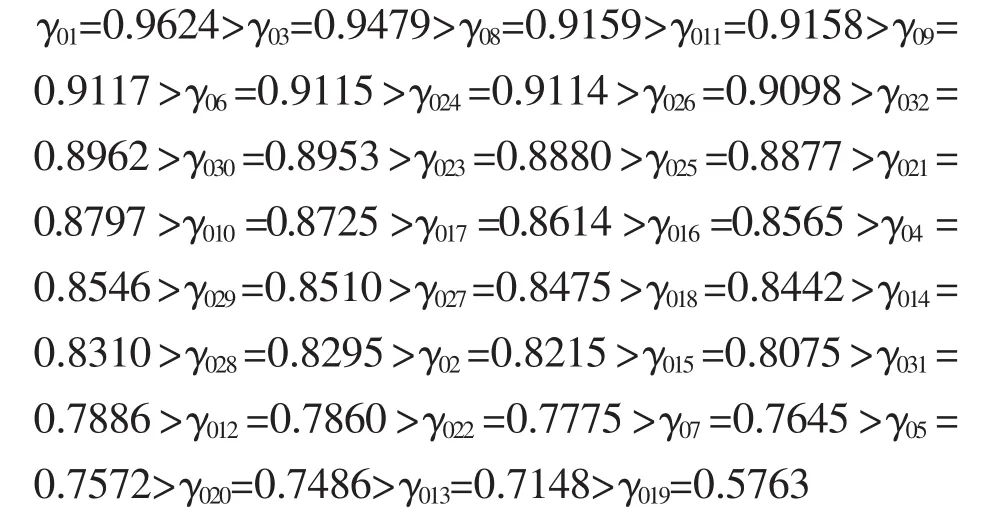
6 討論

將以上3種方法排序結果中前16個取出，用因素符號Xi表示在表2中。

表2 三種方法排序結果中的前16名

根據式(9)，得最重要的因素集合為

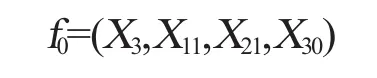
在3種數學方法的排序結果中，將前16名作為可能的重要因素。前16名出現的頻數和影響程度分別見表3和表4。將表4中的影響因素進行分類，結果見表5。

表3 在三種數學方法排序中前16個因素出現的頻數

表4 在三種數學方法排序中前16個因素對軸承振動加速度的影響程度

如表4和表5所示，總體看來共有28個主要因素，其中滾子質量參數14個，內圈質量參數8個，外圈質量參數6個。因此，對于試驗用軸承而言，3個零件對振動加速度的影響權重比為滾子/內圈/外圈=14/8/6≈2.3/1.3/1

從最重要因素和第二重要因素中發現，共有16個主要因素，其中滾子質量參數8個，內圈質量參數4個，外圈質量參數4個。因此，對于試驗用軸承而言，3個零件對振動加速度的影響權重比為

滾子/內圈/外圈=8/4/4=2/1/1

從最重要因素中發現，共有4個主要因素，其中滾子質量參數2個，內圈質量參數1個，外圈質量參數1個。因此，對于試驗用軸承而言，3種零件對振動加速度的影響權重比為

滾子/內圈/外圈=2/1/1

因此，在測量條件下，對試驗軸承振動加速度貢獻最大的是滾子，其次是內圈和外圈。得到這個結論的一個主要原因是滾子質量參數最多，內圈次之，外圈最少（見表1和表5）。

表5 主要影響因素按誤差類型分類

7 結論

推薦了基于乏信息系統理論的定性融合方法，以尋找影響圓錐滾子軸承振動加速度的最重要因素。

試驗研究發現，在測量條件下，對滾子而言，圓錐表面母線凸度是試驗軸承的最薄弱環節。這說明凸度的形狀、大小與加工質量對軸承振動加速度有重要影響；對內外圈而言，滾道圓度誤差是試驗軸承的最薄弱環節。這4個質量參數均為宏觀誤差參數。

[1]Tallian LD,Gustafsson OG.Progressin rollingbearingvibration researchandcontrol[J].ASLETrans,1965，8(3)：195～207.

[2]小林政弘,橋本正義.滾動軸承的噪聲和振動問題(2)[J].機械的研究,1968,20(2)：316～320.

[3]Oswald B.Noiseand Vibrational Behaviour of Rolling Bearing,Ball and Roller Engineering[J].Industrial Engineering(FAG),1989，28：4～11.

[4]Tandon N,Choudhury A.A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings[J].Tribology International,1999,32：469～480.

[6]夏新濤.滾動軸承磨削諧波控制理論及應用[M].北京：兵器工業出版社,2000.

[7]夏新濤,王中宇,孫立明,等.滾動軸承振動與噪聲關系的灰色研究[J].航空動力學報,2004,19(3)：424～428.

[8]賴俊賢,徐慧娟,劉海嬰.滾動軸承振動與噪聲[J].軸承,2001,(9)：37～40.

[9]馬純,劉春浩,趙聯春.滾動軸承的結構振動[J].哈爾濱軸承,2003,24(2)：17～22.

[10]張永恩,李興林,曹茂來.NSK低振動及低噪聲新產品技術[J].軸承,2003,(8)：45～46.

[11]劉壽祥,沈國祥,呂亞芳.降低圓錐滾子軸承[J].軸承,1999,(8)：38～41.

[12]商錦海.圓錐滾子軸承振動值分析[J].軸承,2000,(8)：32～33.

[13]姜利平.降低滾子軸承振動值及噪聲的措施[J].軸承,2004,(4)：17～18.

[14]夏新濤,馬偉,頡潭成,等.滾動軸承制造工藝學[M].北京：機械工業出版社,2007.

[15]夏新濤,陳曉陽,張永振,等.滾動軸承乏信息試驗分析與評估[M].北京：科學出版社,2007.

[16]苗曉鵬.圓錐滾子軸承振動的試驗研究[D].洛陽：河南科技大學,2005.

[17]劉勁軍.圓錐滾子軸承減振降噪研究[D].洛陽：河南科技大學,2006.

[18]苗曉鵬,夏新濤.圓錐滾子軸承套圈參數與振動關系的灰色研究[J].四川冶金,2005,(3)：46～47.

[19]劉勁軍,夏新濤,等.圓錐套圈參數對振動影響的模糊集合貼近度分析[J],軸承,2006,(8)：23～26.

[20]苗曉鵬,夏新濤.基于灰色系統理論的圓錐滾子軸承振動控制方法研究[J].機床與液壓,2006,(7)：236～237.

[21]苗曉鵬,夏新濤.圓錐滾子軸承振動研究[J].機床與液壓,2006,(8)：8～10.