應力錐橡膠材料在變溫環境下的力學性能

魯中亞, 馬永其,2, 徐 操

(1.上海大學上海市應用數學和力學研究所,上海 200072;2.上海大學理學院,上海 200444;3.上海三原電纜附件有限公司,上海 201206)

應力錐橡膠材料在變溫環境下的力學性能

魯中亞1, 馬永其1,2, 徐 操3

(1.上海大學上海市應用數學和力學研究所,上海 200072;2.上海大學理學院,上海 200444;3.上海三原電纜附件有限公司,上海 201206)

利用德國 Zwick020材料試驗機,進行高壓電纜終端應力錐兩種橡膠材料在不同溫度環境下單向拉伸大變形力學行為的試驗研究,得到不同溫度和不同加載速率條件下材料的應力-應變關系曲線,并分析了溫度及加載速率變化對材料力學性能的影響.運用Mooney-Rivlin橡膠材料模型,對試驗材料進行了理論分析,根據試驗結果擬合出相關參數,構建了適用高壓電纜終端應力錐兩種橡膠材料的本構關系公式.對比不同溫度下兩種橡膠材料的理論計算和試驗的應力值,說明該本構關系滿足工程實際需要,為高壓電纜應力錐的進一步研究提供了理論基礎.

橡膠材料;應力錐;本構關系;拉伸試驗

Abstract:Mechanical behavior of large-scale deformation for rubber stress cone of high voltage cable accessorieswas studied with a German Zwick020 material testmachine.Stress-strain relation curveswere obtained under different temperatures and different loading rates. From these curves,influences of temperature and loading rate were analyzed.The material’s mechanical properties were theoretically analyzed with the Mooney-Rivlin model,and some fitting parameters of the material were got from experimental data.Two constitutive equationsof materialwere then constructed,and the stressobtained in the experiment was compared w ith theoretical calculation. It show s that the equations are suitable in engineering practice and can be used for further research.

Key words:rubber;stress cone;constitutive relation;tensile test

近年來,隨著我國經濟的發展,電力的安全可靠供應越來越重要.北京奧運會舉辦之前,國家電力監督委員會專門組織開展電力行業安全生產百日督查專項行動,以確保用電安全.現今,我國遠距離輸電線路都采用高壓架空線,而在大城市等人口稠密地區的輸電網絡和發電廠、大型工廠、交通擁擠的地方大多采用電力電纜[1].電力電纜是用于電力傳輸和分配的電纜[2].我國電纜制造行業通過引進國外技術、設備和原材料,已有了飛速的發展,但是電纜附件本身結構、制作和連接及運行條件復雜,導致其發展相對滯后.在電力系統故障發生的概率中,電纜附件的故障占到電纜運行故障的 50%以上[3],所以電纜附件的運行安全是關系到整個電網正常運轉的重要因素.國內外新建設的高壓電纜工程,大多采用預制型電纜終端[4],它是一種較先進的電纜終端,已得到了廣泛應用,是目前和將來高壓電纜終端技術應用的主流[5].

預制型電纜終端的高效安全運行,需要使橡膠預制應力錐和環氧樹脂套管、電纜絕緣之間的界面緊密接觸,并保持一定的界面應力.預制型電纜終端的界面應力,主要由彈簧壓緊裝置的機械力和橡膠應力錐擴張后產生的箍緊力兩部分組成.研究表明,當界面壓力增大時,界面的電場擊穿強度也隨之增大,密封度也升高[6],因此,維持滿足設計要求的界面應力是預制型電纜終端正常工作的關鍵所在.在運行過程中,高壓電纜終端承受著交變荷載,電纜芯溫度最高可以達到 90℃,高電場、高熱場都會加速橡膠的老化.此外,絕緣油的滲漏還會引起應力錐材料溶漲,最終都會導致界面應力的變化[7].本研究主要分析橡膠錐的橡膠材料性能與擴張后產生的箍緊力大小的關系,通過試驗研究獲得高壓電纜終端應力錐橡膠材料的應力應變關系,根據試驗數據擬合出材料的應變能函數,構建出適用此兩種材料本構關系的公式,為進一步研究橡膠應力錐的老化和疲勞導致的可靠性降低奠定基礎.

1 試 驗

1.1 試驗裝置

高壓電纜終端應力錐橡膠材料單向拉伸試驗采用帶溫箱的德國產 Zwick020材料試驗機,最大載荷2 t,電阻加熱溫箱內的最高溫度可達 250℃,加載速率范圍為 0.000 5～1 000 mm/min.試驗加載過程由微機自動控制,在試驗過程中,如載荷為零,試驗機會自動終止試驗.試驗操作過程根據 GB/T 258—1998標準進行,外加載荷和試件變形由試驗機自行測量并記錄,最后通過應力-伸長率關系曲線表示.試驗機溫箱的升溫速率約為 8℃/min.

1.2 試件

高壓電纜終端應力錐橡膠材料包括兩種:絕緣橡膠和半導電橡膠.將兩種橡膠材料根據GB/T 258—1998標準制成啞鈴狀試驗材料試件,橡膠材料試件厚度為 2 mm.試驗段長 25 mm,寬 6 mm.

1.3 試驗過程

為提高試驗的效率,更好地模擬實際運行工況下橡膠應力錐所處的環境溫度,本研究將試驗進行如下設計.假設常年室外平均溫度為 20℃.在 20,60,70,80,90,120℃均依據 GB/T 258—1998標準,以 500 mm/min的加載速率進行單向拉伸試驗.電纜芯在 110,220 kV工況運行時,內部溫度分別為 70和 90℃左右,為更好地反映橡膠應力錐的橡膠材料在工作時所處的溫度環境對其力學性能的影響,在70,90℃溫度下的試驗中,除以 500 mm/min的標準加載速率進行加載外,另分別增加 1組以 300 mm/min為加載速率的對比試驗.

1.4 試驗結果及分析

一般情況下,橡膠材料為不可壓縮彈性體[9-10],在單向拉伸狀態下,不可壓縮橡膠材料的主伸長分別為

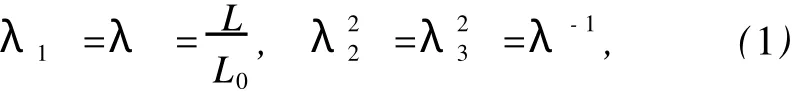
式中,λ為試件在拉伸方向的主伸長,L0和 L為試件試驗有效段的初始長度和最終長度.橡膠材料的主應力分別為

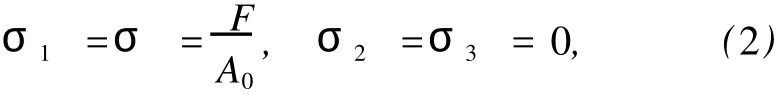
式中,F為施加的荷載,A0為有效段的初始橫截面面積.

試驗結果以應力 (MPa)-伸長率 (%)曲線表示,圖1、圖2分別為絕緣橡膠材料、半導電橡膠材料在500 mm/min加載速率和不同溫度下的應力-伸長率曲線.圖3、圖4分別為絕緣橡膠材料在 70,90℃溫度下兩種加載速率的應力-伸長曲線.圖5、圖6分別為半導電橡膠材料在 70,90℃溫度下兩種加載速率的應力-伸長曲線.

由圖1～圖6可見,首先,絕緣橡膠材料和半導電橡膠材料力學性能相差很大.絕緣橡膠材料的應力-伸長率曲線變化速率快、應力值大,這說明絕緣橡膠更難以拉伸,更加堅硬.這種性質與絕緣橡膠在外部起絕緣和保護作用是有密切關系的.

其次,兩種橡膠材料都對溫度比較敏感,其力學性能強烈依賴于溫度,但是兩種材料的應力-伸長率變化規律又不同.如圖1所示,絕緣橡膠材料在相同的伸長率下,在 20℃時應力最小,在 60℃時應力最大,隨著溫度的升高應力依次減小,但不會小于20℃時的應力.如圖2所示 ,半導電橡膠材料在 20℃時應力最大,隨著溫度的升高應力也依次減小,在 120℃時為最小.這是因為隨著溫度的升高,導致分子間作用及鏈段間作用削弱[11],在高溫段出現軟化,材料剛度降低,在相同伸長率下,應力減小.最后,在相同的溫度下,材料剛度隨著加載速率的增大而增大.這是因為橡膠材料的高分子鏈結構的充分伸展需要一定時間,隨加載速率的減小,橡膠的高分子鏈結構能夠得以充分伸展[11].在應力緩慢增加的條件下,伸長率得以快速增加,在相同的伸長率下應力減小.

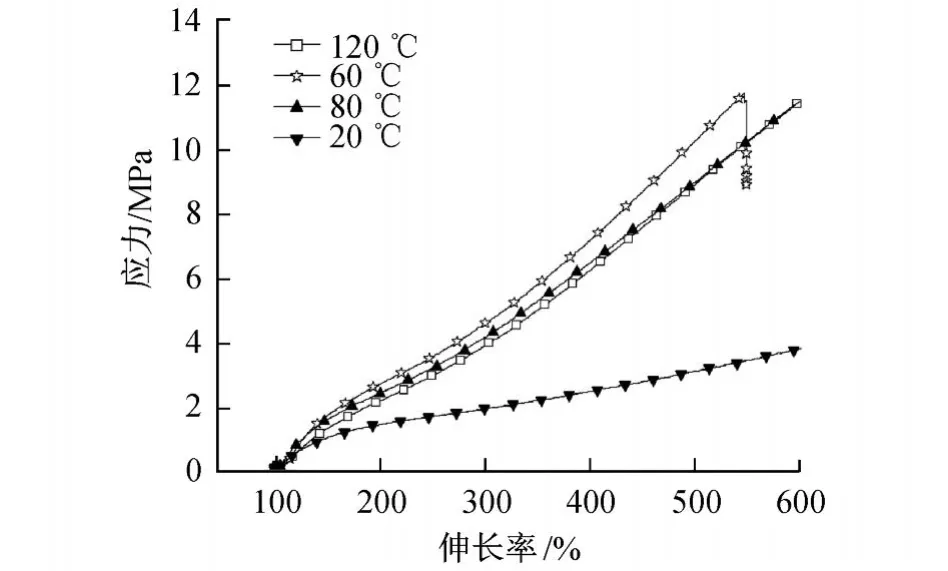
圖1 絕緣橡膠材料在 500 mm/m in加載速率下應力-伸長率曲線Fig.1 Stress-strain relation curves of insulating rubber under 500 mm/m in

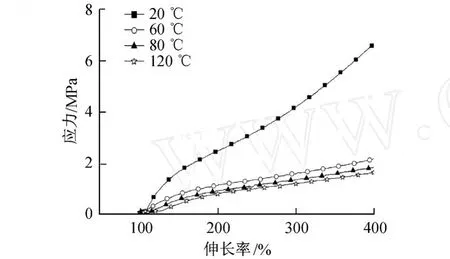
圖2 半導電橡膠材料在 500 mm/m in加載速率下應力-伸長率曲線Fig.2 Stress-strain relation curves of sem i-electr ic rubber under 500 mm/m in

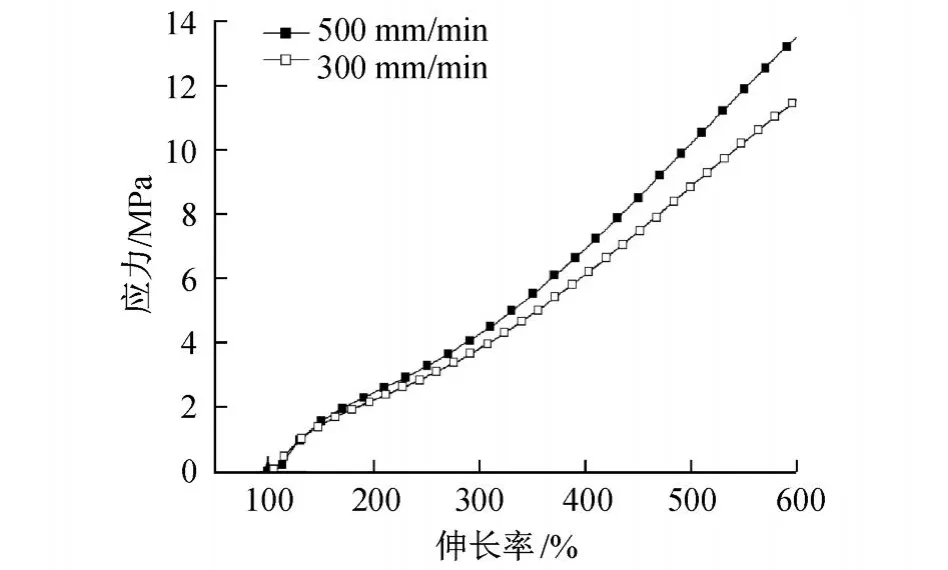
圖3 絕緣橡膠材料在 70℃、不同加載速率下應力-伸長率曲線Fig.3 Stress-strain relation curves of insulating rubber under d ifferent load ing ratesat 70℃

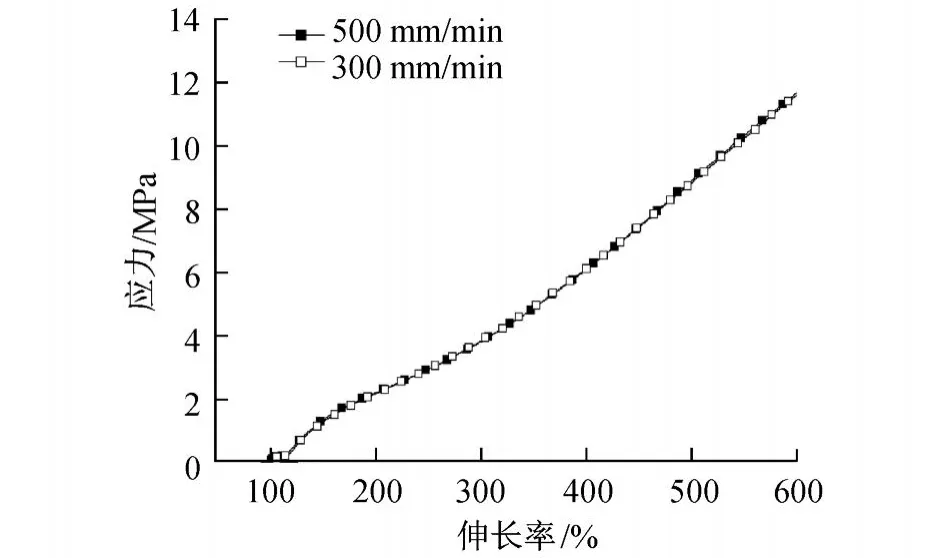
圖4 絕緣橡膠材料在 90℃、不同加載速率下應力-伸長率曲線Fig.4 Stress-stra in relation curves of insulating rubber under d ifferent load ing ratesat 90℃

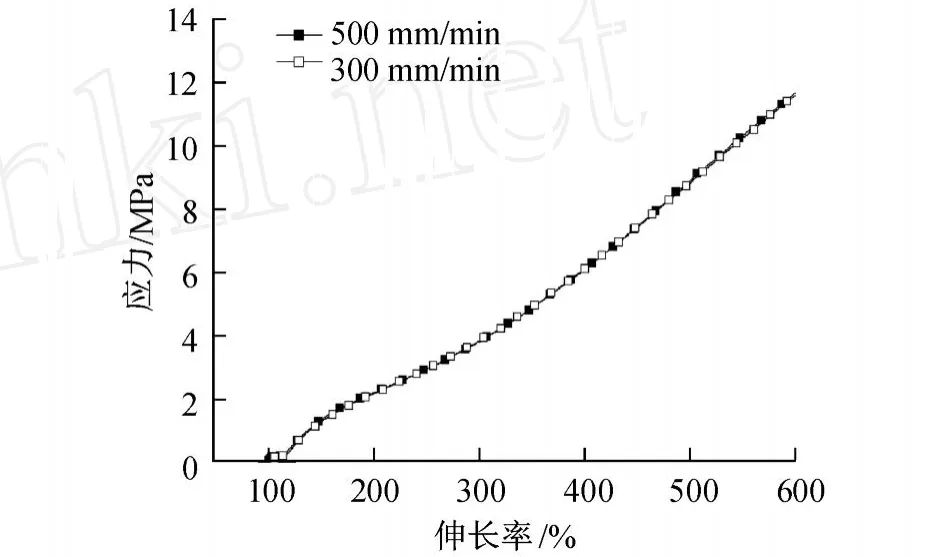
圖5 半導電橡膠材料在 70℃、不同加載速率下應力-伸長率曲線Fig.5 Stress-stra in relation curves of sem i-electr ic rubber under d ifferent load ing ratesat 70℃

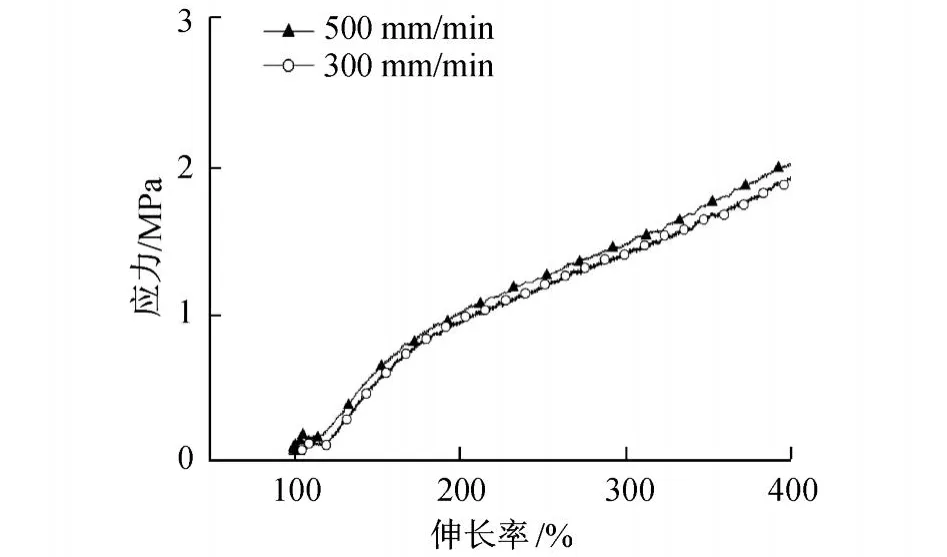
圖6 半導電橡膠材料在 90℃、不同加載速率下應力-伸長率曲線Fig.6 Stress-stra in relation curves of sem i-electr ic rubber under d ifferent load ing ratesat 90℃

2 不可壓縮超熱彈性體本構關系理論分析

按照Mooney-Rivlin方程[12],不可壓超彈性材料應力-應變關系可以表示為

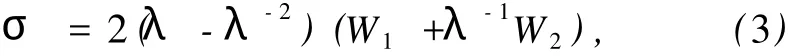
式中,W=W(I1,I2)為材料的應變能函數,I1,I2分別為材料變形張量的第一和第二不變量,W1,W2表示應變能函數對第一和第二不變量的偏導數.Gregory[13]注意到在單軸拉伸應力應變數據之間存在一個簡單的比例關系,但必須滿足下列兩個條件:① ?W/?I1? ?W/?I2;② ?W/?I2與 I2無關.

根據最小二乘法,對 60℃下標準加載速率獲得的應力-伸長率曲線進行擬合,可以得到該溫度下的C1,C2.C1在溫度不變時為常數,C2隨著應變的變化而變化[14],如表 1所示.

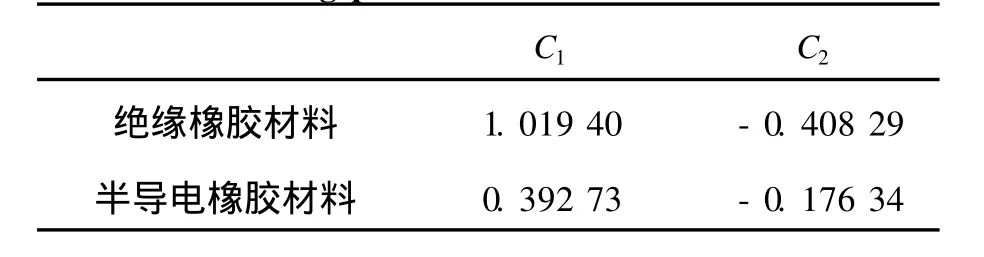
表 1 60℃時兩種橡膠材料相關參數Table 1 Fitting parameter s of two rubber sat 60℃

對不可壓熱超彈性材料,應變能函數的一般形式可以表示為[15]

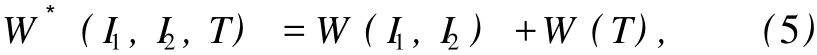
式中,W(I1,I2)為通常等溫情況下的應變能函數,W=W(T)描述溫度的影響,一般情況下可以寫為[16]

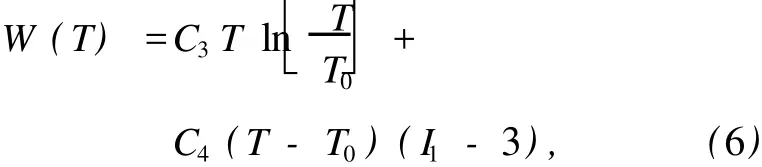
式中,T=T(R)為材料的溫度場,C3=Ce,C4=-αμ,Ce為材料的比熱容常數,α為材料的體積熱膨脹系數,μ為材料的第二拉梅常數,T0=300 K為參考溫度[17].由于沒有做絕緣橡膠和半導電橡膠相關物理性質參數的試驗,W(T)中的參數近似采用天然橡膠材料的相應常數[18],α=6.7×10-4K-1,μ=1.94 MPa,Ce=1 506 J·kg-1·K-1,材料實際密度ρ=870 kg·m-3,則最終相應的應力分量可以表示為

σ =2(λ -λ-2)[C1+λ-1C2+C4(T-T0)].(7)

由式 (7)得到理論計算值,與試驗結果的對比如圖7和圖8所示.

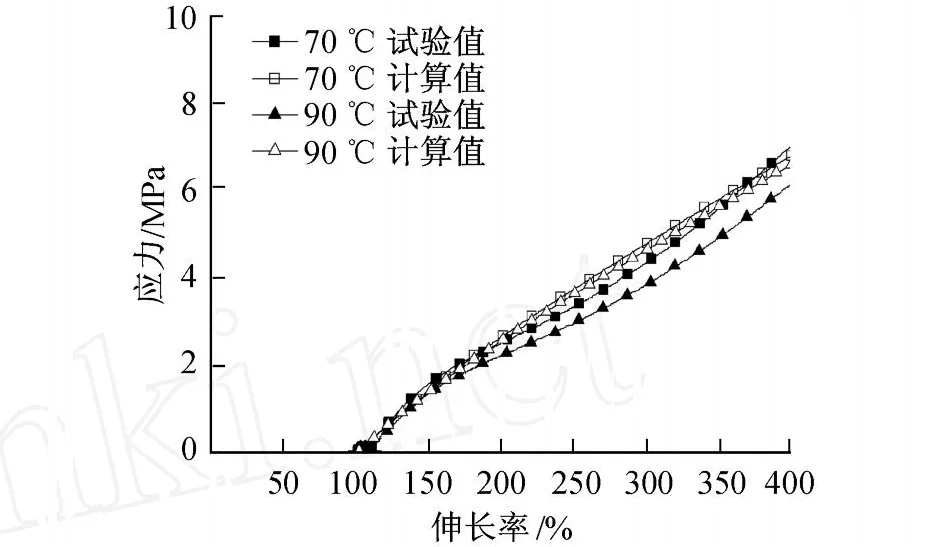
圖7 絕緣材料試驗結果與理論計算的應力值對比Fig.7 D ifferent between stress of exper iment and theoretical calculation of insulating rubber

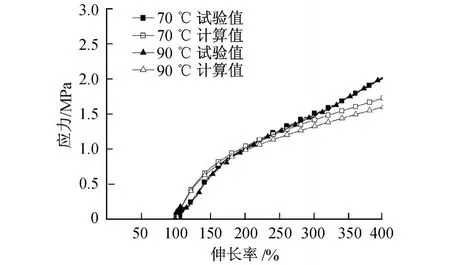
圖8 半導電橡膠材料試驗結果與理論計算的應力值對比Fig.8 D ifferen t between stress of exper im en t and theoretical calculation of sem i-electr ic rubber

圖7為絕緣橡膠材料分別在模擬實際工況下,應力-伸長率曲線的試驗值和理論計算值的比較.可以看出:在伸長率小于 200%時,理論計算值和試驗值可以很好地吻合;隨著伸長率增大,材料在大變形條件下,本構關系變化劇烈,理論計算數據和試驗值有一定的差距,這是由于采用相對簡單的 Mooney-Rivlin模型和直接采用天然橡膠的材料參數的原因.相關研究表明,Mooney-Rivlin模型可以較好地擬合不可壓縮橡膠材料中等應變范圍的應變能,不適用于壓縮及大應變時硬化的材料[19].但是,由于Mooney-Rivlin模型形式簡單,計算量小,同時高壓電纜終端應力錐在擴張時橡膠材料受拉伸幅度很小,因此,在伸長率小于 200%的范圍內,該本構關系公式很好地滿足了要求,可以運用到實際工程中.圖8為半導電橡膠材料的理論計算值和試驗值的應力-拉伸率的曲線圖,吻合情況與圖7類似.

3 結 論

(1)高壓電纜終端應力錐橡膠材料對溫度的變化非常敏感.隨著溫度的升高,兩種材料出現了明顯的力學性能改變,其中絕緣橡膠材料在 60℃時剛度最高,20℃時最小,且隨著溫度的繼續升高逐漸下降,因此,絕緣橡膠材料的剛度有一個先上升后下降的過程.但是,半導電材料不同,在相同的伸長率下,應力在 20℃時最大,且隨著溫度的升高依次下降.

(2)高壓電纜終端應力錐橡膠材料對加載速率非常敏感,加載速率越大,材料的剛度越大.試驗所用兩種橡膠材料均有上述特征.但是,隨著溫度的升高,受加載速率的影響降低,這說明溫度是影響橡膠材料性能的首要因素.

(3)本研究擬合的兩種高壓電纜終端應力錐橡膠材料的本構方程,在伸長率小于 200%的應變范圍內,與試驗數據可以較好地吻合.說明在此范圍可以實際反映兩種材料的本構關系,完全適用于工程實際.

(4)高壓電纜終端應力錐橡膠材料性能不穩定,還需要進一步研究其他影響因素,如老化、疲勞等.

[1] 應啟良,魏東,高小慶,等.我國高壓及超高壓交聯聚乙烯絕緣電力電纜的應用和發展[J].電線電纜,2001(3):3-9.

[2] 于景豐,趙鋒.電力電纜實用技術[M].北京:中國水利水電出版社,2003.

[3] 羅俊華,邱毓昌,楊黎明.10 kV及以上電力電纜運行故障統計分析[J].高壓電工程,2003,25(6):14-16.

[4] 王佩龍,車年堅.高壓交聯電力電纜附件選型的若干問題[J].電力設備,2004,5(8):18-22.

[5] 李新平,劉守功,曹曉瓏,等.高壓電纜終端結構設計的進展[J].電線電纜,2002(3):11-14.

[6] 李仁飛.兩種電纜附件的技術和安全性比較[J].山東電力技術,2004,137(6):78-79.

[7] 韓軒,馬永其.高壓交聯電纜終端預制橡膠應力錐的研究進展[J].絕緣材料,2007,40(4):12-17.

[8] 全國橡膠與橡膠制品標準化技術委員會橡膠通用物理試驗方法分技術委員會.GB/T 258—1998硫化橡膠或熱塑性橡膠拉伸應力應變性能的測定[S].北京:中國標準出版社,1998.

[9] MOONEY R.A theory of large elastic deformation[J].J Appl Phys,1940,11:582-592.

[10] RIVLIN R S. Large elastic deformation of isotropic materials[J].Philos Trans Roy Lond Ser A,1948,240:459-508.

[11] 劉微,金日光,勵杭泉.高分子材料時-溫等效性的研究[J].北京化工學院學報,1991,18(1):24-26.

[12] RIVLIN R S.The elasticity of rubber[J].Rubber Chem Technol,1992,65(3):51-67.

[13] GREGORY M J. The stress-strain behavior of filled rubbers at moderate strains[J].Plastics and Rubbers Materials and Applications,1979,4(4):84-88.

[14] WARD IM.固體高聚物力學性能 [M].徐懋,譯.北京:科學出版社,1988:55-100.

[15] N ICHOLSON DW,NELSON N.Finite element analysisof hyperelastic components[J].Appl Mech Rev,1998,51:303-320.

[16] 黃筑平.連續介質力學基礎 [M].北京:高等教育出版社,2003.

[17] 愛林根 A C.連續統力學 [M].程昌鈞,俞煥然,譯.北京:科學出版社,1991.

[18] 劉登祥.橡膠及橡膠制品 [M].北京:化學工業出版社,2005.

[19] 朱艷峰.橡膠材料的本構模型[J].橡膠工業,2006,53(2):119-124.

(編輯:孟慶勛)

Rubber M echan ical Proper ty of Stress Cone in Var iable Tem perature Fields

LU Zhong-ya1, MA Yong-qi1,2, XU Cao3
(1.Shanghai Institute of Applied Mathematics and Mechanics,ShanghaiUniversity,Shanghai200072,China;2.College of Sciences,Shanghai University,Shanghai200444,China;3.Shanghai Sanyuan Cable Accessories Co.,Ltd.,Shanghai201206,China)

TM 212;TN 304

A

1007-2861(2010)03-0237-05

10.3969/j.issn.1007-2861.2010.03.004

2009-02-18

馬永其 (1966～),男,副教授,博士,研究方向為柔性輸電技術及其穩定性.E-mail:yqma@mail.shu.edu.cn