Hil ber t空間中加權框架的擾動性及其應用
馬亞麗, 葉萬洲
(上海大學 理學院,上海 200444)
Hil ber t空間中加權框架的擾動性及其應用
馬亞麗, 葉萬洲
(上海大學 理學院,上海 200444)
加權框架具有良好的冗余性,從而為信號重構和圖像處理提供了非常有用的信息.借鑒對 Hibert空間中Riesz框架擾動和攝動的研究,著重討論加權框架也具有類似的擾動性結果.另外,討論了加權框架在實際信號消噪中的應用,并初步提出加權閾值消噪法的主要思想.
加權框架;Riesz框架;擾動性;閾值消噪;Hilbert空間
Abstract:Because the weighted frame possesses good redundancy,it supplies useful information for signal reconstruction and image p rocessing.Thispaper borrows ideas from the research on the Riesz frame perturbation in the Hilbert space,and in particular,discusses the top ic that a weighted frame has the similar perturbation result.Furthermore,application of weighted frames in the p ractical signal de-noising is considered,and the idea of the framed threshold de-noising isproposed.
Key words:weighted frames;Riesz frames;perturbation;threshold de-noising;Hilbert space
Hilbert空間中的框架理論概念起源于非調和Fourier級數的研究.1952年,Duffin等[1]在研究非調和 Fourier級數時正式提出框架的概念.小波分析中的框架通常是指 Hilbert空間中滿足某種特性的一列向量組成的集合.框架是正規正交基的一般推廣,是研究小波分析的一個主要工具,它在小波分析的發展中起到了非常重要的作用,廣泛應用于信號處理、數據壓縮、采樣理論、數學領域本身等許多學科.
關于框架擾動性的研究,Christensen[2-3]做了大量的工作,并給出許多有意義的結果.本研究受其啟發,對加權框架 (比一般框架具有更好的性質)做了類似討論,并給出加權框架擾動的一個簡潔形式.另外,討論了加權框架在信號消噪中的應用,并初步提出一種改進的閾值消噪法——加權閾值消噪法的主要思想.
1 基本概念
定義 1[4]可分的 Hilbert空間 H中的向量序列{fi}i∈N稱為框架,如果存在常數 A,B>0,使得任意 f∈H,有
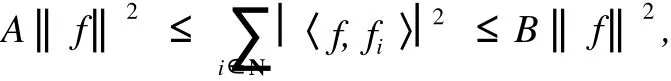
式中,A,B為框架界.若框架界 A=B,則框架{fi}i∈N稱為緊框架;若 A=B=1,則框架{fi}i∈N稱為孤立框架.最優框架界 Aopt和 Bopt分別為滿足上不等式的所有A的最大值和B的最小值.
事實上,當框架{fi}i∈N為孤立框架且‖fi‖=1時,框架{fi}i∈N即為 H的標準正交基.
注:本研究涉及到的所有的 H均為可分的Hilbert空間,N為自然數集.
定義 2[5]對序列 {wi}i∈N,如果存在常數 b≥a>0,使得對所有的 i∈N,都有 a≤wi≤b,則稱序列{wi}i∈N為半正規序列.
定義 3[5]設 F={fi}i∈N是 H中一族 ,{wi}i∈N為一正序列,稱 F={fi}i∈N為 H的加權框架,如果存在兩個常數 0 事實上,正序列 {wi}i∈N也稱作加權框架 F={fi}i∈N的嚴格正的權. 定義 4[6]序列{fi}i∈N?H稱為 Riesz基 ,如果{fi}i∈N在 H中完全且存在常數 m,M>0,使得任意數列 {ci}i∈N∈l2(N),有 滿足該不等式的最大的 m和最小的M稱為 {fi}i∈N的 Riesz基常數.若 {fi}i∈N的每個子列都是框架點列且具有一致的下界,框架 {fi}i∈N? H稱為 Riesz框架. 引理 1[7]框架與半正規序列的乘積仍為框架,即設{wi}i∈N是界為 a,b的半正規序列,如果{fi}i∈N是界為 A,B 的框架 ,則 {wifi}i∈N也為框架 ,且框架界為 a2A,b2B. 注:引理 1僅為充分不必要條件,非半正規序列與框架的乘積也可以構成加權框架,甚至有些非有界的序列亦可.雖然權序列非半正規且無界,但{wn,lφn,l}={0}∪{en}仍是框架. 引理 2[8]設{fi}i∈N是 H中的框架,則下列條件等價: (1){fi}i∈N是 Riesz框架 ; (2)存在 A>0,對任意滿足{fi}i∈N線性無關的有限集Δ?N,{fi}i∈N有下 Riesz基常數 A. 定理 1 設{wi}i∈N是界為 a,b的半正規序列,{fi}i∈N是 H中的 Riesz框架 ,則序列 {wifi}i∈N也是H中的 Riesz框架. 該定理的應用很廣泛,比如在信號重構中,如果給定的 Riesz框架不能很好的重構信號,可以通過給其適當的權值,來減小重構信號與原信號的誤差. 定理 2 設 {wi}i∈N是界為 a1,b1的半正規序列,為 H中的加權框架,且框架界為 a21A,是 H中的一個序列 ,其中 {μ}是界 定義算子 T:span{wifi}i∈N→ H,使得 顯然 T是定義好的線性算子.由文獻 [9]知,T可延拓到整個 Hilbert空間且可逆,并且有 所以 ,{μigi}i∈N是 H上的 Riesz框架. 之所以加權框架引起越來越多學者的注意,是因其比一般框架具有更好的冗余性,而框架的冗余性有助于在低精度下比較精確地重構信號,具體表現在數值穩定、誤差小等方面.在實際應用中,該冗余性所帶來的成效也是顯著的. 例 定義 CN中的標準正交基 B={b1,b2,…,bN},和一冗余度為 2的加權框架 G={g1,g2,…,g2N}={b1,b1,b2,b2,…,b2N,b2N},其中 N是自然數.下面分別用以上定義的標準正交基和加權框架來逼近被噪聲σjε污染的信號f(其中σj~N(0,1),j=1,2,…,N). 法 1 用正交基來恢復,其重構的期望誤差為 顯然,法 2的期望誤差僅是法 1的 1/2,也就是說,框架越冗余越能更好的逼近信號. 另外,我們猜想能否將加權的思想應用于小波消噪.例如,對某一有限離散含噪信號 {f(k)}k=K1k=-K1進行消噪,其中 K1以及后面的 N,M,K均為自然數.按照傳統的做法,首先,要對其進行M層小波分解,并分別記錄尺度系數 cj(j=N-1,N-2,…,N-M)和小波系數 dj(j=N-1,N-2,…,N-M);其次,選取每層閾值,并對小波系數 dj(j=N-1,N-2,…,N-M)進行閾值處理,大于閾值的系數保留,而小于閾值的系數用零替代,這樣無疑主觀地夸大了大于閾值部分噪聲信號的作用,而磨滅了低于閾值部分的有用信號在信號重構中的作用.為了彌補這一缺憾,我們試想給其加權,即通過加權,增強信號所需部分,壓制信號不需要的部分而不是完全的濾掉.由此,我們對大于閾值的系數用 mj(j=0,1,…,K)標記,并給其權ωj(j=0,1,…,K);小于閾值的系數用 nj(j=0,1,…,K)標記,并給其權ηj(j=0,1,…,K)(其中 ωj+ηj=1).再次,我們令 dj= 該研究的基本思想是容易理解的,但目前還存在一些問題.比如,該方法是否具有穩定性,即最后結果是否依賴初始值的選取,以及 Q的最優解的求解方法等,這些都是將要進一步研究的問題. [1] DUFFIN R J,SCHAEFFER A C.A class of nonharmonic fourier series[J].Trans Amer Math Soc,1952,72:341-366. [2] CHRISTENSEN O.Frame perturbation[J].Proc Amer Math Soc,1995,123(4):1217-1220. [3] CHRISTENSEN O.A Paley-Wiener theorem for frames[J].Proc Amer Math Soc,1995,123(7):2199-2201. [4] DAUBECHIES I. Ten lectures on wavelets [M].Philadelphia:SIAM,1992. [5] CHRISTENSEN O.An introduction to frames and Riesz bases[M].Boston:Birkh?user,2003. [6] 李登峰,薛明志.Banach空間上的基和框架 [M].北京:科學出版社,2007:28-164. [7] 李萬社,彭敬茹.加權框架的基本性質及與框架乘子的關系[J].云南師范大學:自然科學版,2008,28(3):1-3. [8] CASAZZA P G.Characterizing Hilbert space frameswith the subframe property[J]. Illinois JMath,1997,41:648-666. [9] CASAZZA P G, CHRISTENSEN O. Perturbation of operators and applications to frame theory[J].J Four Appl,1997,3(5):543-557. [10] 程正興.小波分析導論[M].西安:西安交通大學出版社,1998. [11] 程乾生.信號數字處理的數學原理 [M].2版.北京:石油工業出版社,1993:744-749. (編輯:孟慶勛) Per turbation of W eighted Frames in Hil ber t Space and Applications MA Ya-li, YEWan-zhou O 174.2 A 1007-2861(2010)03-0277-04 10.3969/j.issn.1007-2861.2010.03.012 2008-12-09 國家自然科學基金資助項目(60672160) 葉萬洲 (1963~),男,副教授,博士,研究方向為小波分析及其應用.E-mail:yewanzhou@eyou.com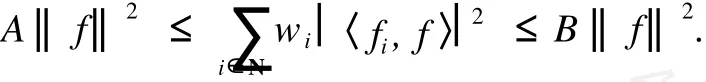
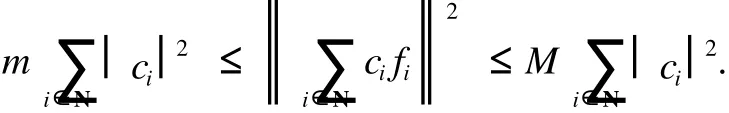
2 基本定理及引理

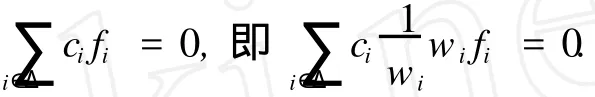
3 加權框架的擾動性結果
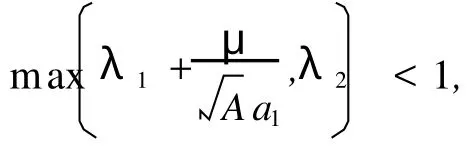


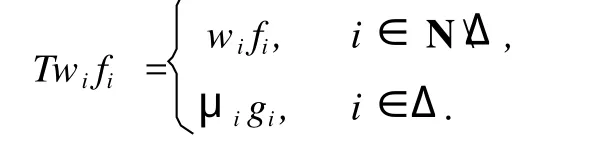
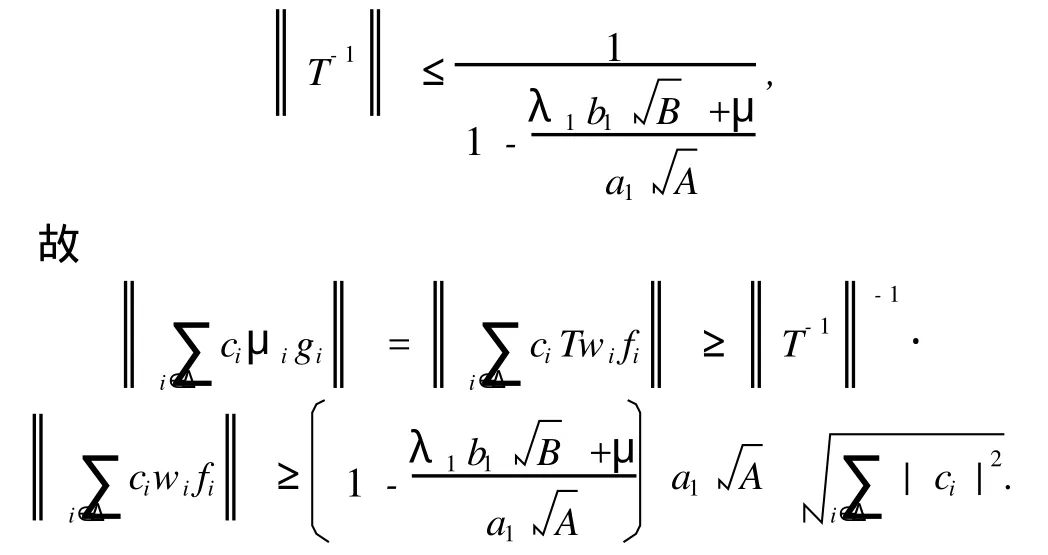
4 加權框架的應用

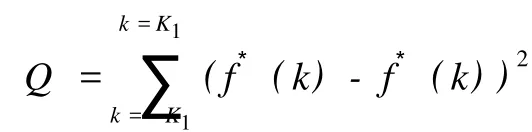
(College of Sciences,ShanghaiUniversity,Shanghai200444,China)

