具有正則圖的有限格的一些注記
孫中舉,方捷,2
(1.汕頭大學數學系,廣東汕頭515063;2.廣東技術師范學院計算機學院,廣東廣州510665)
具有正則圖的有限格的一些注記
孫中舉1,方捷1,2
(1.汕頭大學數學系,廣東汕頭515063;2.廣東技術師范學院計算機學院,廣東廣州510665)
研究了一類具有正則圖的有限格,稱之為正則圖格.證明了一個有限格是分配的正則圖格當且僅當它是布爾格,同時找出了所有1階和2階的正則圖格.特別地,證明了8-元素布爾格是最小的3階正則圖格.
正則圖;格;布爾格
0 引言
格是一類重要的有序代數,一直以來,人們用哈斯圖來表示有序集.由于哈斯圖直觀簡潔,因而被廣泛地應用到格論與有序代數的研究中,格的很多性質都可以很好地反映在哈斯圖中.傳統的研究都側重于格的代數性質,忽視了格的哈斯圖的圖的性質,目前還沒有什么文獻研究格的圖的性質.在圖論中,頂點所連的邊數稱為該頂點的度,所有頂點的度都相等的圖稱為正則圖.關于圖的詳細知識,可參看李建中等的譯著[1].本文將正則圖和有限格結合起來,研究哈斯圖是正則圖的有限格,稱之為正則圖格.
1 定義和基本性質
定義設L是一個有限格.如果L的哈斯圖是正則圖,那么稱L是一個正則圖格.如果L的哈斯圖中每個點的度都是n,那么稱L是一個n階正則圖格.
由定義可知2階布爾格是2階正則圖格,3階布爾格是3階正則圖格.
注意到哈斯圖中的邊表示的是有序集的覆蓋關系.若點a覆蓋點b,則對任意的x∈[a,b],有x=a或x=b.設L是一個n階正則圖格,對于其中任意一元素x,由定義可知x覆蓋k個點,且被n-k個點覆蓋,0≤k≤n.如圖1所示,3階布爾格L1是3階正則圖格,其中點x覆蓋兩個點y和z,且被一個最大點1覆蓋.在哈斯圖中,我們把覆蓋點a的所有點的個數稱為點a的上度,把被a覆蓋的點的個數稱為點a的下度.例如,圖1的3階布爾格中的點x的度是3,上度是1,下度是2.
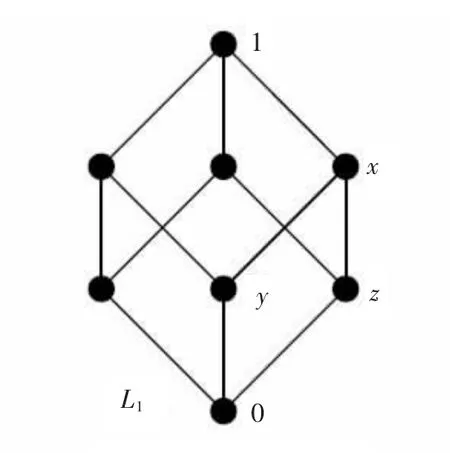
圖13 階布爾格
引理1設L1和L2是有限格.對任意的a1∈L1及a2∈L2,如果a1在L1中的度是m1,a2在L2中的度是m2,那么(a1,a2)在L1×L2中的度是m1+m2.
證明設a1在L1中被p個點覆蓋,它們是x1,x2,…,xp;a1覆蓋q個點,它們是y1,y2,…,yq;設a2在L2中被r個點覆蓋,它們是z1,z2,…,zr;a2覆蓋s個點,它們是w1,w2,…,ws.因為a1在L1中的度是m1,a2在L2中的度是m2,所以p+q=m1,r+s=m2.于是在L1×L2中,(a1,a2)被(x1,a2),(x2,a2),…,(xp,a2),(a1,z1),(a1,z2),…,(a1,zr)這p+r個點覆蓋,所以(a1,a2)在L1×L2中的上度是p+r.因為在L1×L2中,(a1,a2)覆蓋(y1,a2),(y2,a2),…,(yq,a2),(a1,w1),(a1,w2),…,(a1,ws)這q+s個點,所以(a1,a2)在L1×L2中的下度是q+s.于是(a1,a2)在L1×L2中的度是(p+r)+(q+s)=m1+m2.證畢.
定理1設L,L1,L2是有限格,而且L?L1×L2,則L是正則圖格當且僅當L1和L2都是正則圖格.
證明(?)設L1是n1階正則圖格,L2是n2階正則圖格,則由引理1可得,L1×L2中的每一點的度都是n1+n2,所以L?L1×L2是n1+n2階正則圖格.
(?)現在L?L1×L2是正則圖格.假設L1或L2不是正則圖格,不妨設L1不是正則圖格,則由正則圖格的定義知存在a,b∈L1,使得a和b的度不相等.記它們的度分別為ma和mb,則ma≠mb.設c是L2中任一元素,它在L2中的度是mc.于是由引理1可知,在L1×L2中,(a,c)的度是ma+mc,(b,c)的度是mb+mc.因為ma≠mb,所以ma+mc≠mb+mc,于是(a,c)和(b,c)的度不相等,這與L?L1×L2是正則圖格矛盾,從而推知L1和L2都是正則圖格.證畢.
推論1若L1和L2分別是n1階和n2階正則圖格,則L1×L2是n1+n2階正則圖格.
證明由引理1和定理1立即可得.
推論2設L,L1,L2,…,Ln是有限格,而且L?L1×L2×…×Ln,則L是正則圖格當且僅當L1,L2,…,Ln都是正則圖格.
2 正則圖格與布爾格
設L是一個具有最小元素0的格,a∈L,稱a是L的一個原子,若a覆蓋最小元素0.我們知道,有限的布爾格是由有限個原子所生成,由n個原子所生成的布爾格的元素個數為2n.我們將用2n表示這樣的一個n階布爾格.
定理2有限的布爾格是正則圖格.
為了后面的需要,我們給出下面引理.
引理2設L是一個有限的分配格,a是一個原子,又設b∈L.若a∧b=0,則a∨b覆蓋b.
證明首先證a∨b≠b.假若a∨b=b,則a≤b,于是a=a∧b.由于條件中a∧b=0,所以a=0,這與a是原子矛盾,所以a∨b≠b.
其次,?x∈L,如果b≤x≤a∨b,那么x=x∧(a∨b)=(x∨b)∧(a∨b)=(x∧a)∨b.因為a是原子,所以x∧a=0或x∧a=a.前者給出x=(x∧a)∨b=b,后者給出x=(x∧a)∨b=a∨b.由此推知a∨b覆蓋b.證畢.
定理3設L是一個有限格,則L是分配的正則圖格當且僅當L是布爾格.
證明由定理2,即得充分性.現證必要性.
設L是n階正則圖格,則L恰好有n個原子,記為a1,a2,…,an.設c=a1∨因為L是分配格且a1,a2,…,an是原子,所以對c.由于ai∧bi=0且ai是原子,所以由引理2可得c=ai∨bi覆蓋bi,于是c覆蓋b1,b2,…,bn.因為i≠j蘊涵ai∧bj=ai∧(ai∨…)=ai≠0,ai∧bi=0,所以i≠j蘊涵bi≠bj,于是c至少覆蓋n個不同元素b1,b2,…,bn,從而c的下度至少是n.又因為L是n階正則圖格,只有最大元1的下度不小于n,所以c=1,于是a1∨a2∨…∨an=c=1.因為a1,a2,…,an是原子,所以?x∈L,x=x∧1=x∧(a1∨a2∨…∨an)=(x∧a1)∨(x∧a2)∨…∨(x∧an)=ai1∨ai2∨…∨aik,其中i1,i2,…,in是1,2,…,n的某個排列,0≤k≤n.此時x有互補元y=aik+1∨aik+2∨…∨ain.于是L是一個有限的由原子生成的分配格,它的任一元素都有補元,所以L是布爾格.證畢.
3 低階的正則圖格
定理4我們有下面論斷:
1)1階正則圖格有且只有一個2元素格;
2)2階正則圖格是具有如圖2形式的圈.

圖22 階正則圖格
證明1)由1階正則圖格的定義立即可得.
2)設L是2階正則圖格,則L有且僅有兩個原子,這兩個原子的下度是1,上度也必須是1.L中除了最大元1和最小元0,其它元素的上度和下度都是1,所以2階正則圖格是具有上面形式的圈.證畢.
推論32階布爾格是最小的2階正則圖格.
我們知道,一個格L上所有同余關系的集合是一個完全的分配格[2],記為ConL.當L是一個有限分配格時,ConL是一個布爾格.因此,下面來自于Peter Jipsen等[2]的引理是顯然的.
引理3若L是n元素鏈,則L的同余格ConL?2n-1.
設P,Q是兩個有序集,且P有最大元α,Q有最小元β.定義P與Q的直和P⊕ˉQ如下:
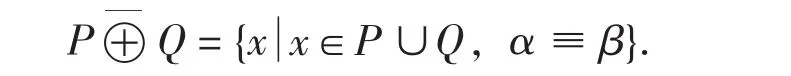
設L是一個格,又設a,b∈L且a≤b.通常用θ(a,b)表示由{a,b}生成的最小同余,稱為恒等a,b的L的主同余.文中所用相關術語與Blyth著作[3]中的相同.
稱格L的一個子格I為理想,若x≤a∈I蘊涵x∈I,記θ(I)為由I所生成的最小同余.記Ω(L)={θ(I)I是L的理想}.有如下結果.表示L中元素的個數.
證明因為L是2階正則圖格,所以由定理4可知,L有如圖3的形式.
證明因為L是2階正則圖格,所以由定理4可知L是如圖3所示的一個圈.于是L的理想I有4種可能:
1)若I={0},則θ(I)=ω(相等關系);
4)若I=L,則θ(I)=.
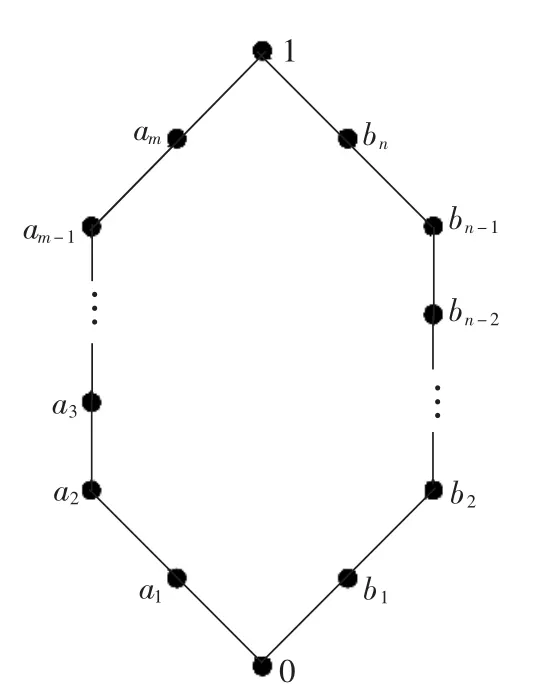
圖3 一般2階正則圖格
由定理1的推論1可知,1階正則圖格和2階正則圖格的直積是3階正則圖格,但3階正則圖格未必都是1階正則圖格和2階正則圖格的直積.圖4給出兩個3階正則圖格,其中L1是1階正則圖格和2階正則圖格的直積,而L2不可分解,故不可能是1階正則圖格和2階正則圖格的直積.
定理73階布爾格是最小的3階正則圖格.
證明設L是3階正則圖格,則其最小元0被3個元素所覆蓋,記為a,b,c.這3個元素的下度均是1,上度均是2;其最大元1覆蓋3個元素,記為x,y,z.這3個元素的上度均是1,下度均是2.于是L至少有8個元素.注意到最小元0僅被a,b,c所覆蓋及最大元1僅覆蓋x,y,z,故知由0,1,a,b,c,x,y,z所生成的L的子格為如圖5所示的3階布爾格.因而可推知,3階布爾格是最小的3階正則圖格.證畢.
關于高階的正則圖格,結果比較復雜,目前還沒有很好的結果,不過我們有如下猜想,歡迎有興趣的同行能證明此猜想.
猜想對任意正整數n,n階布爾格是最小的n階正則圖格.
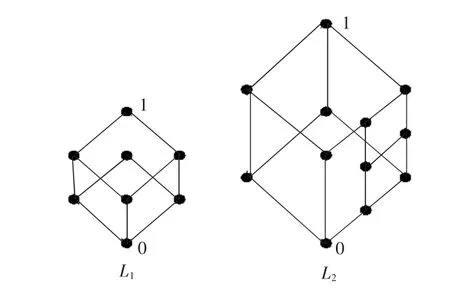
圖4 可分解和不可分解的3階正則圖格
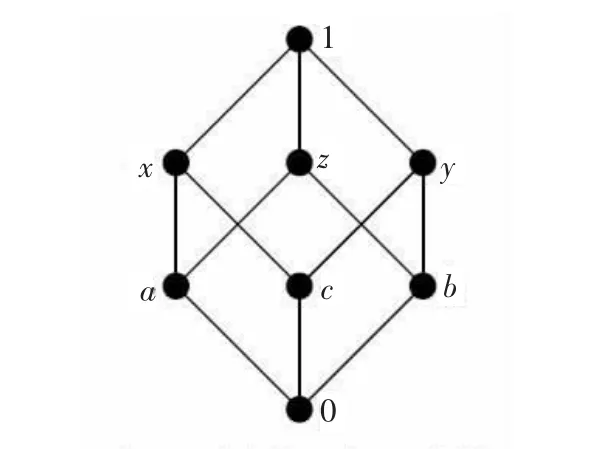
圖5 最小的3階正則圖格
[1] West D B.圖論導引[M].李建中,駱吉洲,譯.北京:機械工業出版社,2006.
[2] Jipsen P,Rose H.Varieties of latt ices[M]//Lect ure Not es in Mat hematics.Berlin:Springer Verlag Press,1992.
[3] Blyth T S,Varlet J C.Ockham algebras[M].Oxford:Oxford University Press,1994.
[4] Davey B A.On the lattice of subvariet ies[J].Houst on J Math,1979(5):183-192.
[5] Sankappanavar H P.A course in universal algebra[M].New York:Springer Verlag Press,1981.
Some Remarks on Regular Graph Lattices
SUN Zhong-ju1,FANG Jie2
(1.Department of Mathematics,Shantou University,Shantou 515063,Guangdong,China;2.School of Computer Science,Guangdong Polytechnic Normal University,Guangzhou 510665,Guangdong,China)
A regular graph lattice is a lattice whose Hass diagram is a regular graph.It is shown that a finite distributive lattice is a regular graph lattice if and only if it is a Booleanlattice.All the 1-degree graph lattices and 2-degreegraph lattices are found.It is shown that the 8-element Booleanlattice is thesmallest 3-degree regulargraph lattice.
regular graph;lattice;Boolean lattice
O 153.1;O 153.2;O 153.5
A
1001-4217(2010)02-0011-05
2009-11-03
孫中舉(1982-),男,湖北蘄春人,博士研究生.研究方向:格論與有序代數.E-mail:g_zjsun@stu.edu.cn

