一個偶數表示為兩個奇數之和的證明

陸毅

（江蘇省連云港市東海縣房山高級中學，江蘇東海222341）

一個偶數表示為兩個奇數之和的證明

陸毅

（江蘇省連云港市東海縣房山高級中學，江蘇東海222341）

一個偶數表示為兩個奇數之和有6種表達式，并且這6種表達式之間有一定的內在聯系；用數學歸納法證明了這些表達式之間的聯系.

奇數表達式；素數表達式；合數表達式；表達式的個數

0 引言

數論是許多學者研究的領域[1-4].我于2007年8月在美國《自然科學研究》上發表了題為《在偶數性質中發現一個有趣的問題》[5]的論文，東北師范大學的盛中平老師、蘇州大學的張星晨、朱東亞老師、華東師范大學的許廣龍博士、俄亥俄州大學數論博士陸三等老師都給予了高度評價，同時他們建議我有必要對該論文推導出的公式p=m+L或p=m+L+1及n=L+2m+t+2給予進一步證明［其中，p表示當偶數2n表為素數+素數與素數+合數或素數+1時的表達式個數，L表示當偶數2n表為兩個素數之和時的表達式個數，n表示當偶數2n表為兩個奇數之和時的表達式個數，2m表示當偶數2n表為素數+合數與合數+素數時的表達式個數，t表示當偶數2n表為兩個合數之和時的表達式個數，2表示兩個表達式：一個表達式是偶數2n表示為1與（2n-1）之和，另一個表達式是偶數2n表示為（2n-1）與1之和］.假如能夠證出公式L＞0（即L=n-2m-t-2＞0），其意義更大.但我一直認為此公式已經推導出來了，沒有必要去證明L＞0，因為證明L＞0是一件很容易的事情，只要精通數學的人都能證明.但他們一致認為，證明L＞0不是一件很容易的事情，并且建議我最好能給出證明.

經過5個月的思考，我終于找到證明L＞0的方法，并于2008年12月發表了題為《對“任何一個大于4的偶數都可以表示為兩個奇數之和”的思考》[6]的論文.發表不久，南京師范大學數論專家陳永高老師、上海華東師范大學數論專家韓士安老師、首都師范大學數論專家王永輝老師均提出：證明L＞0的方法是對的，但證明過程還是存在問題，必須重新修改，否則不能說明證明L＞0是一件很容易的事情.

在眾位數論專家的建議下，我經過幾個月的思考，終于找到一種證明L＞0完整、簡單而又詳細的證明過程，但這個證明過程只是我個人認為是簡單的，也許其他人還有更簡單的方法.

1 說明

在推導公式之前首先補充說明一下，在文獻［5-6］中提到的公式：p=m+L或p=m+L+1及n=L+2m+t+2，它們之間只是為了研究方便而進行的恒等變換.

在證明L＞0之前再簡單敘述一下公式p=m+L或p=m+L+1及L=n-2m-t-2的推導過程[6].設任何一個大于4的偶數為2n（n＞2，n∈N，以下相同不再重述），顯然，在偶數2n前面有n個是奇數，在這些奇數中假設有p個是素數（顯然，p中不包括素數2，因為2是偶數而不是奇數），有q個是合數（顯然，因為偶數8的前面沒有合數，所以q可以等于0），因為1既不是素數也不是合數，于是n=p+q+1.因為任何一個大于4的偶數2n都可以用它前面的每一個奇數與它前面的一個特定的奇數之和來表示，其表達式的個數是n，即偶數2n=奇數+奇數；又因為奇數還可以分為素數、合數、1，所以按照這樣的排列，偶數2n=奇數+奇數也只能有6種表達形式；當2n為小偶數時，2n表示為兩個奇數之和的表達形式可能是6種表達形式中的某幾種表達形式；當2n為充分大的偶數時，2n表示為兩個奇數之和的表達形式中一定都含有6種表達形式.這6種表達形式為：①偶數2n可能表示為1與素數之和，即偶數2n=1+素數（或偶數2n也可能表示為1與合數之和，即偶數2n=1+合數）；②偶數2n還可能表示為素數與合數之和，即偶數2n=素數+合數；③偶數2n還可能表示為兩個素數之和，即偶數2n=素數+素數；④偶數2n還可能表示為兩個合數之和，即偶數2n=合數+合數；⑤偶數2n還可能表示為合數與素數之和，即偶數2n=合數+素數；⑥偶數2n還可能表示為素數與1之和，即偶數2n=素數+1（或偶數2n也可能表示為合數與1之和，即偶數2n=合數+1）.

因為偶數2n可以用它前面的每一個奇數與它前面的一個特定的奇數之和來表示，其表達式個數為n；又因為在偶數2n前面有n個是奇數，在n個奇數中含有p個是素數，所以在n個奇數表達式（偶數2n表示為兩個奇數之和的表達形式稱為奇數表達式）中含有p個是素數表達式（偶數2n表示為一個素數與一個特定奇數之和的表達形式稱素數表達式）；在p個素數表達式中，每一個素數表達式必定有一個素數跟一個特定奇數之和，其形式也一定是下列3種表達形式中的一種：①偶數2n可能表示為素數與合數之和，即偶數2n=素數+合數；②偶數2n還可能表示為兩個素數之和，即偶數2n=素數+素數；③偶數2n還可能表示為素數與1之和，即偶數2n=素數+1.現在假設在p個素數表達式中含有L個素數表達式是兩個素數之和的表達形式，同時還假設在p個素數表達式中含有m個素數表達式是素數與合數之和的表達形式，如果2n-1是素數，那么在p個素數表達式中一定含有“偶數2n表示為素數與1之和”這個表達式，即2n=（2n-1）+1，因此，p=m+L+1；如果2n-1不是素數，那么在p個素數表達式中一定沒有“偶數2n表示為素數與1之和”這個表達式，因此，p=m+L.

同樣可以得到，在n個奇數表達式中含有q個是合數表達式（偶數2n表示為一個合數與一個特定奇數之和的表達形式稱為合數表達式）.顯然，n=p+q+1，在這里n表示當偶數2n表為奇數表達式時的表達式個數，p表示當偶數2n表為素數表達式時的表達式個數，q表示當偶數2n表為合數表達式時的表達式個數，1表示當偶數2n表示為1與（2n-1）之和時的表達式個數.例如，當偶數2n=24時，偶數24表示為奇數表達式時的表達式個數是12，即n=12，具體如下：24=1+23=3+21=5+19=7+17=9+15=11+13=13+11=15+9=17+7=19+5=21+3=23+1.偶數24表示為素數表達式時的表達式個數是8，即p=8，具體如下：24=3+21=5+19=7+17=11+13=13+11=17+7=19+5=23+1.偶數24表示為合數表達式時的表達式個數是3，即q=3，具體如下：24=9+15=15+9=21+3.偶數24表示為1+23時的表達式個數是1.在q個合數表達式中，每一個合數表達式必定含有一個合數與一個特定奇數之和，其表達式的形式也一定是下列3種表達式中的一種：①偶數2n可能表示為兩個合數之和，即偶數2n=合數+合數；②偶數2n還可能表示為合數與素數之和，即偶數2n=合數+素數；③偶數2n還可能表示為合數與1之和，即偶數2n=合數+1.同樣可以假設在q個合數表達式中含有t個合數表達式是兩個合數之和的表達形式.顯然，在q個合數表達式中也含有m個合數表達式是合數與素數之和的表達形式（因為素數+合數表示素數表達式與合數+素數表示合數表達式，只是順序和名稱不一樣，其實質是一樣的，因此有m個是素數+合數的素數表達式，同樣也就有m個是合數+素數的合數表達式.例如，12=3+9=9+3，其中3+9是表示一個素數表達式，是素數與合數之和的表達形式；9+3是表示一個合數表達式，是合數與素數之和的表達形式）.如果2n-1是合數，那么在q個合數表達式中一定含有“偶數2n表示為合數與1之和”這個表達式，即2n=（2n-1）+1，因此，q=m+t+1；如果2n-1不是合數，當然在q個合數表達式中一定沒有“偶數2n表示為合數與1之和”這個表達式，因此，q=m+t.

因為p=m+L或p=m+L+1，q=m+t或q=m+t+1，又因為2n-1要么是一個素數，要么是一個合數，只能是其中的一種（注意，2n-1＞1），所以，n=p+q+1=m+t+m+L+2，即n=L+2m+t+2，它又可以變形為L=n-2m-t-2，其中，n表示當偶數2n表為兩個奇數之和時的表達式個數，L表示當偶數2n表為兩個素數之和時的表達式個數，2m表示當偶數2n表為素數+合數與合數+素數時的表達式個數，t表示當偶數2n表為兩個合數之和時的表達式個數，2表示兩個表達式，一個表達式是偶數2n表示為1與（2n-1）之和，另一個表達式是偶數2n表示為（2n-1）與1之和.

我們再簡單說一下證明L＞0的原因，因為在數學中經常碰到很多個偶數不僅可以表示為兩個素數之和，而且它們表示為兩個素數之和的表達式個數并不唯一.例如，10=3+7=5+5，14=3+11=7+7，16=3+13=5+11，18=5+13=7+11，20=3+17=7+13，22=3+19=5+17=11+11，24=5+19=7+17=11+13，26=3+23=7+19=13+13，28=5+23=11+17，30=7+23=11+19=13+17，32=3+29=13+19，34=3+31=5+29=11+23=17+17，36=5+31=7+29=13+23=17+19，38=7+31=19+19，40=3+37=11+29=17+23，…….這些例子在數學中是比較簡單、常見的，卻一直沒有引起人們的關注和思考.往往簡單的問題都隱藏著絕妙的玄機.上面的那些例子暗示我們去思考：一個大于4的偶數2n表示為兩個素數之和的表達式個數到底有多少，跟什么有關？像這樣的偶數有多少，又有什么規律？如何去尋找？是不是每一個大于4的偶數2n都可以表示為兩個素數之和呢？我按照這個思路，先從偶數6開始尋找，一直到偶數6 002，書寫了幾百萬個數學式子，終于發現：偶數2n表示為兩個素數之和的表達式個數，隨著該偶數2n的增大而成波動性增加，即L值在增加過程中有少數是相對降低的，但總的趨勢是增加的.這個結論只是從一部分事例中獲得，而哥德巴赫猜想只是它（L=n-2m-t-2）的一部分，想利用這個結論為哥德巴赫猜想的研究開辟新的途徑，就必須從理論上證明L＞0.我們現在根據公式L=p-m或L=p-m-1（即L=n-2m-t-2），再從理論上來研究：在n個奇數表達式中含有兩個素數之和的表達式個數L.

2 證明過程

根據題意，L只能是非負整數，只要證明L＞0，就可以充分說明：每一個大于4的偶數2n都可以表示為兩個奇素數之和，而證明公式L=p-m或L=p-m-1，利用數學歸納法即可證出，具體證明過程如下.

當m=0時：

當偶數2n=4時，4表示為兩個奇數之和的表達式有2個，即4=1+3=3+1，4不能表示為素數+合數的表達形式，則p=m+L+1（p=1，即4=3+1）、m=0，L=pm-1=1-0-1=0，L=0說明當p=1時，偶數4不能表示為兩個奇素數之和，顯然這個結論也符合實際；

當偶數2n=6時，6表示為兩個奇數之和的表達式有3個，即6=1+5=3+3=5+1，6不能表示為素數+合數的表達形式，則p=m+L+1（p=2，即6=3+3=5+1）、m=0，L=p-m-1=2-0-1=1＞0；

當偶數2n=8時，8表示為兩個奇數之和的表達式有4個，即8=1+7=3+5=5+3=7+1，8不能表示為素數+合數的表達形式，則p=m+L+1（p=3，即8=3+5=5+3=7+1）、m=0，L=p-m-1=3-0-1=2＞0；

當偶數2n=10時，10表示為兩個奇數之和的表達式有5個，即10=1+9=3+7=5+5=7+3=9+1，10不能表示為素數+合數的表達形式，則p=m+L（p=3，即10=3+7=5+5=7+3）、m=0，L=p-m=3-0=3＞0.

討論到這里有的朋友可能會問：m=0除了偶數4、6、8、10以外，是否存在更多的偶數呢？這個很可能有，但是我們不需要找出所有的偶數，并且尋找也很困難，因為隨著偶數的增大，該偶數表示為素數表達式p也在增大，而m不變還等于零，所以L顯然大于零.顯然下文m=1也是這樣.

當m=1時：

當偶數2n=12時，12表示為兩個奇數之和的表達式有6個，即12=1+11=3+9=5+7=7+5=9+3=11+1，12表示為素數+合數的表達式有1個，即12=3+9，則p=m+L+1（p=4，即12=3+9=5+7=7+5=11+1）、m=1，L=p-m-1=4-1-1=2＞0；

當偶數2n=14時，14表示為兩個奇數之和的表達式有7個，即14=1+13=3+11=5+9=7+7=9+5=11+3=13+1，14表示為素數+合數的表達式有1個，即14=5+9，則p=m+L+1（p=5，即1 4=3+1 1=5+9=7+7=1 1+3=1 3+1）、m=1，L=pm-1=5-1-1=3＞0；

當偶數2 n=1 6時，1 6表示為兩個奇數之和的表達式有8個，即1 6=1+1 5=3+1 3=5+1 1=7+9=9+7=1 1+5=1 3+3=1 5+1，1 6表示為素數+合數的表達式有1個，即1 6=7+9，則p=m+L（p=5，即1 6=3+1 3=5+1 1=7+9=1 1+5=1 3+3）、m=1，L=p-m=5-1=4＞0；

當偶數2 n=1 8時，1 8表示為兩個奇數之和的表達式有9個，即1 8=1+1 7=3+1 5=5+1 3=7+1 1=9+9=1 1+7=1 3+5=1 5+3=1 7+1，1 8表示為素數+合數的表達式有1個，即1 8=3+1 5，則p=m+L+1（p=6，即1 8=3+1 5=5+1 3=7+1 1=1 1+7=1 3+5=1 7+1）、m=1，L=p-m-1=6-1-1=4＞0；

當偶數2 n=2 4時，2 4表示為兩個奇數之和的表達式有1 2個，即2 4=1+2 3=3+2 1=5+1 9=7+1 7=9+1 5=1 1+1 3=1 3+1 1=1 5+9=1 7+7=1 9+5=2 1+3=2 3+1，2 4表示為素數+合數的表達式有1個，即2 4=3+2 1，則p=m+L+1（p=8，即2 4=3+2 1=5+1 9=7+1 7=1 1+1 3=1 3+1 1=1 7+7=1 9+5=2 3+1）、m=1，L=p-m-1=8-1-1=6＞0.

在這里我們為什么不討論偶數2 n=2 0、2 2，而直接討論偶數2 n=2 4？因為2 0表示為兩個奇數之和的表達式有1 0個，即2 0=3+1 7=5+1 5=7+1 3=1 1+9=1 3+7=1 7+3=1 9+1，2 0表示為素數+合數的表達式有2個，即2 0=5+1 5=9+1 1，所以m=2；同樣可以得到，在偶數2 n=2 2中m=2，而這里專門討論m=1，因此我們不討論偶數2 n=2 0、2 2.

假設當m=k時，L1=p1-k＞0或L1=p1-k-1＞0（注意，通過上面討論我們還可以發現，每一個m值可以對應多個L、p值，事實上也是這樣，所以，當m=k時，L1、p1也不是對應一個L、p值，而是代表在m=k時所有L、p值.下文中L2、p2的意思也是如此）.則當m=k+1時，可設L2=p2-（k+1）或L2=p2-（k+1）-1.因為p=m+L或p=m+L+1，所以當m由k變為k+1時，p值存在3種變化情況.

1）p值增加.顯然L2=p2-（k+1）＞0或L2=p2-（k+1）-1＞0.

2）p值減少.因為p=m+L或p=m+L+1，所以p值減少，L就減少，因為p1=k+L1或p1=k+L1+1，p2=k+1+L2或p2=k+1+L2+1，所以p1-p2=L1-L2，或p1-p2=L1-L2-1，或p1-p2=L1-L2-2；又因為p1=k+L1或p1=k+L1+1，p2=k+1+L2或p2=k+1+L2+1，所以p1-L1=p2-L2，或p1-L1=p2-L2-1，或p1-L1=p2-L2-2；再將式p1-p2=L1-L2、p1-p2=L1-L2-1、p1-p2=L1-L2-2的兩邊分別同時乘以等式p1-L1=p2-L2、p1-L1=p2-L2-1、p1-L1=p2-L2-2的兩邊，得到等式：①（p1-p2）（p1-L1）=（L1-L2）（p2-L2），或②（p1-p2）（p1-L1）=（L1-L2）（p2-L2-1），或③（p1-p2）（p1-L1）=（L1-L2）（p2-L2-2），或④（p1-p2）（p1-L1）=（L1-L2-1）（p2-L2），或⑤（p1-p2）（p1-L1）=（L1-L2-1）（p2-L2-1），或⑥（p1-p2）（p1-L1）=（L1-L2-1）（p2-L2-2），或⑦（p1-p2）（p1-L1）=（L1-L2-2）（p2-L2），或⑧（p1-p2）（p1-L1）=（L1-L2-2）（p2-L2-1），或⑨（p1-p2）（p1-L1）=（L1-L2-2）（p2-L2-2）.為了研究方便，將①化簡整理得到：-L2（p2+L1）--p1p2-p1L1）=0，解之得：顯然，L2＞0.同理可證，其它等式中的L2＞0.所以當m由k變為k+1、p值減少時，L2=p2-（k+1）＞0或L2=p2-（k+1）-1＞0.

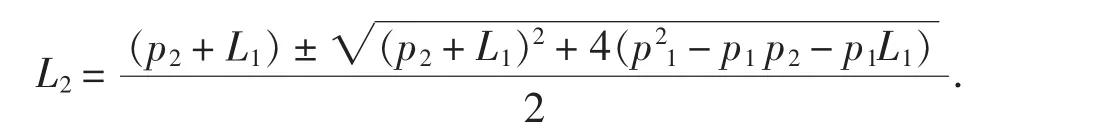
3）p值不變.因為p值不變，所以p1=k+L1或p1=k+L1+1，p2=k+1+L2或p2=k+1+L2+1，所以，①p-L1=p-L2，或②p-L1=p-L2-1，或③p-L1=p-L2-2.再將①、②、③等式兩邊平方得到：④（p-L1）2=（p-L2）2，或⑤（p-L1）2=（p-L2-1）2，或⑥（p-L1）2=（p-L2-2）2.為了研究方便，將④化簡整理得到：L22-2pL2+2pL1-L12=0，解之得：顯然，L2＞0.同理可證，其它等式中的L2＞0.因為①、②、③等式兩邊均是非負數，所以通過平方后得到的④、⑤、⑥式子中L2的范圍沒有變化，所以當m由k變為k+1、p值不變時，L2=p2-（k+1）＞0或L2=p2-（k+1）-1＞0.所以當m=k+1時，L2=p2-（k+1）＞0或L2=p2-（k+1）-1＞0.

所以當m≥0，m∈N時，公式L=p-m＞0或L=p-m-1＞0.由于L=n-2mt-2是由L=p-m或L=p-m-1推導而來，所以當n＞2，n∈N時，公式L=n-2m-t-2＞0，其中，p表示當偶數2n表為素數+素數與素數+合數或素數+1時的表達式個數（注意，在公式L=p-m中，p不包括表達式：素數+1），L表示當偶數2n表為兩個素數之和時的表達式個數，n表示當偶數2n表為兩個奇數之和時的表達式個數，t表示當偶數2n表為兩個合數之和時的表達式個數，m表示當偶數2n表為素數+合數時的表達式個數，2m表示當偶數2n表為素數+合數及合數+素數時的表達式個數，那么公式p-m-1中最后一項1就是表示當（2n-1）是素數時，偶數2n表示為（2n-1）+1，公式L=n-2m-t-2中最后一項2就表示偶數2n表示為（2n-1）+1與1+（2n-1）.

[3] 陳景潤.陳氏定理（1+2）的證明[C].北京：清華大學出版社，1973.

[5] Lu Yi.An interesting problem discovered in the properties of even numbers[J].Natural Science Research，2007，12（4）：93-95.

[6] 陸毅.對“任何一個大于4的偶數都可以表示為兩個奇數之和”的思考[J].山西師范大學學報（自然科學版）研究生專刊，2008（22）：3-6.

A Proof of Representing of an Even Number as Summation of Two Odd Numbers

LU Yi

(Fangshan High school，Tonghai，Lianyungang 222341，Jiangsu，China)

An even number is represented as a summation of two odd numbers in 6 expressions.The relationship among the expressions are demonstrated and proved with mathematical induction.

odd number expression；prime number expression；summation；number of expressions

O 156.4

A

1001-4217（2010）01-0001-07

2009-10-09

陸毅（1967-），男，江蘇連云港人，本科.研究方向：解析數論-哥德巴赫猜想.E-mail：luyi1967314@163.com