基于動態MAUT的油氣勘探風險決策模型研究

王 眾，張哨楠，匡建超

（成都理工大學能源學院油氣藏地質及開發工程國家重點實驗室，四川 成都610059）

油氣勘探屬于典型的 “三高一長” （高投入，高風險，高產出，長周期）項目，作為石油公司的一項主要投資活動，勘探項目的風險決策一直是倍受關注的研究領域。如何從效益-風險的角度，對勘探目標進行科學決策，降低風險、提高經濟效益，已成為我國油氣工業發展面臨的瓶頸問題。然而，傳統決策方法往往以期望收益最大化為決策準則，忽視了決策者的風險承受能力和風險偏好。隨著以風險偏好為核心的現代效用理論的提出，風險決策準則逐漸發展為期望效用最大化。[1，2]20世紀70年代，Keeney提出的多屬性效用理論 （MAUT），又將效用決策由單屬性發展為多屬性，較好地解決了多目標決策問題。20世紀90年代以來，以Walls和Suslick為代表的學者，又將MAUT引入油氣領域，均取得了不錯效果。[3]

筆者以Suslick提出的MAUT決策框架為基礎，從風險-收益的角度出發，凝練出 “地質風險”、“市場風險”和 “經濟收益”3大屬性，并設定屬性權重的變化范圍，對屬性進行動態賦權，構建了基于動態MAUT的勘探風險決策模型。該方法不僅充分考慮了決策者的風險偏好，且能夠反映決策結果的穩定性，幫助決策者以動態、全面的眼光進行風險決策分析，從而使得決策過程更加科學，結果更加合理。

1 多屬性效用理論 （MAUT）

多屬性效用理論 （Multi-Attribute Utility Theory，MAUT）是一種結構化、邏輯化、系統化的決策分析理論。通過多屬性效用函數，將決策者對待風險的態度、經驗及判斷能力等主觀因素與方案的客觀損益有機結合在一起，以效用的期望值作為決策依據。MAUT基本原理，就是首先通過效用的分解，得到一系列與目標相關的單一屬性；然后計算單一屬性的效用值及其權重；再根據各屬性之間的相關性選擇適當的模式，再對其進行組合，得到反映決策者偏好的多屬性效用函數；最終，根據總效用值的大小進行方案優選。

2 基于動態MAUT的油氣勘探決策模型

（1）屬性的確定及效用函數生成

油氣勘探屬于典型的高風險、高收益項目。筆者在總結前人研究的基礎上，充分考慮勘探項目的風險與收益，以 “地質風險”、 “市場風險”和 “經濟收益”作為決策模型的三大屬性。對于“地質風險”，筆者以地質成功概率為評估標準，成功概率越大，效用值越大；對于 “市場風險”，以凈現值標準差為評估標準，標注差越大，屬性越小；對于 “經濟收益”，以最大期望投資收益率為評估標準，期望收益率越大，屬性值越大。

（2）多屬性效用函數的確定

設方案集A= ｛A1，A2，A3，…，Am｝，各方案多屬性效用函數為Uj（X），j=1，2，…，m。一般而言，將單屬性效用復合為多屬性效用，可以分為加法模式和相乘模式兩種：

① 若屬性之間相互獨立，使用加法模式：

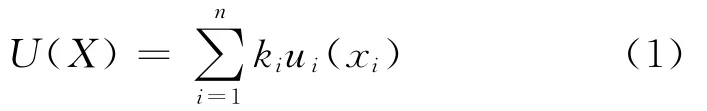
式中：ki—第i個屬性的權重，且1。

② 若屬性之間存在相關性，使用相乘模式：

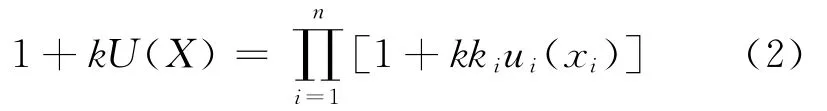
式中：ki——第i個屬性的權重 （0≤ki≤1），且；k為常數，且有

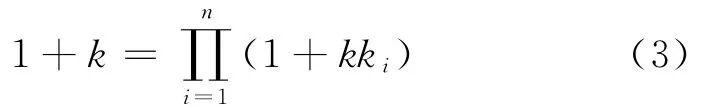
（3）屬性權重的確定

屬性權重的確定，一直是MAUT在實際應用中的一個難點。傳統賦權方法，一般分為靜態專家賦權和動態隨機賦權兩大類。然而，筆者認為，這兩種方法各有優缺點：靜態專家賦權，雖考慮了專家經驗，但難以取得統一、精確的結果；動態隨機賦權，雖然能對決策結果的穩定性進行檢驗，但某些隨機確定的權重值，明顯超出了合理范圍，缺乏科學性。基于此，本文在動態賦權的基礎上，融入專家經驗，設定各屬性權重的分布形式和變化范圍，在此范圍內進行動態賦權。該方法不僅充分考慮了專家經驗，同時也能夠反映權重變化對決策結果的影響，有利于決策者以全面、動態的眼光做出科學的決策。

（4）最優方案的確定

首先考慮屬性之間相互獨立的情況，若仿真n次，共得到p組總效用集 ｛U1（X），U2（X），…，Um（X）｝1，…… ，｛U1（X），U2（X），…，Um（X）｝p。將每一組效用集中的方案，按照效用值大小排序，這樣將得到p種排序情況：若方案j排第一、第二，……、第m的次數分別為t1，t2，則方案Aj為最優方案、優方案、……、最差方案的概率分別為t1/p，t2/p，…，tm/p；同理，可求出其余方案的排序概率，并將這些概率描繪到圖上，便于觀察各方案排序由于屬性權重不同而變化的情況。類似的，再考慮屬性間相關的情況。最后，綜合考慮獨立和相關兩種情況，選擇最優方案。

3 應用實例

為了檢驗模型的實際應用效果，筆者以文獻[9]的數據為基礎，挑選出 “地質成功概率大于0.6”且 “最大預期現金流大于15億元”的5個勘探項目組成備選方案集，運用動態MAUT風險決策模型對其進行決策分析。決策的結果合理，符合客觀實際。

（1）構造效用函數。通過對某油氣勘探開發公司決策人員的風險偏好問卷調查 （具體過程請參見文獻 [2]），確定了決策者對于屬性集X=｛地質儲量、經濟效益、技術風險｝中各屬性的3個效用確定當量點，并根據公式

式中，a、b—常數，c—風險厭惡因子。該效用函數的確定取決于式 （4）中的3個待定參數a、b和c。通過確定函數的3個確定當量點，即效用最大點 （u=1）、效用最小點 （u=0）以及中位值點（u=0.5），聯立3個方程，便求出唯一的效用函數表達式。得出各屬性的效用函數表達式，結果見表1。

表1 各屬性的效用確定當量點

（2）計算各方案的單個屬性效用值。根據表1中求出的各屬性效用函數，計算各勘探項目各單一屬性的效用值，計算結果見表2。

（3）確定各屬性權重的分布規律和變化范圍。文本請專家對屬性進行賦權，綜合專家意見，得出各個屬性權重的分布規律和變化范圍見表3。

（4）計算各方案的總效用，挑選最優方案。筆者運用Matlab進行相應的程序設計，考慮屬性獨立和相關兩種狀態，分別仿真10000次，得出各方案的排序情況，見圖1和圖2。

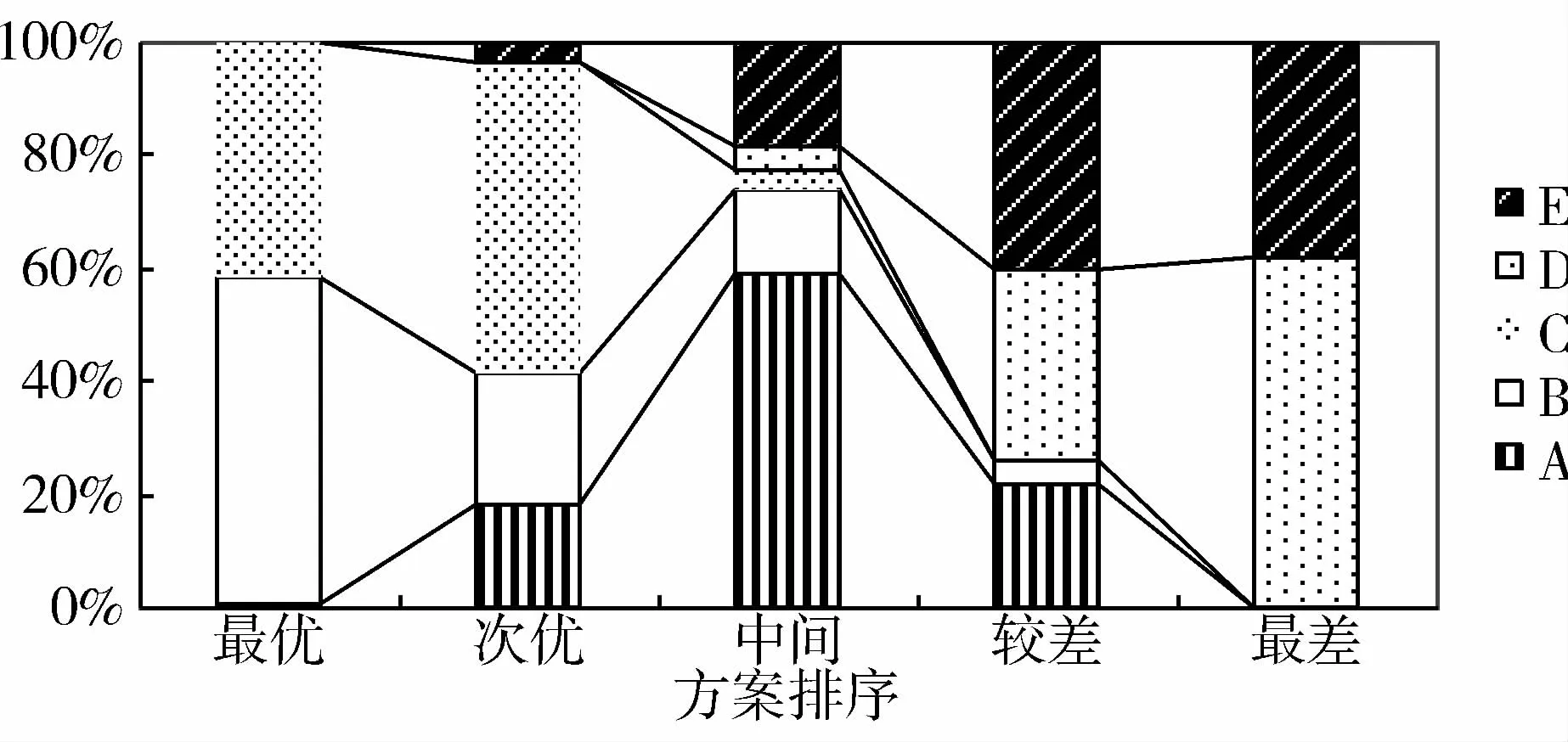
圖1 屬性獨立的方案排序圖

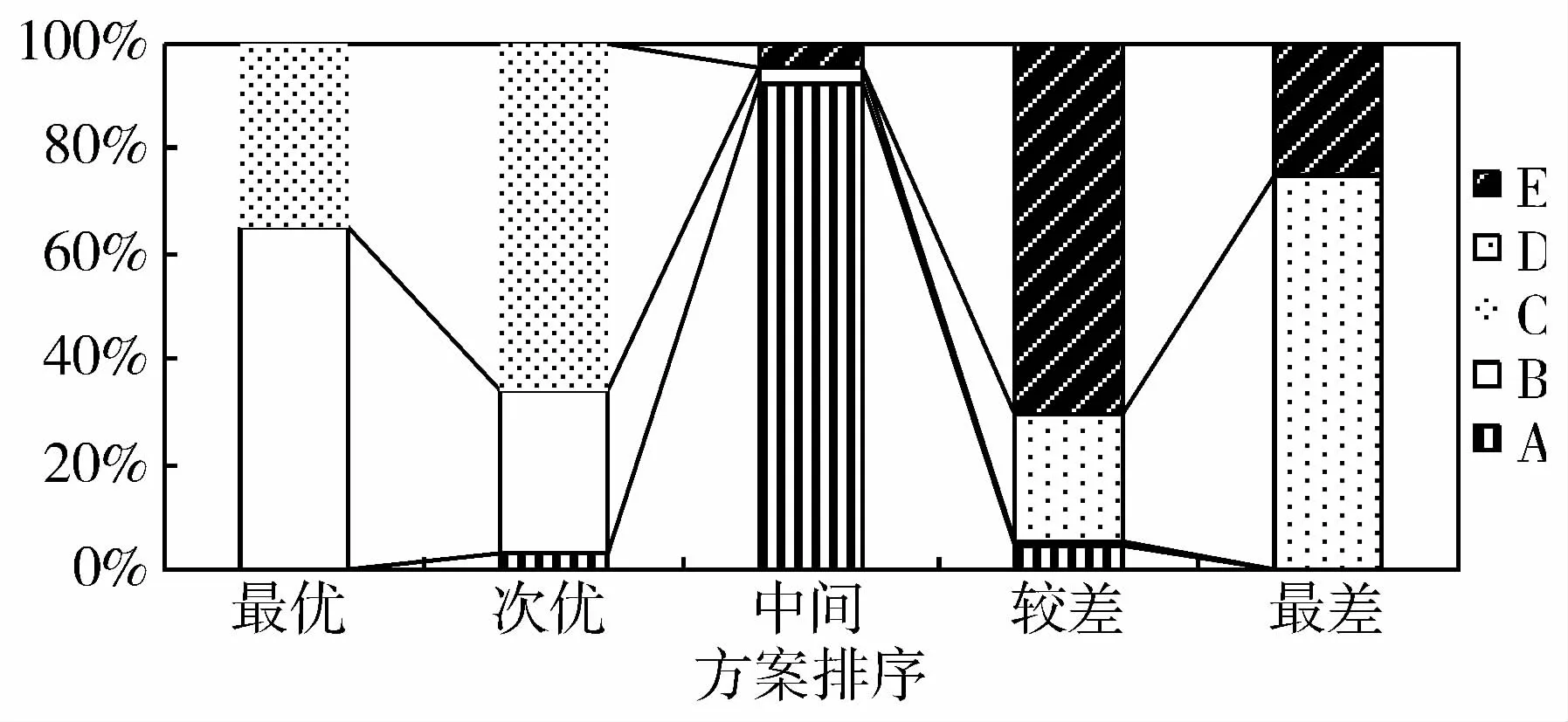
圖2 屬性相關的方案排序圖

由圖1、圖2，可以很清晰的觀察由于屬性權重變化而導致各個方案排序變化的情況。根據圖1分析：B作為最優方案的概率最大 （57%），但不穩定，受到屬性權重變化的影響較大，有大約15%和4%的可能成為中間和較差方案；C為最優方案的概率略低于B（42%），但作為次優方案的概率最高，同時穩定性較高 （為中間方案的概率小于4%，為較差和最差方案的概率為0）。根據圖2分析：B依然作為最佳選擇，其概率更是高達65%，同時穩定性大大提高；C作為最優方案的概率雖然有所下降，但為次優方案的累積概率已經高達99.9%。

綜合考慮圖1、圖2，筆者認為，若決策者認為B方案排序的波動在承受范圍內，則B為最優方案，C為次優方案；若決策者對穩定性要求較高，則C為勘探投資的最優方案。

4 結語

油氣勘探的風險決策是一個系統、復雜的決策過程。多屬性效用理論 （MAUT）借助效用函數來表示各屬性對備選方案的貢獻，有助于決策者考慮、分析油氣勘探過程中涉及的相關因素以及決策者的風險偏好。此外，結合動態賦權，使得決策者能夠了解各個方案受屬性權重變化的影響，幫助決策者以全面動態的眼光來進行決策分析。應用實例結果表明，基于動態MAUT的決策模型，能夠有效地幫助決策者對于油氣勘探項目，做出科學、合理的決策。