基于結構可靠度的在役橋梁剩余價值分析研究

陳 莘

(安徽省公路橋梁工程公司,安徽合肥 230031)

基于結構可靠度的在役橋梁剩余價值分析研究

陳 莘

(安徽省公路橋梁工程公司,安徽合肥 230031)

對在役橋梁進行剩余價值分析,對于路政部門加強橋梁維護維修、加固甚至新建等決策管理都有實際意義。基于可靠度理論提出了一種折舊方法并用其進行剩余價值計算,為公共項目建設宏觀經濟的成本分析提供一種量化的工具。

橋梁工程;維護維修與加固;管理

0 引言

在進行橋梁改造升級與新建橋梁之間的方案比選和經濟決策時,需要考慮現有的在役橋梁的剩余價值問題,此時,用會計學方法來做宏觀經濟分析顯然不合適[1]。在役橋梁實際運營過程中,由于各種因素的影響,橋梁的使用壽命存在不確定性,本文試圖提出基于橋梁可靠度的方法來探討在役橋梁的剩余價值。

安全性、適用性和耐久性總稱為結構的可靠度。目前,國際上對結構可靠度的一致定義為:結構在規定的時間內,在規定的條件下,完成預定功能的概率[2]。結構可靠度的提出就是為了使結構在安全適用和經濟合理之間選擇一種合理的平衡,本身就是一種基于技術可行性和經濟合理性的產物,是技術和經濟結合的一個指標。大連理工大學的趙國藩等人在舊有結構性能評估[3]和結構全過程可靠度[4]研究中取得了大量成果,從而使我們在判定在役橋梁的結構狀態時有了相應依據。根據當時狀態而判斷其剩余價值,在理論上和操作上應該具有相當的可行性。

1 在役橋梁資產折舊計算參數的確定

1.1 折舊的基數

計算固定資產折舊的基數一般為取得固定資產的原始成本,即固定資產的賬面原值。本文所討論的在役橋梁賬面原值指的是從立項、設計、施工階段構成固定資產的資金投入。

1.2 固定資產的凈殘值

固定資產的凈殘值是指預計的固定資產報廢時可以收回的殘余價值扣除預計清理費用后的數額。和其他一般的固定資產不同,橋梁工程到了使用末期可能存在負的凈殘值,即為數不菲的拆橋費用。

1.3 固定資產的使用年限

固定資產的使用年限是指固定資產預計的經濟使用年限。在確定固定資產使用年限時,不僅要考慮固定資產的有形損耗,還要考慮固定資產的無形損耗。我國目前處在經濟大發展時期,交通基礎措施的建設處于滯后階段,一般可以認為在役橋梁的經濟壽命為其自然壽命。

2 基于結構可靠度的在役橋梁剩余價值分析方法

2.1 橋梁的可靠度理論模型

一般認為結構的恒載效應服從正態分布,其統計參數可以通過實測得到。己有結構的可變荷載效應是一個與剩余使用壽命期有關的量,可以根據結構在已服役期內的荷載實測資料進行統計分析。如果沒有足夠的實測資料,可以按設計時荷載的統計特性進行推算。結構上的可變荷載效應服從極值I型分布,時段t內可變荷載效應的平均值μSQt,標準差σSQt可以表示為:式中:TS為規范給定的結構設計使用期;μSQT和σSQT分別為設計使用期內荷載效應極大值的平均值和標準差。

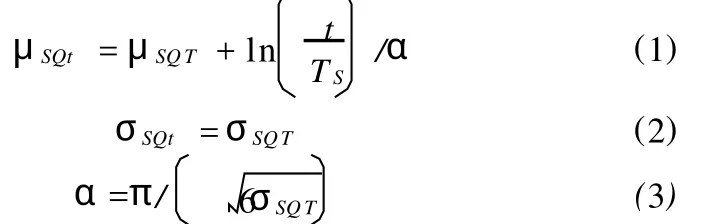
己有結構是一個客觀存在的實體,其抗力理論上可視為一確定量,但是由于各種因素的影響以及檢測手段的限制,測量時存在一定的誤差,因此仍具有一定的隨機性,抗力隨時間變化的模型可以用一個簡單的隨機過程模型表示為:

式中:R(t)為結構在t時刻的抗力;F(t)為結構抗力衰減—時間函數(與結構的組成材料、環境以及維護條件有關)。

第ti時刻的功能函數為:

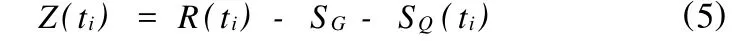
式中:R(ti)為結構ti時刻結構抗力;SQ(ti)為ti時刻可變荷載效應;SG為恒載效應。在時段[0,t]內結構的失效概率可以表示為:

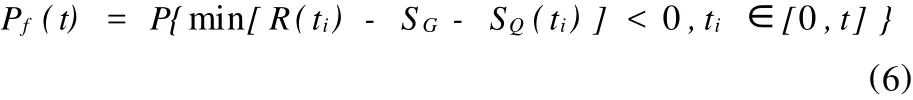
相應的可靠指標為:

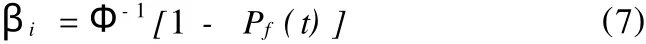
βi為[0,t]時段內的可靠指標;Φ-1(·)為正態分布函數的逆函數。

2.2 基于可靠度的在役橋梁剩余價值

一般的折舊方法,以平均年限法為例,固定資產在某一時刻的剩余價值計算公式如下:

年折舊率=[(1一預計凈殘值率)/折舊年限]×100%

年折舊額=固定資產賬面原值×年折舊率固定資產剩余價值=固定資產賬面原值—∑年折舊額

根據這種思路,考慮以結構的失效概率作為其折舊率,其可靠度為目前的剩余價值比率,那么,對處在ti時刻的在役橋梁,其剩余價值計算流程為:

(1)對在役橋梁的性能進行評估,得到當前狀態的可靠度指標。

(2)用可靠度指標與經濟參數相乘,得到在役橋梁的剩余價值。

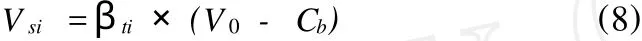
式中:Vsi為當前橋梁的剩余價值;βti為當前狀態的可靠度指標;V0為橋梁折舊的計算基數,即橋梁的初始價值;Cb為橋梁拆除的花費(凈值)。

3 在役橋梁剩余價值計算方法的修正

式(8)有一個明顯的問題,就是沒有考慮資金的時間價值。要考慮資金運動中的增值,就必須對該公式進行修正。

3.1 理論上的在役橋梁剩余價值的計算公式

在考慮資金時間價值的情況下,理論上的在役橋梁剩余價值的計算公式為:

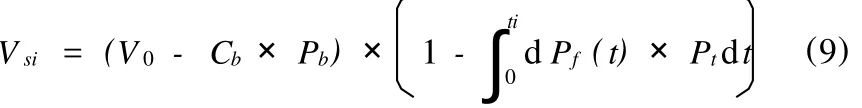
式中:dPf(t)為失效概率的增量微元;Pt為t時刻的資金折現系數;Pb為拆除時的資金折現系數。

對于式(9),dPt(t)與Pt的確定是比較難的。但可通過離散的方法將之轉化解決。

3.2 離散化的解決辦法

文獻[4]中將設計基準期分成m個相等的時段,將荷載隨機過程離散成m個隨機變量SQ(ti),將抗力隨機過程離散成m個隨機變量R(ti),R(ti)的大小取第i個時段抗力的中值,推導出了考慮抗力變化的結構可靠度的實用計算方法,同時指出,若可變荷載的極大值分布服從極值I型分布時,結構在[0,t]時段內的失效概率為:

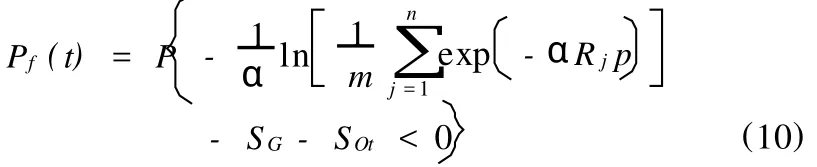
式中:α為極值I分布的參數;m為將[0,t]分隔成的時段數;Rj為第j個時段結構抗力效應的中值;SQt為[0,t]時段內可變荷載效應的極大值。

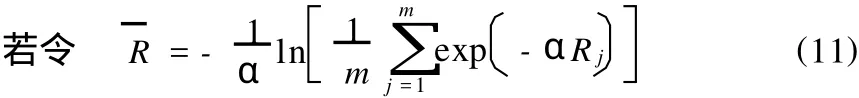
可將R視為結構的等效抗力,反應的是結構抗力的退化過程。

結構在某一時段[ti,ti+δt]內的失效概率增加量為:

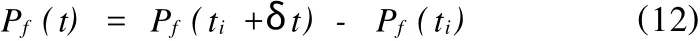
對于某一個確定的時間點,資金的折現系數也容易根據相關表格得到。那么此時的計算公式應該為: 3.3 離散化處理后橋梁剩余價值計算流程

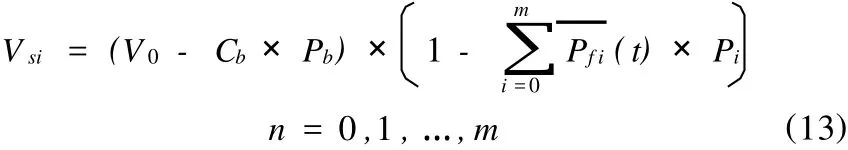
計算結構某一時段的在役橋梁剩余價值的計算步驟如下:

(1)描述結構所處的環境及材料特性,建立結構抗力衰減模型。

(2)實測當前狀態下結構抗力和荷載的統計參數。

(3)把設計基準期離散化,根據式(6)計算各個時段的失效概率Pfi(t)。

(4)根據公式(12)計算各個時段的失效概率增加量Pfi。

(5)根據折現系數表和相應的參數(折現率、時段長)查出折現各Pfi(t)時對應的Pi。

(6)根據式(13)計算現階段橋梁剩余價值Vsi。

4 算例分析

某大橋位于國道101線,橋梁上部構造為裝配式鋼筋砼無中橫隔梁T形梁橋,混凝土標號為C25,內梁采用火山灰水泥,外梁采用普通水泥。下部為雙柱墩,基礎有2種型式:鉆孔樁基礎與淺基礎。利用實際檢測數據建立鋼筋銹蝕和混凝土強度時變模型,對鋼筋混凝土梁橋抗彎承載力進行計算,得出如圖1所示的抗力時變規律。

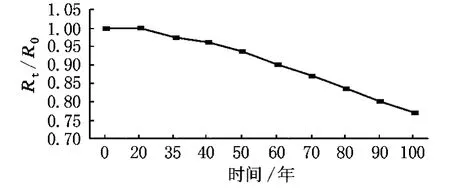
圖1 抗力時變規律曲線

圖中:R0為橋梁結構構件服役時間t=0時的抗力均值;Rt為橋梁結構構件服役時間為t時的抗力均值。

由圖1可見:橋梁結構抗力在服役期內不斷衰減,衰減速度并不均勻,初期較慢,后期較快。在服役前20年內該橋的結構抗力衰減速率為0,在后期衰減速率逐步增加。

該橋投資為28 000萬元,設計壽命為100年,拆除后價值為1 500萬元,折現率取10%。以建成時間為基期,取40年為計算周期,采用會計學的折舊模式,考慮折舊期間為30年,那么在橋齡為40年時,這部分資產已經提取完折舊,賬面殘值為0。采用基于結構可靠度的橋梁剩余價值折舊的方法,根據式(13),此時的橋梁價值為:

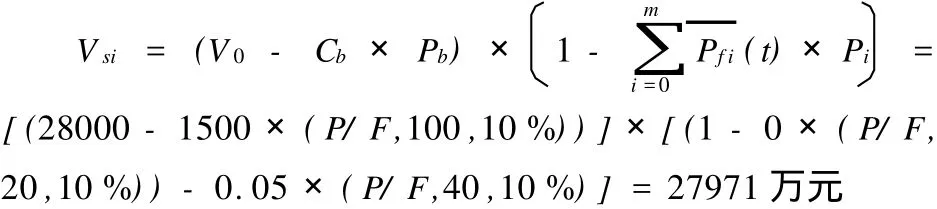
5 結語

在公共項目的評價中,經常采用的是費用收益-成本分析方法。該方法用收益-成本比率作為評價標準。一般說來,人們更關注這些公共設施給公眾帶來的收益,并建立了各種模型進行分析、預測和評價,對于成本的探討相對較少。其實公共項目的投資也要講究其投資效用比,特別是互斥方案的比選,找到比較科學的方法計算其成本更為重要。對于在路網中發揮咽喉作用的橋梁工程,利用相應的方法計算出殘余價值對運營法人轉交路政部門后的橋梁管理和評價有非常重要的意義,同時,它也是進行舊橋加固和新建橋梁方案比選決策的重要依據。

[1] 鄧平.對基礎設施固定資產折舊方法的探討[J].海南大學學報:社會科學版,1999(2):59261.

[2] 張建仁,劉揚,許福友,等.結構可靠度理論及其在橋梁工程中的應用[M].北京:人民交通出版社.2003.

[3] 趙國藩,李云貴.舊有結構性能評估[J].大連理工大學學報,199l(6):687-692.

[4] 趙國藩.貢金鑫.趙尚傳.等.工程結構生命全過程可靠度研究[M].北京:中國鐵道出版社,2001.

責任編輯:文 月

U44211

A

167128275(2010)052012422.5

2010202224

陳莘(19702),男,安徽合肥人,安徽省公路橋梁工程公司高級工程師。研究方向:路橋工程技術。