柔性吊桿張拉力的探討

許偉清

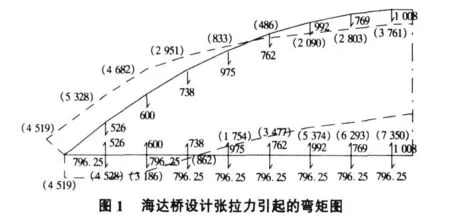
在蘇南地區下承式系桿拱橋采用柔性吊桿的,已略多于剛性吊桿的數量。由于其恒載主要是沿跨徑作用的均布荷載,所以絕大多數的拱肋軸線采用的是拋物線形。我們把海達橋的吊桿張拉力作用到系桿和拱肋上,就可以得到作用在系桿和拱肋上的恒載內力,如圖1所示。

由圖1可見,上述張拉力引起的彎矩是很大的(與以下圖4相比),甚至已失去了合理拱軸線——拋物線拱軸的力學意義。為探討其張拉力的合理性,我們以“反證”的方法:取吊桿中的張拉力為懸掛在吊桿區間內的恒載,作為吊桿張拉力。以海達橋為例,每根吊桿的張拉力為P=796.25 k N,將其加載到拱肋和吊桿上,觀察系桿和拱肋中的恒載內力。如果所取得的恒載內力遠小于圖1中的內力,那就說明柔性系桿拱橋中的張拉力,取吊桿區間的恒載作為基本張拉力是合理的,而且張拉時,操作工也便于記憶。為便于說明和理解其力學意義,這里選用“力法”對海達橋結構進行具體分析。

1 海達橋概況

海達橋上部采用86.8 m單跨預應力混凝土系桿拱橋,為剛性系桿剛性拱,計算跨徑L=85 m,拱軸線為二次拋物線,矢跨比為1/5,矢高 f=17 m,橋面總寬為19.1 m,凈寬為14 m。拱肋與系桿的混凝土均采用C55。拱肋采用等截面“I”字形截面,拱肋高1.6 m,寬1.3 m。系桿采用等截面箱梁,系桿高1.8 m,寬1.3 m,每片拱片設間距為5 m的吊桿16根,吊桿為柔性吊桿。其上部結構內力分析采用“橋梁博士”V3.0進行計算。

2 系桿拱橋吊桿張拉力的分析及內力計算

2.1 基本結構的選擇

眾所周知,系桿拱橋中,存在著四種不同性質的荷載:

1)拱肋自重引起的恒載。對于施工時在支架上分段澆筑,爾后再脫架施工的拱肋來說,由于拱肋自重引起的彎矩是很小的,同時它與吊桿張拉力無關,本文未加考慮。2)橋面自重引起的恒載內力。這部分的恒載除系梁自重可產生吊桿節間彎矩外(約占計算值的23%),其余是作用在吊桿上的節點荷載,據計算包括系梁自重在內的節點荷載為Pi=796.25 k N,我們將吊桿張拉力增大5%(但這不同于優化計算),其系桿彎矩將比原設計大8倍,所以以下的計算就取作用在吊桿上的恒載作為設計張拉力,本文將主要敘述這一觀點。3)活載內力。如果吊桿和系梁中的張拉力選擇恰當,系桿拱橋中的恒載彎矩就能削減到極小,使活載彎矩占據設計的主要部分。4)溫度變化及混凝土收縮徐變的影響,其值同樣較小。

由于本文僅對吊桿張拉力進行探討,所以以下的計算就以作用在吊桿上的恒載作為吊桿張拉力Pi=796.25 kN,進行拱肋和系梁中的內力計算。

為方便計算將作用在拱肋上的張拉力作為均布荷載:

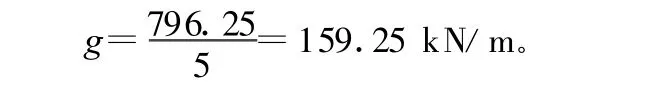
因此作用在基本結構拱肋上的靜定彎矩可寫成通式:

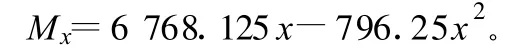
單位力x1=1作用于基本結構上的彎矩圖見圖2。

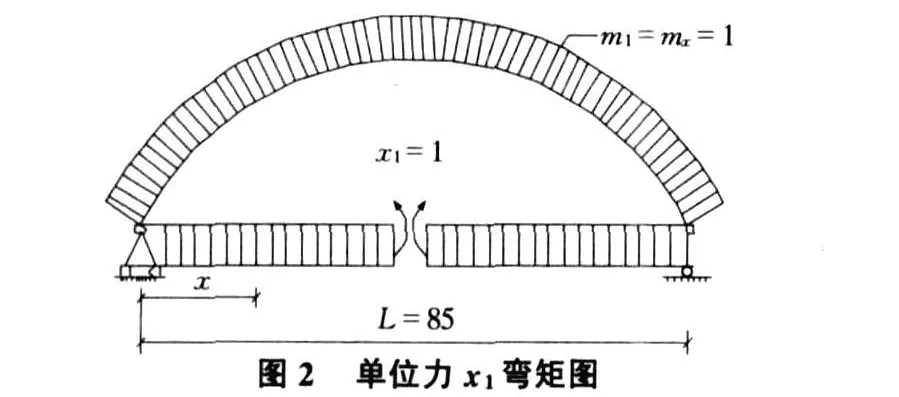
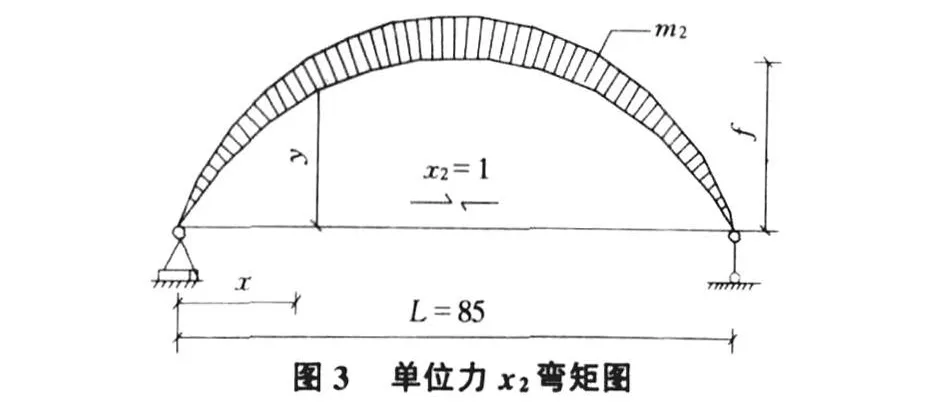
單位力x2=1作用于基本結構上的彎矩圖見圖3。

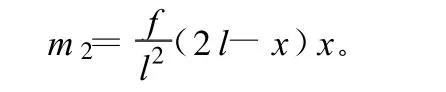
2.2 基本結構的變位計算

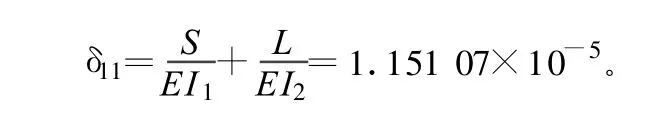
其中,S=1.103 47×85為拱肋弧長。

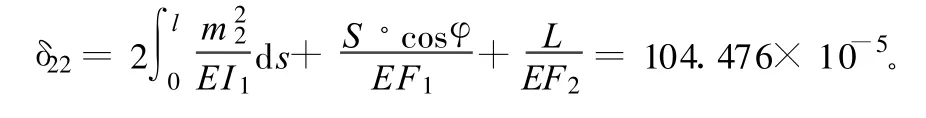
其中,φx取平均值。

2.3 結構超靜內力計算

解之得:x1=354.8 k N-m,x2=8 407.4 k N。

2.4 結構恒載內力計算

最終的恒載內力可用下式表示:

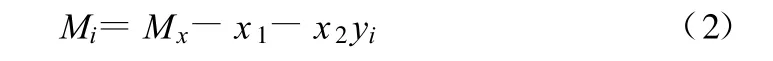
計算結果見圖4。與圖1相比較可見,由吊桿張拉力引起的結構內力差距十分巨大,顯然柔性吊桿的張拉力宜以作用在吊桿上的恒載為主來確定。

2.5 拱肋和系梁恒載彎矩的消除方法

如果我們在法方程組(1)中略去δ22中因拱肋彈性壓縮和系梁的彈性拉伸這一項,即扣除10-5,則:δ22=(104.476-0.334)×10-5=104.136×10-5。

略去公因子10-5后代入法方程組(1)中可得:

利用方程(2)計算,可以幾乎全部消除拱肋和系梁中的恒載彎矩,這就是說在以吊桿恒載作為吊桿張拉力的同時,對系梁施以8 460.15 k N的張拉力(拱肋自重引起的推力另計),便可絕大部分地消除拱肋中的恒載彎矩。

2.6 吊桿張拉力必須精確確定的必要性

如果將吊桿張拉力增加+5%,依照上面的計算可得系梁和拱肋中的彎矩圖形,與圖4相比彎矩增加了8倍。說明吊桿張拉力的微小變化,就能十分靈敏的影響拱肋和系梁的內力。故在柔性吊桿的系桿拱橋中,必須精確地確定吊桿的張拉力。

3 結語

本文提出以恒載自重作為吊桿張拉力,并結合系桿適當超張拉以消除拱肋彈性壓縮和系梁彈性拉伸的影響后幾乎可以消除拱肋和系梁中的恒載彎矩,這就基本上奠定了恒載作為吊桿張拉力的基礎。關于最終的吊桿張拉力,如果需要的話還應結合拱肋自重、活載和其他附加力的影響,作進一步的優化處理后,稍有變化還是有可能的,但張拉力決不會那么大幅度的變化。