淺析導航系統不同順序之間坐標變換的統一性
李成 安佰勇 俞利江 海軍潛艇學院學員3隊 266071
淺析導航系統不同順序之間坐標變換的統一性
李成 安佰勇 俞利江 海軍潛艇學院學員3隊 266071
列舉了在實踐中導航系統中坐標變換的常用方法,指出在方向余弦陣中,應用立體解析幾何分析,雖然旋轉角度不是矢量,不滿足平行四邊形法則,但是通過一定的變換,使每軸旋轉不同角度,則不同旋轉順序的坐標軸變換都可以得到相同的結果,即體現方向余弦陣不同順序之間的統一性。給出了一種坐標變換的思路,同時也解釋了導航坐標變換的意義在于其有實際的物理意義。
坐標變換;方向余弦陣;不同順序;統一性
1 引言
現代導航設備中不論是平臺式慣導還是捷聯式慣導,其隨著時間的推移都需要進行大量的坐標變換。旋轉矢量法在解決復雜角速度變化環境下的坐標變換問題以其有效地補償不可交換性誤差而被廣泛采用。同時,其根據不同的角速度變化情況通過改變一個周期內的采樣次數而進行的多子樣的算法和與之匹配的龍格庫塔法可以大大提高坐標系變換后的精度。而作為旋轉矢量法的單子樣的特例,四元數法在角速度變化不復雜的情況下也有著廣泛的應用,四元數法的優點在于其算法更新得快,運算量小。大多數參考書上提到方向余弦矩陣法坐標變化時都認為它的不可交換性誤差導致了有限旋轉不是矢量。而通過立體幾何的分析可知,任何一種變換順序都可以完成從起始坐標系到固定坐標系的坐標變換,而且彼此之間誤差固定在一個相差不大的數量上。同時,可以大大減少實際中的運算量。
2 變換原理
起始如下圖所示,設固定A系,經過旋轉變換到達B系,(這里忽略坐標系的平動和伸縮變換,其平動和伸縮變換可以通過在變換結果上加一個固定矢量和乘一個比例因子得到)測量兩個坐標系對應軸向之間的夾角,設定對應X軸之間的夾角為α,對應Y軸之間的夾角為β,對應Z軸之間的夾角為γ。

圖1 固定坐標系之間的對應軸向角度
先對三個夾角的范圍進行討論:由圖可知,B系的XB可以看作是以O為頂點,Z=x*tanα為母線的圓錐上的一條母線,其圓錐方程為:

設定XB軸與X軸形成的平面與YOZ平面形成的角度為θ,則可知在此XB軸的方向矢量為

同時以O點為頂點,以Y軸為軸心的圓錐方程為

通過聯立方程(2)(3)可得β角的取值范圍:

上式中,若tanβ=0,即β=0,則表示YB軸相對于Y軸沒有變化。同時取y=1,θ=π/2,得到YB軸的方向,代入ZB軸的定義式中ZB=XB×YB可得到ZB的方向為:

其中對應于YB的兩種選法,ZB有兩種對應。這樣,三個軸向都確定下來,α角可以任意選定,β角可以在范圍內任意選定,對于選定的α和β,都有固定的γ與之對應。
接下來對各個順序的坐標變換進行說明。下面以X—Y—Z的順序展開說明:其旋轉過程如下圖所示:
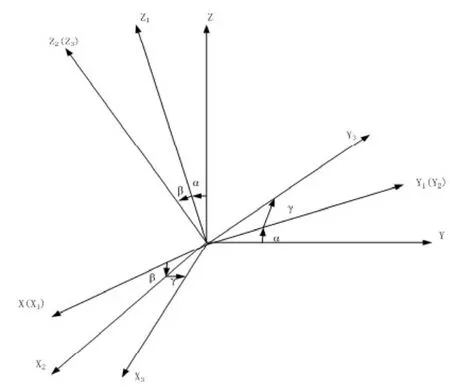
圖2 坐標系的旋轉過程
對于X軸,由三垂線定理可以知道

對于Y軸,其變化過程如下圖所示:
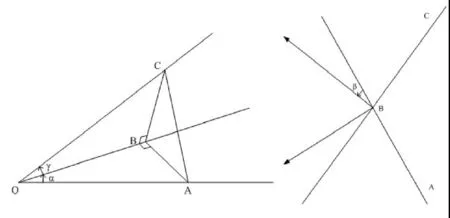
圖3 Y軸的變化過程
由三垂線定理和余弦定理可得

對于Z軸,同理可得
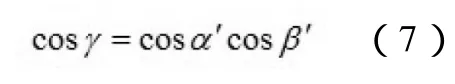
其中α’、β’、γ’分別為原坐標系繞著X、Y、Z旋轉地角度。聯立方程(5)(6)(7),就得到了關于X—Y—Z的變換順序的三個旋轉角度。

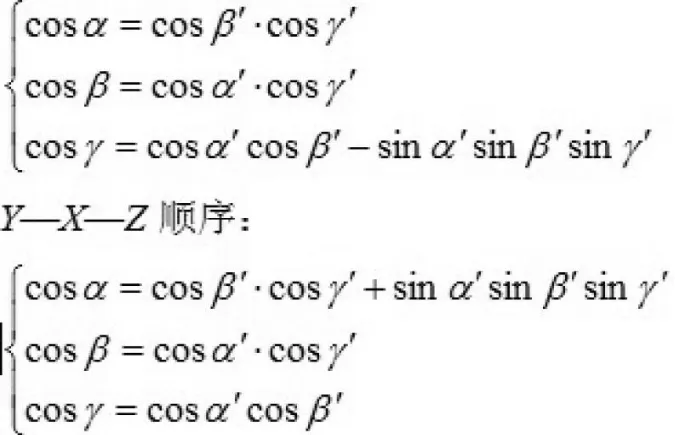
這樣,就得到了終止坐標系B系相對于A系變換后對應于六種旋轉方式的每個軸的轉量。然后通過比較一個固定的矢量如在A系的(1,1,1),來比較各種旋轉順序的誤差大小。
3 實驗仿真
通過matlab進行運算,設定初始條件下三個軸向上的對應夾角分別是α=12. 3°,β=14.6°,γ=19.1°。那么通過上面各個方程的迭代,得到如下表所示,其相對誤差的標準為取第一種變換方式,其他變換的結果與這種方式進行比較,如在試驗中,取相對誤差的標準是X—Y—Z順序的誤差限。
經過分析比較,各種變換方式其誤差相差不多,而誤差的造成主要是因為非線性三角方程時算法的誤差引入的,與其方程本身無關。
再進行大角度的比較,α=64.3°,β =87.3°,γ=52.2°,那么通過上面各個方程的迭代,得到如下表所示,同樣其誤差的標準為比較原矢量在新坐標系下沿著坐標單位矢量的投影所構成的向量。
經過分析比較,當旋轉角度比較大的時候(超過了5°角),其各種旋轉順序的結果的相對誤差依然較小。
再進行連續的比較,當坐標系B系做一個連續的變化的時候,其相對誤差隨著角度的變化的趨勢如下圖所示。

圖4 各種旋轉方式的相對誤差隨角度的變化趨勢
由上圖可知,隨著角度的增加,其相對誤差基本處于不變的狀態,而且其值趨近于零。所以,由此可以看出,各種旋轉方式在坐標旋轉的問題上可以看成是等價的。而導航系統中通常采取的Z—Y—X旋轉順序,是根據其擁有的物理意義來確定的,即航向角,縱搖角,橫搖角。
4 結束語
本文從立體解析幾何的角度出發,通過測量旋轉前后的坐標系的對應軸之間的夾角,得到不同順序下的旋轉角度,討論了不同的旋轉順序對結果的影響。在模擬仿真時,先討論了各種變化下其坐標軸夾角的取值范圍,然后根據不同的旋轉情況進行了小角度,大角度,連續情況下的探討,得到了在固定始終坐標系的情況下,不同旋轉順序在效果上時等價的。并且因為這種直接測量對應軸的角度來確定旋轉角度,進而確定坐標的方法,與坐標系的運動過程無關,只與初始最終兩個狀態量有關,而且運算量較小,其精度主要取決于非線性方程組的算法誤差,并無原理性誤差。因此可以為合適的精度下的坐標轉換方法提供一種思路。同時導航系統中通常采取的Z—Y—X旋轉順序,也是根據其擁有的物理意義來確定的,即航向角,縱搖角,橫搖角。
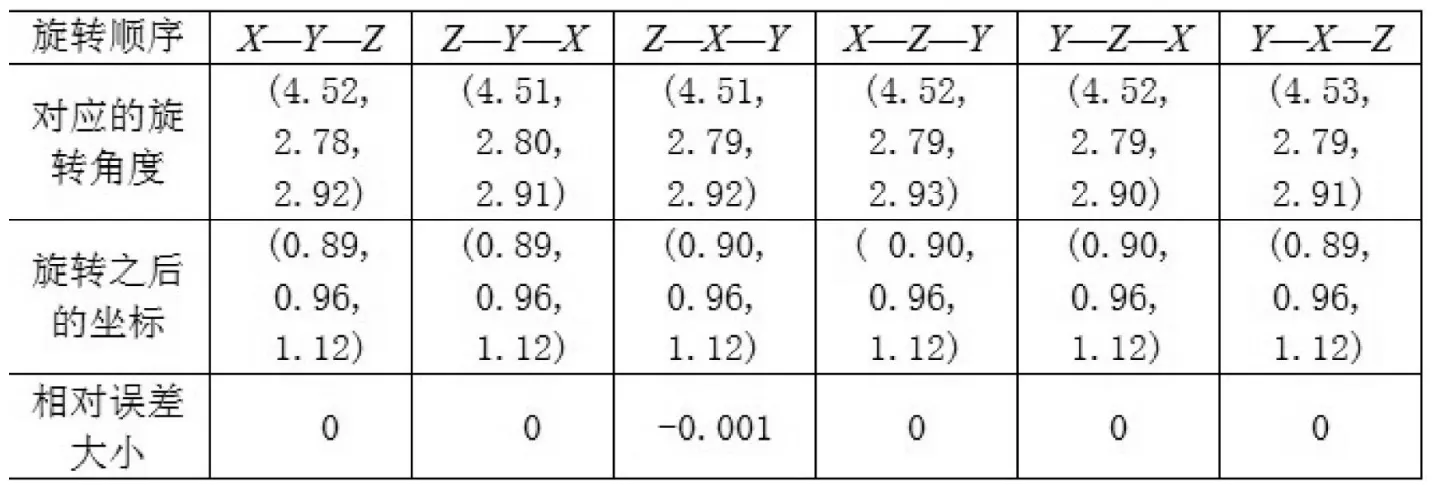
表1 小角度旋轉后各種坐標變換順序的結果和相對誤差

表2 小角度旋轉后各種坐標變換順序的結果和相對誤差
[1]劉延柱. 陀螺力學(第三版)[M]. 科學出版社.2009.
[2]陳杰. Matlab 寶典[M]. 電子工業出版社.2007.
[3]陸玨,陳義,鄭波. 總體最小二乘方法在三維坐標轉換中的應用[J]. 大地測量與地球動力學.2008年第5期,26~30頁.
[4]嚴新生.一種有效地坐標變化殘差處理法[J].測繪通報.2008年第11期,55~58頁.
[5]柯金樸.空問三維坐標轉換原理及實現[J]. 江西測繪.2008年第3期,34~37頁.
[6]陳勇.基于等效旋轉矢量法的捷聯慣導系統仿真[J].淮陰師范學院學報.2007年第4期,45~48頁.
[7]李瑩.基于飛行仿真平臺的相關坐標變換模型[J].沈陽航空工業學院學報. 2005年第4期,21~26頁.
[8]程連柱.幾種常用的GPS坐標轉換方法[J]. 計算技術與自動化.2008年第4期,16~19頁.
10.3969/j.issn.1001-8972.2010.16.152
李成(1985.08—),男,海軍潛艇學院導航、制導與控制專業在讀研究生。

