側壓系數對馬頭門圍巖應力的影響研究

李建軍

（1.太原理工大學 礦業工程學院，山西 太原 030024；2.陽泉市南煤集團大陽泉煤炭有限責任公司，山西 陽泉 045000）

側壓系數對馬頭門圍巖應力的影響研究

李建軍1，2

（1.太原理工大學 礦業工程學院，山西 太原 030024；2.陽泉市南煤集團大陽泉煤炭有限責任公司，山西 陽泉 045000）

通過三維數值模擬，研究了不同水平應力作用下馬頭門部位圍巖應力分布規律，對馬頭門的開挖及支護具有一定的理論指導意義。

側壓系數；馬頭門；數值模擬高斯函數

馬頭門（井筒與井底車場巷道相連接的部分）是礦井的咽喉部位。目前對馬頭門施工前支護問題的研究較少，大多是在馬頭門出現不穩定或破壞后如何進行馬頭門的修復。因此研究馬頭門的失穩破壞機理，對于馬頭門的施工及支護具有較高的理論價值和實際指導意義。

1 模型的建立

1 模型構建

馬頭門三維模型及計算地質網格模型，見圖1。趙固一礦風井馬頭門形狀，為大型礦井最常采用的雙面斜頂式；馬頭門位于二1煤層，頂板依次為細砂巖、中粒砂巖、砂質泥巖、泥巖與細粒砂巖互層，底板為砂質泥巖、泥巖、細砂巖、砂質泥巖等巖層。為了簡化計算，數值模擬中取厚度較大的巖層做為模擬對象，同時把厚度較小但巖性相近的巖層劃為同一層。

1.2 巖石物理力學參數選取

數值模擬過程中，巖體參數對結果的準確性有重要的影響。地質力學評價中，分析了巖體強度參數與實驗室測得巖塊強度參數之間的轉換關系，并計算出各層巖體的強度參數。

1.3 邊界條件確定

趙固一礦風井馬頭門，底板標高為-525m，埋深為608m。其中表土層厚度為526.5m，基巖厚度為81.5m。表土層平均容重為1500 kg/m3，基巖平均容重為2500 kg/m3，則圍巖應力為：σ=gγ1h1+gγ1，h1=9.94×106Pa=9.94MPa。應力施加在模型上部邊界，模型水平邊界限制x，z方向的位移；底邊為固定約束，在x，y，z三個方向上無位移。模型受力和約束，見圖3。

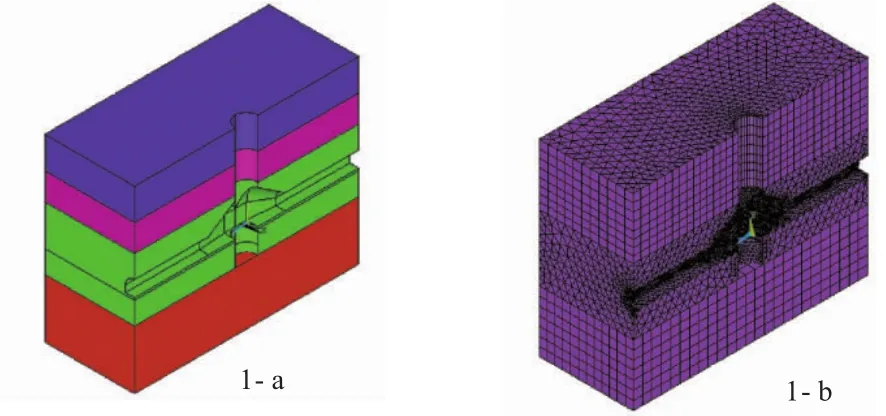
圖1 馬頭門三維模型及計算地質網絡模型

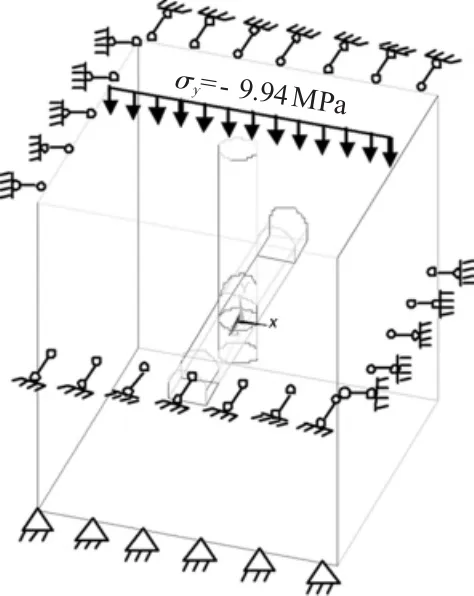
圖3 模型邊界條件

1.4 監測位置布置

為了分析馬頭門巷道的受力狀態及變形規律，沿巷道軸向，即z軸方向，在z為0、5和10m的位置布置3個測面，見圖4。現以測面2為例來分析馬頭門圍巖應力的分布。

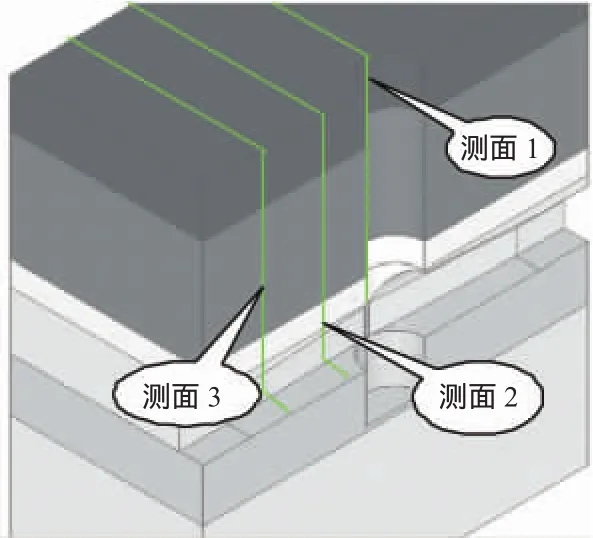
圖4 馬頭門巷道測面布置示意圖

1.5 測線的布置位置

在巷道的每個測面上布置五條測線，監測巷道底板、兩幫及頂板的受力狀態和位移變化，具體位置分別是y=-0.5，2.5，6，10m，見圖5。

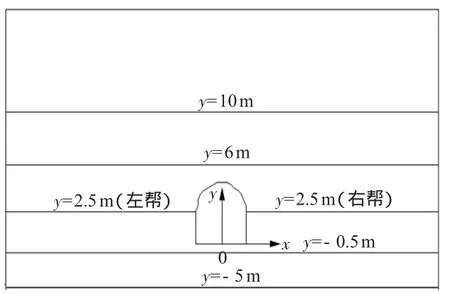
圖5 巷道測面中測線布置示意圖

2 不同側壓系數下馬頭門巷道及附近井筒應力分布規律

2.1 巷道垂直應力分布規律

圖6顯示不同側壓系數巷道測面2處垂直應力分布規律。從整體看，側壓系數不同時，測面2巷道的頂底板圍巖深部5m處，垂直應力曲線變化較大；而在巷道的頂底板附近及兩幫垂直應力曲線幾乎重合，差別不大，例如y=6，2.5，0.5三條測線所示。這說明在測面2處側壓系數的變化對巷道頂底板深部圍巖影響較大。從y=10測線看，距巷道中心0～10m的范圍內，距巷道中心距離相同的位置，垂直應力值隨λ的增大而增加；距巷道中心大于10m的范圍，距巷道中心距離相同的位置，垂直應力值隨λ的增大而減小。從y=-5測線看，距巷道中心8m位置是垂直應力值變化的分界點。從y=6，2.5，0.5三條測線看，測面2巷道頂底板附近及兩幫，垂直應力均在距巷道中心10m處達到峰值，然后應力值減小，峰值隨λ值的增大而減小。這說明測面2處巷道頂底板附近及兩幫塑性區邊界，距巷道中心10m左右。

從圖6可看出，其應力分布形態明顯呈高斯函數分布。巷道頂板10m和6m處的變化規律為：

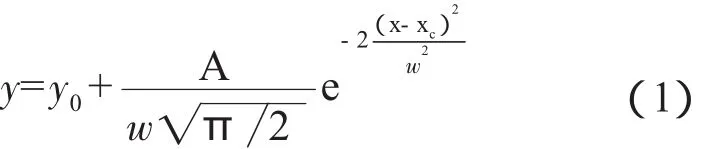
式中各參數的取值（略），xc基本上接近于0；其它各參數隨側壓系數的增大，以對數規律降低。

2.2 巷道水平應力分布規律

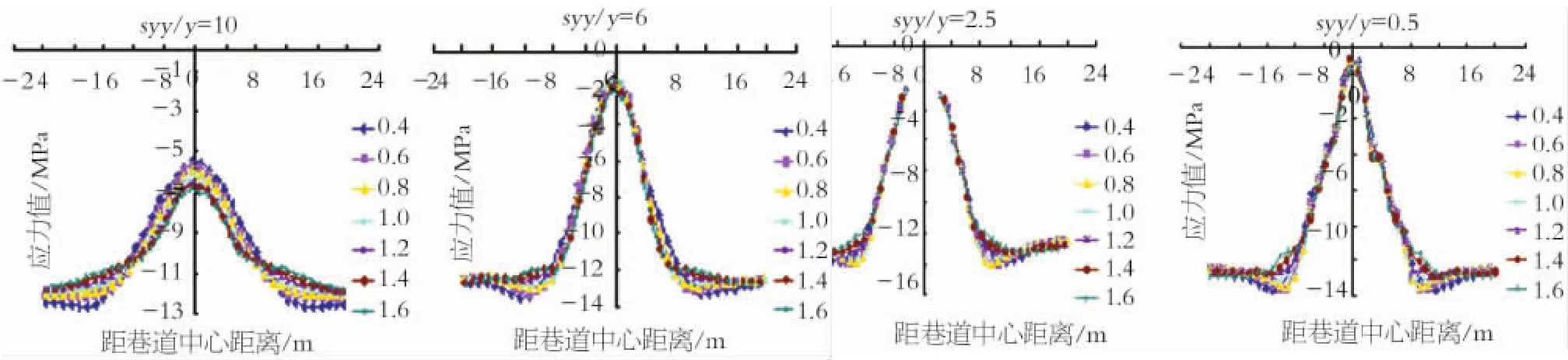
圖6 巷道測面2處垂直應力分布

施加在模型上的豎直應力為9.94MPa，當λ值分別為0.4，0.6，0.8，1，1.2，1.4，1.6時，相應初始化在模型上的水平應力為3.976，5.964，7.952，9.94，11.928，13.916，15.904MPa。

圖7顯示不同側壓系數巷道測面2處水平應力分布規律。從y=10和y=-5測線看出，水平應力峰值隨著λ值的增大而增大，且應力集中系數越來越大。從y=6和y=-0.5測線可以看出，在巷道頂板出現應力降低區，當入值從0.4增大到1時，應力降低區邊緣位置從距巷道中心3 m增至20 m，當λ＞1時，測線上點都處于應力降低區內。這說明隨著λ值的增大，巷道頂底板塑性區沿徑向不斷擴大，造成水平應力峰值不斷向圍巖深部轉移。從y=2.5測線看出，隨著λ值的增大，在兩幫水平應力峰值沿巷道徑向向圍巖深部轉移。

2.3 巷道剪切應力分布規律

圖8顯示不同側壓系數巷道測面2處剪切應力分布規律。在y=10上曲線幾乎重合，峰值不隨λ值的增加而變化，位置在距巷道中心6m左右，說明λ值的變化對測面2處巷道頂板深部圍巖剪應力及峰值位置的影響不大。由y=-0.5測線知，剪應力底板的分布與在頂板的分布相反。峰值隨λ值的增加而增大，位置在距巷道中心6m，這說明λ值的變化只影響測面2處巷道頂板深部圍巖剪應力值的大小，不影響峰值的位置。

圖7 巷道測面2處水平應力分布

圖8 巷道測面2處剪切應力分布

3 結論

通過對不同側壓系數對馬頭門圍巖應力分布規律的研究，得出如下結論：馬頭門上方垂直應力分布呈高斯函數分布，其影響范圍為距巷道中心線約±10m。越靠近馬頭門，其上方應力變化幅度越大；水平應力的影響范圍為距巷道中心線±6m，頂板上方不同層位上表現出不同的變化趨勢，遠離巷道應力升高，而靠近馬頭門則出現應力降低區；剪應力分布在頂板10m處幾乎不受巷道開挖的影響，頂板6m處則出現明顯的變化，而巷幫位置上影響最大，出現無規律的跳躍。

Study on the Influence of the Ingate Surrounding Rock by Horizontal Stress Coefficient

LI Jian-jun1，2
（1.Taiyuan University of Technology,Taiyuan Shanxi 030024;2.Dayangquan Mine,Yangquan Shanxi 045000,China）

Using3D-numerical simulation,this article study on the distribution of the stress of surrounding rock of the ingate under different horizontal stress coefficient.The research has some theory significance for the excavation and supporting of the ingate.

horizontal pressure coefficient;ingate;numerical simulation;gauss function

TD315+.1

A

1672-5050（2010）03-0046-03

2009-11-18

李建軍（1973—），男，山西孝義人，在讀工程碩士研究生，工程師，從事礦山安全監測監控工作。

徐樹文