一維緊鄰時間隨機環境下可逗留隨機游動的有關性質
宋明珠
(銅陵學院教務處,安徽銅陵 244000)
一維緊鄰時間隨機環境下可逗留隨機游動的有關性質
宋明珠
(銅陵學院教務處,安徽銅陵 244000)
給出了可數狀態空間中時間隨機環境下可逗留隨機游動的一個統一模型,對于一維緊鄰時間隨機環境下的隨機游動,在一定的條件下,討論它的極限性質和中心極限定理,該結論類似于空間隨機環境下的隨機游動的有關結論.
時間隨機環境;隨機游動;極限定理;中心極限定理
1 引言與定義
自從Solomem[1]最早引入一維獨立空間隨機環境下隨機游動的概念以來,該理論一直是人們熱點研究的問題.Kalicow[2]給出了該隨機游動在d維,一般環境下的統一模型,并得到了其常返暫留準則.近年來出現了一大批有關該模型下的隨機游動的各種極限理論,Zetouni[3]參考前人的結果,整理成一套完整的體系,其內容包括常返暫留準則、強大數定律、中心極限定理、大偏差原理等.在該理論完善的同時,Cogburn[4]和Orey[5]等人發展了另一類隨機環境下的馬氏鏈的理論,與Zetouni[3]中空間隨機環境不同的是,他們討論的是時間隨機環境.本文在前人的基礎上給出了一維緊鄰時間隨機環境下隨機游動(簡稱時間RWIRE)的統一模型,并在一定條件下,給出其相關性質.
時間RWIRE的定義主要包括兩個方面的內容:首先是環境,它是隨著時間的推移而得到的一列隨機變量,但不隨空間位置的變化而變化;其次是在給定的環境下隨機游動的轉移概率由環境決定的非齊次馬氏鏈.現在考慮其統一的模型.對任何正整數i∈,令Ui表示X上支撐為V的概率全體,其中X為可數空間,V?X.稱Ui中任一元素為時刻i的轉移律,它指的是一個函數ρi:X→[0,1]且滿足
(a)ρi(x)≥0,?x∈V;
(b)ρi(x)=0,?x?V;
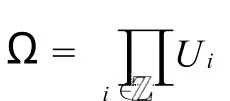
對任意的w∈Ω,定義在時間環境w下的隨機游動Xn,n≥0是以X為狀態空間,轉移概率為下式決定的隨機變量序列:
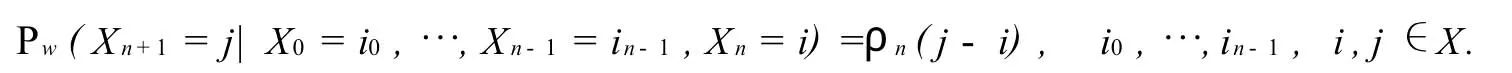
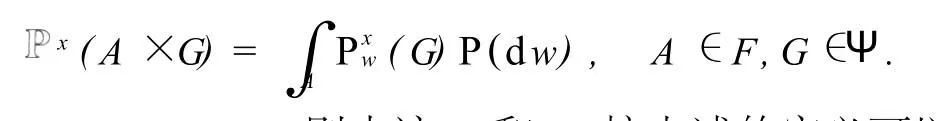
現令X=Z,Z為整數,V={-1,0,1},則由該X和V,按上述的定義可以得到一個時間隨機游動,稱此時間RWIRE為一維緊鄰時間RWIRE,即對環境w={(αn,γn,βn),n≥0},有
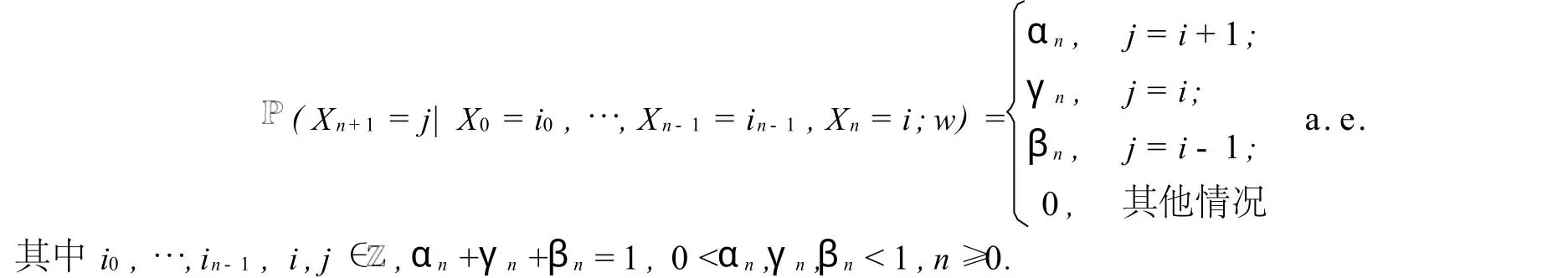
在給定的環境下,Xn,n≥0為非齊次的馬氏鏈,其轉移概率依賴于最近的位置和環境,而環境只與時間有關.
以下恒設Xn,n≥0是一維緊鄰的時間RWIRE.
2 極限性質的證明
令Tn=min{k≥0;Xk=n},τn=Tn-Tn-1,n≥1,T-n,τ-n定義類似.
引理1 若對幾乎所有的環境,Xn,n≥0在此環境下某一性質成立,則一維緊鄰時間RWIRE幾乎必然具有此性質.


3 中心極限定理的證明
引理5[8]設環境ω關于P是獨立同分布的,
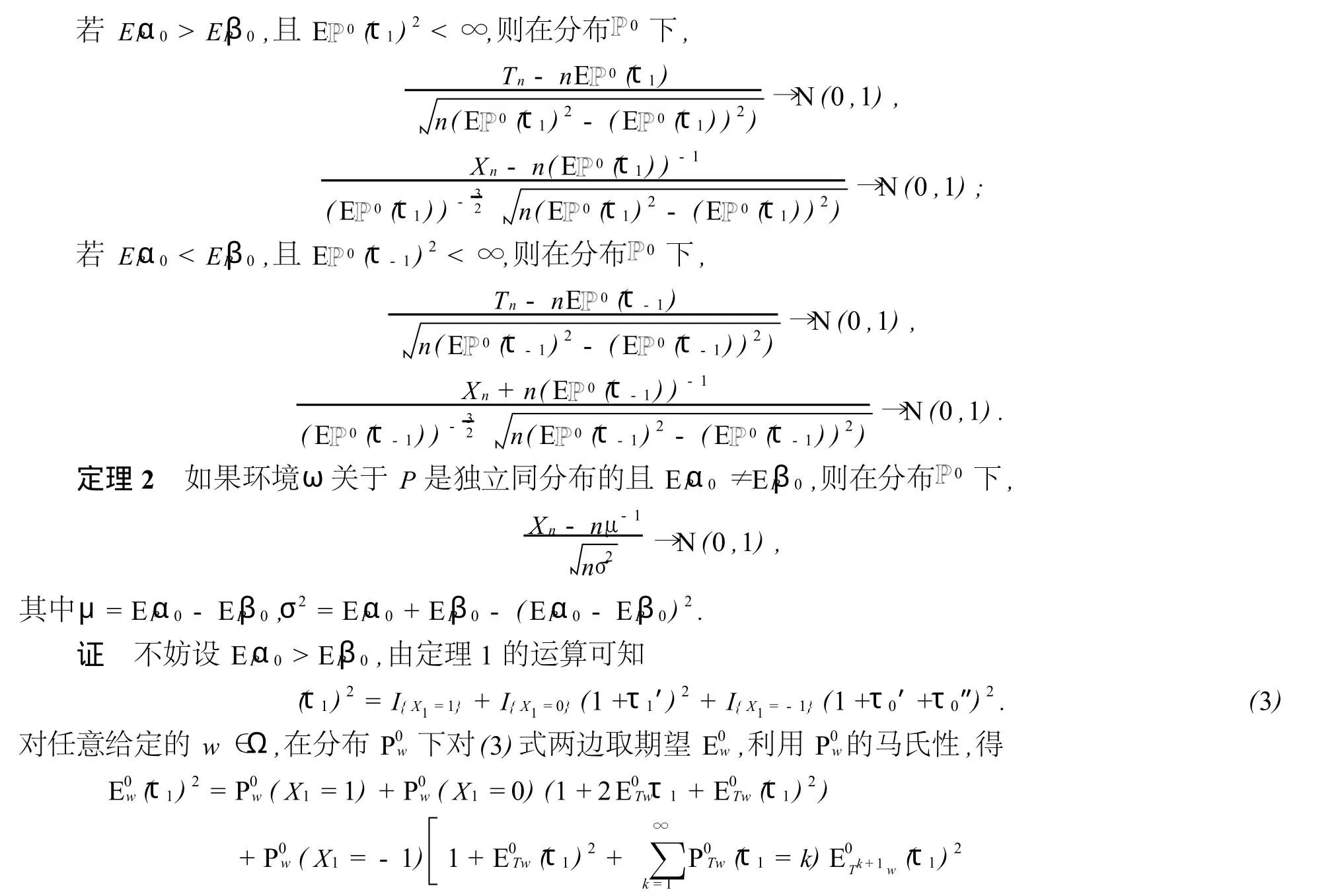

[1] Solomon F.Random walks in random enviroment[J].Ann.Prob.,1975,3(1):1-31.
[2] Kalikow S.A generalized random walks in random environments[J].Ann.prob.,1981,9:735-768.
[3] Zetonui O.Lecture notes on RWRE[DB].2001,available at http:www.wee.technion.ac.il/aeitouni/ps/notesl.ps.
[4] Cogburn R.The ergodic tehory of Markov chains in random environments[J].Z.Wahrsch.Verw.Gebiete.,1984, 66(2):109-128.
[5] Orey S.Markov chains with stochastically transtion probabilities[J].Ann.prob.1991,19(3):907-928.
[6] 張曉敏,等.時間隨機環境下的隨機游動的漸進行為[J].應用數學,2004,17(2):295-300.
[7] Stone C J.The growth of a random walk[J].Ann.Math.Statist.,1969,40:2203-2206.
[8] 吳文忠.隨機環境中一維緊鄰隨機游動的極限性質[D].安徽師范大學,2005.
Some Properties for One-dimensional Nearest-neighbor Random Walks in Time-Random Environments
SON G Ming-zhu
(Educational Administration Office of Tongling University,Tongling,Anhui 244000,China)
A general model of random walk in time-random environments in any denumerable space is given in this paper,in the case of one-dimensional nearest-neighbor random walk,we derive limit theorem and acenter limit theorem of this random walk under some conditions,which are similar to the corresponding results in the case of classical random walk.
time-random environments;random walks;limit theorem;center limit theorem
O211.62
A
1672-1454(2010)03-0084-04
2007-09-04;[修改日期]2008-02-29
銅陵學院院級科研項目(2009tlxy23)

